Доверительная вероятность и доверительный интервал

Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра.

Для практики важно не только получить точечную оценку, но и определить интервал, называемый доверительным, между границами которого с заданной доверительной вероятностью находится истинное значение оцениваемого параметра.

P {x_н < x < x_в} = (1-q).

где q — уровень значимости; х_н, х_в — нижняя и верхняя границы интервала разброса Х.

В общем случае доверительные интервалы можно строить на основе неравенства Чебышева. При любом законе распределения случайной величины, обладающей моментами первых двух порядков, верхняя граница вероятности попадания отклонения случайной величины х от центра распределения Х_ц интервал tS_x описывается неравенством Чебышева.

P {|xX_ц|? tS_x}? (1 — 1/ t²).

где S_x — оценка СКО распределения; t — положительное число.

Для нахождения доверительного интервала не требуется знать закон распределения результатов наблюдений, но нужно знать оценку СКО.

Полученные с помощью неравенства Чебышева интервалы оказываются слишком широкими для практики. Так, доверительной вероятности 0,9 для многих законов распределений соответствует доверительный интервал 1,6S_x. Неравенство Чебышева дает в данном случае 3,16S_x. В связи с этим оно не получило широкого распространения.

В метрологической практике используют главным образом квантильные оценки доверительного интервала. Под 100*P-процентным квантилем (х_р) понимают абсциссу такой вертикальной линии, слева от которой площадь под кривой плотности распределения равна Р%. Иначе говоря, квантиль — это значение случайной величины (погрешности) с заданной доверительной вероятностью Р. Например, медиана распределения является 50%-ным квантилем — х₀₅.

На практике 25- и 75%-ный квантили принято называть сгибами, или квантилями распределения. Между ними заключено 50% всех возможных значений случайной величины, а остальные 50% лежат вне их.

Интервал значений случайной величины х между x_0.05 и x_0.95 охватывает 90% всех ее возможных значений и называется интерквантильным промежутком с 90%-ной вероятностью. Его протяженность равна.

d_0.9 = x_0.95 — x_0.05

На основании такого подхода вводится понятие квантильных значений погрешности, т. е. значений погрешности с заданной доверительной вероятностью Р — границ интервала неопределенности.

±?_Д = ±(х_р-х_1-р}/2 = ±d_р/2.

На его протяженности встречается Р% значений случайной величины (погрешности), а q = (1-P)% общего их числа остаются за пределами этого интервала.

• 1) Для получения интервальной оценки нормально распределенной случайной величины необходимо:
  • * определить точечную оценку МО () и СКО (S_x) случайной величины по формулам (8) и (11) соответственно;
  • * выбрать доверительную вероятность Р из рекомендуемого ряда значений 0,90; 0,95; 0,99;

F (x_н) = q/2 = (1 — P)/2; F (x_в) = (1 — q/2) = P + q /2.

* найти верхнюю х_в и нижнюю х_н границы.

Значения х_н и х_в определяются из таблиц значений интегральной функции распределения А (t) или функции Лапласа Ф (t).

Полученный доверительный интервал удовлетворяет условию.

где n — число измеренных значений;

z_p — аргумент функции Лапласа Ф (t), отвечающей вероятности Р/2.

В данном случае z_p называется — квантильным множителем.

Половина длины доверительного интервала D_р = z_pS_x/n^½ называется доверительной границей погрешности результата измерений.

Пример 1.

Произведено 50 измерений постоянного сопротивления. Определить доверительный интервал для МО значения постоянного сопротивления, если закон распределения нормальный с параметрами.

m_x = = 590 Ом,.

S_x = 90 Ом при доверительной вероятности Р = 0,9.

Так как гипотеза о нормальности закона распределения не противоречит опытным данным, доверительный интервал определяется по формуле.

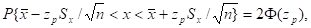
Ф (z_р) = Р/2 = 0,45.

z_p= 1,65.

Следовательно, доверительный интервал запишется в виде.

(590 — 1,65 *90/50^½) < R < (590 + 1,65 * 90 / 50^½) или (590−21) < R < (590+21). Окончательно 569 Ом < R < 611 Ом.

При отличии закона распределения случайной величины от нормального необходимо построить его математическую модель и определять доверительный интервал с ее использованием.

Рассмотренный способ нахождения доверительных интервалов справедлив для достаточно большого числа наблюдений n, когда у = S_x. Следует помнить, что вычисляемая оценка СКО S_x является лишь некоторым приближением к истинному значению у.

Определение доверительного интервала при заданной вероятности оказывается тем менее надежным, чем меньше число наблюдений.

Нельзя пользоваться формулами нормального распределения при малом числе наблюдений, если нет возможности теоретически на основе предварительных опытов с достаточно большим числом наблюдений определить СКО. .

2) Расчет доверительных интервалов для случая, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна, т. е. при малом числе наблюдений n, возможно выполнить с использованием распределения Стьюдента S (t, k). Оно описывает плотность распределения отношения (дроби Стьюдента):

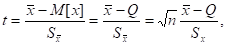
где Q — истинное значение измеряемой величины. Величины, и вычисляются на основании опытных данных и представляют собой точечные оценки: МО, СКО среднего арифметического значения и СКО результатов измерений.

= / n^½

Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (-t_p; +t_р).

t_p — называется коэффициентом Стьюдента.

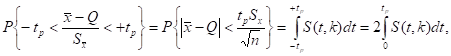
где k — число степеней свободы, равное (n — 1). Величины t_p (называемые в данном случае коэффициентами Стьюдента), рассчитанные с помощью двух последних формул для различных значений доверительной вероятности и числа измерений, табулированы. Следовательно, с помощью распределения Стьюдента можно найти вероятность того, что отклонение среднего арифметического от истинного значения измеряемой величины не превышает .

В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной. Распределение Стьюдента применяют при числе измерений n < 30, поскольку уже при n = 20, …, 30 оно переходит в нормальное и вместо уравнения можно использовать уравнение.

Результат измерения записывается в виде.

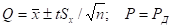
где Р_д — конкретное значение доверительной вероятности.

Множитель t при большом числе измерений (n) равен квантильному множителю z_р. При малом n он равен коэффициенту Стьюдента.

Полученный результат измерения не является одним конкретным числом, а представляет собой интервал, внутри которого с некоторой вероятностью Р_д находится истинное значение измеряемой величины. Выделение середины интервала вовсе не предполагает, что истинное значение ближе к нему, чем к остальным точкам интервала. Оно может быть в любом месте интервала, а с вероятностью 1-Р_д даже вне его.

Пример 2.

Определение удельных магнитных потерь для различных образцов одной партии электротехнической стали марки 2212 дало следующие результаты: 1.21; 1.17; 1,18; 1,13; 1,19; 1,14; 1,20 и 1,18 Вт/кг.

Считая, что систематическая погрешность отсутствует, а случайная распределена по нормальному закону, требуется определить доверительный интервал при значениях доверительной вероятности 0,9 и 0,95. Для решения задачи использовать формулу Лапласа в распределении Стьюдента.

1) По формулам находим оценки среднего арифметического значения и СКО результатов измерений.

Они соответственно равны = 1,18 и S_x = 0,0278 Вт/кг.

Считая, что оценка СКО равна самому отклонению, находим:

Отсюда, используя значения функции Лапласа, приведенные в таблице приложения 1, определяем, что z_р = 1,65 (для Р = 0,9).

Для Р = 0,95 коэффициент 2-й z_p = 1,96.

Доверительные интервалы, соответствующие Р = 0,9 и 0,95, равны 1,18±0,016 Вт/кг и 1,18±0,019 Вт/кг.

2) В том случае, когда нет оснований считать, что СКО и его оценка равны, доверительный интервал определяется на основе распределения Стьюдента:

По таблице в приложении 2 находим, что t_0.9 = 1,9 и t_0.95 = 2,37.

Отсюда доверительные интервалы соответственно равны 1,18±0,019 Вт/кг и.

1,18±0,023 Вт/кг.