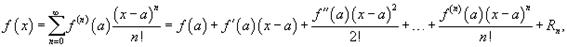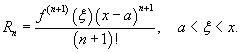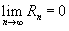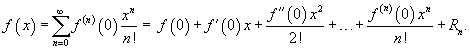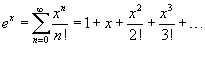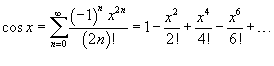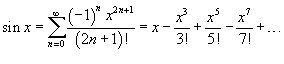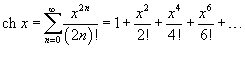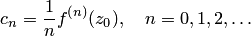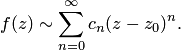Ряд Тейлора, Маклорена

Если функция f (x) имеет непрерывные производные вплоть до (n+1)-го порядка, то ее можно разложить в степенной ряд по формуле Тейлора:

где R_n? остаточный член в форме Лагранжа определяется выражением.

Если приведенное разложение сходится в некотором интервале x, т. е., то оно называется рядом Тейлора, представляющим разложение функции f (x) в точке a.

Если a = 0, то такое разложение называется рядом Маклорена:

Разложение некоторых функций в ряд Маклорена.

Теорема Тейлора о разложении функции в степенной ряд

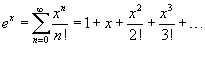
Теорема. Функция, аналитическая в области, в окрестности каждой точки этой области представляется в виде степенного ряда, радиус сходимости которого не меньше, чем расстояние от точки до границы области .

На основании теоремы можно сформулировать алгоритм решения поставленной выше задачи и вывод — утверждение.

Алгоритм разложения аналитической функции в степенной ряд.

1. Найти производные от данной функции:

.

2. Вычислить значения производных в точке; записать коэффициенты по формуле. Составить ряд по степеням с этими коэффициентами, который соответствует данной функции.

3. Найти область сходимости полученного ряда и записать разложение.

Если функция не имеет конечных особых точек, то ряд сходится к ней во всей плоскости, .