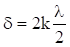Интерференция света. 
Волновая оптика

Интерференцией света называется наложение световых волн, сходящихся в одной точке, при котором происходит их взаимное усиление в одних точках пространства и ослабление в других. Необходимым условием интерференции волн является их когерентность. Когерентными называют такие волны, у которых разность фаз возбуждаемых ими колебаний в данной точке пространства остается постоянной во времени. Синусоидальные волны, частоты которых одинаковы, когерентны всегда.

Монохроматическая волна — это строго синусоидальная волна с постоянными во времени частотой н и щ = 2рн, амплитудой, А и начальной фазой ц₀. Амплитуда и фаза колебаний могут меняться от одной точки пространства к другой, а частота колебаний одна и та же во всем пространстве.

Реальная волна не является, строго говоря, монохроматической. Спектр ее частот имеет конечную ширину Дщ, т. е. включает циклические частоты от: щ — до щ + .

Такую волну можно приближенно рассматривать как монохроматическую с циклической частотой щ в течение ограниченного промежутка времени Дt много меньшем чем .

Величину:

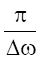
= ф_ког

называют временем когерентности монохроматической волны. Как понимать время когерентности?

За время ф_ког разность фаз колебаний, соответствующих волнам с частотами в пределах от щ — до щ +, изменяется на р.

Волна с циклической частотой и фазовой скоростью v за это время распространяется на расстояние:

l_ког = v ф_ког = v,.

называемое длиной когерентности или длиной гармонического цуга, соответствующего рассматриваемой негармонической волне.

Чем ближе данная волна к монохроматической, тем меньше Дщ и тем больше ф_ког и l_ког.

Так для видимого солнечного света, имеющего сплошной спектр частот от 4· 10¹⁴ до 8· 10¹⁴ Гц, ф_ког 10^-14с и l_ког 10^-6м. Для лазеров непрерывного действия ф_ког 10^-5с, l_ког 10-³м.

Когерентность колебаний, которые совершаются в один и тот же момент времени в разных точках плоскости Q, перпендикулярной направлению распространения волны, называют пространственной когерентностью (в отличие от временной, когда колебания совершаются в одной и той же точке пространства, но в разные моменты времени).

Пространственная когерентность зависит от условий излучения и формирования волн. Например, световая волна, излучаемая точечным источником, обладает полной пространственной когерентностью. В случае идеальной плоской волны амплитуда и фаза колебаний во всех точках плоскости Q одинаковы, т. е. также имеется полная пространственная когерентность. Пространственная когерентность сохраняется по всему поперечному сечению пучка света от лазера.

В реальной волне, излучаемой множеством независимых атомов протяженного (неточечного) источника, разность фаз Дц в двух точках К ₁ и К ₂ на плоскости Q, — будет случайной функцией времени. В качестве длины пространственной когерентности принимают расстояние l_к между точками К₂ и К₁ плоскости Q, случайные изменения разности фаз в которых достигают значения равного р. Площадь круга радиусом l_к называется размером пространственной когерентности, а цилиндр на этом круге с образующей, равной длине гармонического цуга называется объемом пространственной когерентности.

Пусть две волны одинаковой частоты щ, накладываясь друг на друга, возбуждают в некоторой точке пространства колебания одинакового направления, описываемые следующими выражениями:

A₁ cos (щt + ц₁).

A₂ cos (щt + ц₂),.

где А₁ и А₂ — амплитуды, ц₁ и ц₂ — начальные фазы колебаний. Амплитуда результирующего колебания, А будет определяться из выражения, А ² = А ²₁ + А ²₂ + 2А ₁А ₂ cos (ц₂ — ц₁).

Если разность фаз Дц = ц₂ — ц₁ остается постоянной во времени, то волны будут когерентными. В случае некогерентных волн разность фаз ц₂ — ц₁ непрерывно меняется, принимая с равной вероятностью любые значения, вследствие чего среднее по времени значение cos (ц₂ — ц₁) равно нулю. И тогда:

² = 1>² + 2>².

Это значит, что интенсивность света, наблюдаемая при наложении некогерентных волн, равна сумме их интенсивностей в каждой точке пространства.

В случае когерентных волн cos (ц₂ — ц₁) имеет постоянное значение в каждый момент времени (но свое для каждой точки пространства), так что амплитуда будет определяться из выражения:

А² = А²₁ + А²₂ + 2А ₁А ₂ cos (ц₂ — ц₁).

В тех точках пространства, где:

cos (ц₂ — ц₁) > 0,.

A²? A²₁ + A²₂,.

cos (ц₂ — ц₁)? 0, там A²? A²₁ — A²₂.

Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других минимумы интенсивности. Особенно отчетливо это проявляется в случае, когда амплитуды колебаний равны, А ₁ = А ₂.

Условия максимума и минимума при интерференции волн света можно сформулировать через разность фаз Дц и через разность хода двух волн д.

1. а) Если разность фаз равна четному числу р:

Дц = ц₂ — ц₁= 2кр, (к = 0,1,2,…),.

cos (ц₂ — ц₁) = 1.

А = А ₁ + А ₂

• — это условие максимума.
• б) Если разность фаз равна нечетному числу р:

Дц = (ц₂ — ц₁) = =(2к + 1) р, (к = 0,1,2,…),.

cos (ц₂ — ц₁) =-1.

А = А ₁ — А ₂

• — это условие минимума.
• 2. Известно, что разности фаз Дц = р соответствует пройденный волной путь, равный. С учетом этого:
  • а) если разность хода двух волн, равна четному числу полуволн:

.

то наблюдается усиление интенсивности света, т. е.

А = А ₁ + А ₂

• — это условие максимума,
• б) если разность хода двух волн, равна нечетному числу полуволн:

.

то наблюдается уменьшение интенсивности света, т. е.

А = А ₁ — А ₂

— это условие минимума.

В случае, когда, А ₁ = А ₂, амплитуда результирующего колебания, А равна нулю и в точке схождения двух волн света не будет.

При изучении оптических явлений различают геометрическую L и оптическую l длину пути или хода волн, которые связаны между собой соотношением:

l = Ln,.

где n — показатель преломления среды, в которой распространяется свет.