Комбинаторные задачи в программном содержании курса математики начальной школы

История включения комбинаторных задач в школьный курс математики.

В середине 70-х годов в программное содержание младшей ступени средних школ Японии, наряду с разделами «Числа и алгебраические выражения», «Функции»,.

«Геометрические фигуры», был включен раздел «Вероятность и статистика». В процессе изучения данного раздела японские школьники учатся целенаправленно собирать данные, располагать их в виде таблиц, чтобы усмотреть закономерность в их поведении.

В американских школах в содержательную часть стандарта (1989г.) начальной школы (1−4 классы) включен раздел «Элементарные основы статистики и вероятностей»; средней ступени (5−8 классы) — «Статистика и вероятность», старшей школы (9−12 классы) ;

«Статистика. Вероятность. Дискретная математика».

Во французских школах большое значение уделяется изучению теории вероятностей и статистики, которая не содержит ни формальной теории, ни технически сложных задач. Все понятия в этом курсе вводятся естественным образом при рассмотрении соответствующих примеров из реальной жизни, задачи решаются неформальными способами, то есть преподавание ведется на доступном ученику уровне.

В 1973 году венгерский ученый Томас Варга доказал в своих экспериментальных исследованиях, что ученики начальных классов способны решать комбинаторные задачи. Более чем в ста школах Венгрии им был проведен эксперимент по обучению младших школьников начальным понятиям вероятности и комбинаторики. Результатом данного эксперимента стало убеждение автора в том, что идея обучения комбинаторике и теории вероятностей может быть реализована в начальной школе.

Вопрос о включении комбинаторных, вероятностных и статистических задач в школьный курс математики рассматривался неоднократно, в России данный вопрос ставился с середины 19 века, что было обусловлено идеями и периодами реформирования математического образования.

Целесообразность включения элементов комбинаторики, теории вероятности и математической статистики рассматривали такие выдающиеся математики, как А. Н. Колмогоров, А. Я. Хинчин, С. Н. Бернштейн, Б. В. Гнеденко, это обосновывалось необходимостью систематического развития у учащихся идеи наличия в природе закономерностей более широкой природы, а именно статистических закономерностей.

А.Н. Колмогоров разработал возможные подходы к изложению понятия вероятности для факультативного курса в старших классах, а также содержание и методику самого курса, также высказал надежду, что «этот материал в значительной своей части в будущем войдет в основной школьный курс математики. Желательно, чтобы при ведении факультативных занятий в школах выработалась определенная традиция его изложения, которая потом могла бы быть перенесена на работу со всеми учащимися».

В 1967 году в факультативный курс X класса были включены следующие вопросы:

Начала комбинаторики и вычисление вероятностей при помощи подсчета числа благоприятствующих случаев.

Операции над событиями, теорема сложения вероятностей, условные вероятности и независимость событий.

Независимые повторные испытания с постоянной вероятностью, теорема Бернулли (без доказательства), заключительная беседа о различных областях науки и практической деятельности.

Попытки изложения для школьников основных идей теории вероятностей были предприняты И. Г. Журбенко. Построить отдельный курс основ теории вероятностей предлагали Б. В. Велиев, И. М. Гайсинская, В. Г. Потапов.

Выделению вероятностно-комбинаторной линии в школьном курсе математики посвящены исследования Л. М. Кабековой, А. Я. Дограшвили, З. П. Самигулиной, Л.Бычковой. В работах данных авторов приводятся аргументы в пользу совместного изучения элементов комбинаторики и теории вероятностей, связанных как обособленностью элементов комбинаторики от других тем, так и особенностью их содержания. В связи с этим, на усвоение комбинаторики тратится много времени, что не позволяет глубоко изучить вопросы теории.

По мнению Л. М. Кабековой, изучение элементов комбинаторики внутри раздела «Элементы теории вероятностей» позволит отказаться от решения искусственных задач по комбинаторике и тем самым сэкономить время для более глубокого курса теории вероятностей. Этот путь дает возможность комбинаторику — самостоятельную область математики со своими задачами и со своими методами — рассматривать как составную часть теории вероятностей с вероятностными выводами основных формул. При этом учащиеся знакомятся и с комбинаторными методами.

А.Я. Дограшвили полагал, что задачи вероятностного и комбинаторного характера разбросаны по всему курсу математики восьмилетней школы и не приведены в систему[14]. В его работе, которая посвященная формированию у учащихся восьмилетней школы умений и навыков решения комбинаторных задач, была предпринята попытка привести задачи комбинаторного и вероятностного характера к определенному единству по классам и создать определенную систему задач указанного типа соответствующую действующей в то время программе по математике. Основу этой системы составляют этапы, учитывающие, прежде всего возрастные особенности учащихся.

Автор полагает, что в классах уровень знания учащихся в указанном направлении определяется тем, что не превышает их сферу чувств. В старших же классах от учеников требуется уже логическое мышление, которое опирается на метод неполной индукции: ученики высказывают гипотезы, а затем производят их проверку.

Изучение понятий комбинаторики и теории вероятностей в четвертом классе согласовано с изучением множеств, при этом процесс делится на два этапа. На первом рассматривается одно множество, содержащее небольшое число элементов, устанавливается связь между количеством элементов и количеством выделенных пар. На втором этапе рассматриваются два разных множества, содержащие малое число элементов, и составленные из них всевозможные пары.

В четвертом и пятом классах учащиеся уже решают комбинаторно-вероятностные задачи, используя предложенные правила, закрепляют знания пройденного материала по вопросам: множества, часть и дроби, их свойства, отрезок, луч, ломаная и т. д. В шестом классе ученики пользуются для решения комбинаторных задач уже известными им правилами. Задачи, требующие применения общих формул, автор предлагает включить в 7−8 классы.

Большинство исследований того времени были адресованы теории вероятностей и комбинаторики, в меньшей степени рассматривались элементы математической статистики. Несмотря на большое количество разработок, раздел «Элементы комбинаторики и теории вероятностей» был исключен из проекта программы общеобразовательных школ, предлагаемые экспериментальные программы использовались как факультатив, либо в специальных классах с углубленным изучением математики.

В последующие годы, в связи с потребностями смежных дисциплин, постепенно стал проявляться акцент на усиление практической и прикладной направленности вероятностно-статистического материала.

Новый этап исследований, связанный с возможностью включения комбинаторных и вероятностных задач в программу отечественной общеобразовательной школы, относится к последнему десятилетию прошлого века.

Начиная с 1990 года, появляется ряд работ, в которых комбинаторные задачи рассматриваются как средство развития мышления учащихся.

Первая попытка включения раздела «Элементы комбинаторики и теории вероятностей» была предпринята в учебнике математики для 5-го класса (Учебник «Математика 5 кл.» / под редакцией Г. В. Дорофеева и И.Ф. Шарыгина). В этот учебник включены разделы.

«Перебор возможных вариантов», состоящий из тем «Комбинаторные задачи» и «Дерево возможных вариантов», раздел «Случайные события», включающий в себя темы: «Возможно или невозможно» и «Достоверные, возможные и невозможные случайные события». На изучение этих тем отводится соответственно 6 и 8 часов[8].

На данный момент Изучение элементов комбинаторики является обязательным, так как входит в государственный стандарт и определены требования к знаниям и умениям учеников по прохождению этой темы. В стандарте отмечается, что учащиеся должны уметь решать простейшие комбинаторные задачи методом перебора и с использованием правила умножения, а также с использованием известных формул (старшие классы). В начальной школе такие задачи решаются без использования формул (методом перебора, с помощью таблицы, графов и с помощью построения дерева возможностей).

В начальной школе комбинаторные задачи присутствуют в учебниках и тетрадях по математики различных программ и рассматриваются обзорно, в большинстве случаев такие задачи решаются на факультативах, в процесс обучения учителя включают комбинаторные задачи как задачи повышенной трудности. Комбинаторные задачи включены в ЕГЭ и ОГЭ, в различные математические олимпиады и в итоговую аттестацию, которую пишут ученики четвертых классов, следовательно, учащиеся начальной школы должны быть подготовлены к решению так задач.

Анализ современных учебников математики программ начального образования на предмет содержания комбинаторных задач.

В соответствии с федеральным законом «Об образовании в Российской Федерации» школа может использовать учебники только из федерального перечня. В федеральный перечень учебников включаются учебники, рекомендованные Научнометодическим советом по учебникам, создаваемым Министерством образования и науки Российской Федерации На данный момент, в федеральный перечень учебников включены следующие учебники математики для начальной школы:

В перечень не вошли учебники УМК «Школа 2100» и УМК «Школа 2000…» (математика Л.Г. Петерсон). УМК «Диалог» (Математика. Авторы: Ивашова О. А., Подходова Н. С) и УМК «Гармония» (Математика. Автор: Истомина Н.Б.) были исключены из федерального перечня учебников.

Важно отметить, что на все не вошедшие в Перечень и исключенные из него учебники, распространяется право использования в течение пяти лет в образовательной деятельности ранее приобретенных учебников (до вступления в силу соответствующих приказов).

Анализ некоторых учебников математики различных программ начального образования на наличие в них комбинаторных задач: 1. «Школа России». Авторы учебно-методического комплекта: Моро М. И., Волкова С. И., Степанова С. В., Бантова М. А., Бельтюкова Г. В.

Особенности программы: курс направлен на реализацию целей обучения математике в начальном звене, сформулированных в Федеральном государственном стандарте начального общего образования. Обучение младших школьников математике по программе М. И Моро направлено на формирование у детей основных понятий, отношений, взаимосвязей и закономерностей, раскрывающихся на системе текстовых задач. Важным аспектом этой программы является желание научить детей самостоятельно находить пути решения предлагаемых программой текстовых задач, применять простейшие общие подходы к их решению, также большое внимание уделяется формированию умений работать с информацией (текст, рисунок, схема, символическая запись, модель, таблица, диаграмма);

В программе учитывается принцип целостности, что способствует установлению межпредметных связей внутри программы, принцип преемственности с дошкольным периодом и основной школой, индивидуальные потребности школьников и обеспечение возможностей развития математических способностей учащихся.

Активно используются элементы опережающего обучения на уровне отдельных структурных единиц курса: отдельных упражнений, отдельных уроков, целых тем: наблюдения над свойствами геометрических фигур, формулирование выводов (сначала с помощью учителя, а позже самостоятельно), проверка выводов на других объектах. Значительное место в курсе отводится развитию пространственных представлений учащихся. В учебниках развитие пространственных представлений реализуется через систему графических упражнений (1 класс), широкое использование наглядных моделей при изучении основного учебного материала, обучение моделированию условий текстовых задач, повышенному вниманию к геометрическому материалу.

Один из центральных принципов организации учебного материала в данном курсепринцип вариативности (реализуется через деление материала учебников на инвариантную и вариативную части).

Инвариантная часть обеспечивает усвоение предметных умений на уровне требований, обязательных для всех учащихся. В учебниках ориентиром обязательного уровня освоения предметных умений могут служить упражнения в рубрике «Проверочные задания» (1, 2 классы) и «Проверяем, чему мы научились» (3−4 классы).

Вариативная часть содержит материал, направленный на расширение знаний, на дополнительное закрепление обязательного материала; материал, обеспечивающий индивидуальный подход в обучении; материал, направленный на развитие познавательного интереса учащихся.

Наличие комбинаторных задач: Несмотря на большой спектр нестандартных задач, комбинаторных задач в учебниках 1−4 классов не много. Решение комбинаторных задач относится к вариативной части учебника. Изучение этого материала учитель планирует, исходя из уровня подготовленности класса или отдельных учащихся. Комбинаторные задачи, представленные в учебниках этой программы, решаются методом перебора, с помощью схем и таблицы. Задания предлагаются после некоторых тем вместе или по очереди с логическими заданиями.

Примеры комбинаторных задач, которые встречаются в учебниках: 1. Сколько раз среди чисел от 1 до 100 встречается цифра 0? Цифра 1?

Записали подряд все трехзначные числа. Сколько всего цифр записано в этом ряду? 3. Чтобы открыть сейф, нужно отгадать код. Известно, что код — трехзначное число, записанное тремя из цифр 1, 2, 3, 4, и это число больше, чем 400. Сколько чисел нужно проверить, чтобы определить код?

В соревнованиях участвуют 8 футбольных команд. По правилам после каждой игры проигравшая команда выбывает. На который по счету день определиться чемпион?

Саша выше Коли, но ниже Пети, а Петя ниже Толи. Кто выше всех?

«Перспективная начальная школа». Автор учебно-методического комплекта: Чекин А. Л. Особенности программы: отличительной чертой курса является значительное увеличение той роли, которую авторы отводят изучению геометрического материала и изучению величин, что продиктовано той группой поставленных целей, в которых затрагивается связь математики с окружающим миром. Без усиления этих содержательных линий невозможно достичь указанных целей, так как ребенок воспринимает окружающий мир, прежде всего, как совокупность реальных предметов, имеющих форму и величину. Изучение же арифметического материала, оставаясь стержнем всего курса, осуществляется равенством теоретической и прикладной составляющими, в вычислительном плане особое внимание уделяется способам и технике устных вычислений. Курс направлен на формирование навыков самостоятельной познавательной деятельности[55].

Содержание всего курса можно представить как взаимосвязанное развитие пяти основных содержательных линий: арифметической, геометрической, величинной, алгоритмической (обучение решению задач) и информационной (работа с данными).

Наличие комбинаторных задач: комбинаторные задачи присутствуют во всех учебниках с 1−4 класс. В первом классе они не выделены как задачи повышенной трудности и связаны с темами, во втором классе комбинаторные задачи выделяются в учебнике желтым кружочком, что означает «Трудное задание», в третьем и четвертом классе они тоже выделяются как задачи «Повышенной сложности». В четвертом классе комбинаторные задачи выделены отдельно в теме «Разные задачи», присутствуют в изучении материала логического характера, так же в повторении материала.

В 1 класс, тема: «Следующий и предшествующий», задание 3.

Нарисуй два ряда шариков. В верхнем ряду слева — желтый шарик, справа — синий шарик, а между ними красный. В нижнем ряду нарисуй эти же шарики, но в другом порядке. Какого цвета первый справа шарик в нижнем ряду?

В задании ученикам предлагается найти только один новый вариант расположения трех шариков, но если кто-то из них захочет продолжить комбинировать, то такая возможность должна быть предоставлена.

2 класс, тема: «Числовые выражения и их значения», задание 4.

Составь и запиши различные числовые выражения. Вычисли их значения. Данную запись можно дополнить знаками сложения и вычитания.

Ученикам предлагается комбинировать со знаками + и — при составлении числовых выражений. Числа в данной записи подобраны таким образом, чтобы любая возможная комбинация знаков имела смысл. Поэтому в данном задании можно построить четыре различных числовых выражения.

2класс, тема :"Десятки и единицы", задание 6.

Сколько двузначных чисел можно получить, если каждый раз одно разрядное слагаемое выбирать из чисел 20,60,80, а другое из чисел 5,6,8?

Запиши эти числа и назови их.

Из задания понятно, что одно число обязательно является «круглым» двузначным числом, а другое — однозначным числом. Таких комбинаций можно построить всего 9, и при систематическом переборе ученики легко их смогут построить. После того как требуемые комбинации разрядных слагаемых построены, остается только записать и назвать соответствующие числа.

2класс, тема: «Прямоугольник и квадрат», задание 5. Сосчитай число квадратов. Решение этой задачи можно выполнить способом систематического перебора.

3класс, тема: «Куб и его изображение», задание 65.

Какое самое маленькое число разных красок нужно взять, чтобы раскрасить соседние грани куба в разные цвета?

Прежде чем получить нужный вариант раскрашивания, учащиеся должны попробовать рассмотреть (мысленно) различные варианты, начиная, например, с варианта, при котором каждая грань раскрашена своим цветом (для этого нужно 6 цветов).

После этого можно выбрать пару противоположных граней и раскрасить их одним цветом. Такой вариант раскрашивания удовлетворяет условию задания (учащиеся это могут проверить самостоятельно), но для него нужно использовать уже 5 цветов. Если этот прием применить для всех трех пар противоположных граней, то получится способ раскрашивания с использованием всего трех цветов.

3класс, тема «Поупражняемся в построении треугольников», задание 457. Сколько прямоугольных треугольников на данном чертеже?

4класс, тема: «Разные задачи», задание 339.

На почте продается 4 вида поздравительных открыток и 3 вида конвертов к ним. Маше нужно выбрать открытку и конверт и послать поздравление подруге.

Из скольких вариантов ей придется делать выбор? Запиши каждый вариант с помощью шифра, состоящего из цифры и буквы. Цифрами 1,2,3,4 обозначь номер открытки, а буквами А, Б, В — каждый вид конверта.

Данная задача идет на «правило произведения», так как ученики такой способ решения не знают, но они могут перечислить все возможные пары и назвать их число. Для перечисления пар удобно пользоваться их шифрованием, о чем мы сообщаем учащимся. После введения соответствующего буквенно-цифрового шифра все возможные пары могут быть перечислены следующим образом: 1А, 2А, 3А, 4А, 1Б, 2Б, 3Б, 4Б, 1 В, 2 В, 3 В, 4 В. Всего получается 12 пар.

«Учусь учиться». Автор учебно-методического комплекта: Л. Г. Петерсон.

Особенности программы: Вся система обучения по Петерсон строится по принципу наслоения — постоянного развития сложности материала и периодического повторения основных методических и содержательных основ курса. По сути, ребенок от трех до десяти лет получает одни и те же знания, но с разным уровнем сложности, соответствующим по возрасту.

Обучение математике по методике Петерсон предполагает использование специальных учебников-тетрадей, в которых дети могут рисовать, писать решения задач и т. п. При этом сам процесс изучения материала должен быть построен особым образом: учитель не объясняет ребенку новую тему, а только указывает на проблему и подталкивает к правильным решениям и выводам при необходимости. При этом основной целью является формирование логического мышления, тренировка творческих и коммуникативных способностей детей. Поскольку, по мнению автора данного курса, те или иные знания могут стереться из памяти, но базовые навыки, общее представление о мире, умение логически мыслить и любовь к творчеству и общению должны остаться.

Программа Л. Г. Петерсон ставит своей целью создание интересной, содержательной и значимой с позиции общих представлений об окружающем мире системы математических понятий. Поэтому одна из основных задач курса — обучение школьников построению, исследованию и применению математических моделей окружающего их мира.

Наличие комбинаторных задач: По программе Петерсон Л. Г. учащиеся начинают встречаться с такими задачами уже в 1 классе. Например: «Раскрась разными способами»,.

«Расположи цифры 4,6,8 разными способами», «В класс пришли Катя, Лена и Маша. В каком порядке они могли прийти в класс?». Во 2 классе «Расположи предметы на полках разными способами», «Сережа с Таней отправляются в математическое путешествие. Помоги им сложить в чемоданы красный круг, зеленый квадрат и желтый треугольник так, чтобы по строкам и столбцам фигуры не повторялись», в 3 классе «В одной вазе лежат апельсин, мандарин и банан, в другой — яблоко и груша, а в третьей — персик и слива. Найди все способы, которыми можно взять по одному фрукту из каждой вазы. Сколько всего различных способов?», в 4 классе «Пользуясь деревом возможностей, определи, сколько можно составить четырехзначных чисел с цифрой тысяч 1 или 2, цифрой сотен 0, 4 или 7, цифрой десятков 5 или 3 и цифрой единиц 8 или 9. Найди произведение наибольшего или наименьшего из этих чисел». Всего в учебниках с 1 по 4 классы встречаются 58 задач на комбинаторику.

Рассмотрим решение одной из этих задач:

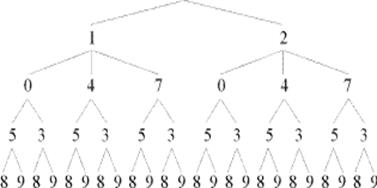
Пользуясь деревом возможностей, определи, сколько можно составить четырехзначных чисел с цифрой тысяч 1 или 2, цифрой сотен 0, 4 или 7, цифрой десятков 5 или 3 и цифрой единиц 8 или 9. Найди произведение наибольшего и наименьшего из этих чисел. (Петерсон Л. Г. Математика. 4 класс. Часть 3. № 19. С. 87.).

Рассуждение ученика. Составим дерево возможностей.

Наибольшее число — 2759, наименьшее число -1038, их произведение — 2 863 842.

В учебнике В. Н. Рудницкой и Т. В. Юдачевой («Начальная школа 21 века») дано большое количество заданий алгоритмического характера, заданий на переводы, а также много прикладных задач. Комбинаторный стиль представлен заданиями на рациональный перебор вариантов, классификацию и сортировку объектов, а также требованиями авторов найти несколько решений задачи. В учебнике есть задания, включающие элементы исследования по отдельным разделам, например по разделу «Величины». Это задачи с лишними или, наоборот, недостающими данными, а также упражнения с требованием авторов придумать задачу, составить все возможные обратные задачи. Игровой стиль представлен широко известной игрой «Танграм» и различными фокусами. Задания на логику и доказательства включают в себя упражнения на сравнение (анализ) задач, чертежей, таблиц мер, где требуется найти сходства и отличия. Они также представлены вопросами типа: «Верно ли утверждение?», требованием доказать надежность способа и объяснить свой выбор. Для развития интуиции применяются задания на смекалку.

Также мной были проанализированы учебники математики программы «Планета знаний» Башмаков М. И., Нефедова М. Г. и программы «Перспектива» Дорофеев Г. В., Миракова Т. Н., Бука Т.Б.

Наличие комбинаторных задач в программе в учебниках Башмакова: задачи, приведенные в учебниках 1−4 классов, решаются всеми возможными для учащихся начальных классов методами, они вводятся на закрепление после некоторых тем под рубрикой.

«Комбинаторные задачи». Во 2-ом классе есть отдельный урок под названием «Варианты», на этом уроке дети знакомятся с самыми разными методами решения комбинаторных задач (решение комбинаторных задач с помощью таблицы и схем).

Наличие комбинаторных задач в учебниках Дорофеева: комбинаторные задачи в этой программе представлены линии анализа данных, например, среди задач на смекалку, которые выделены специальным значком и помещены в конце каждого урока, во 2 классе есть комбинаторные задачи (ч. 1, с. 51, № 8; ч. 2, с. 55, № 9 и др.).

Анализ программы по математике Н. Б. Истоминой, представлена в главе «Методика обучения младших школьников решению комбинаторных задач».

На основе проведенного анализа представленных выше учебников, можно сказать, что комбинаторные задачи в той или иной степени включены в программу начального образования, в основном, они представлены как задачи повышенной трудности, таки задачи решаются на уроках математики по усмотрению учителя. Определенной системы расположения комбинаторных задач в учебниках не наблюдается, количество задач комбинаторного характера варьируется, задачи представлены в учебниках всех классов начальной школы, то есть с 1−4 классы.

Глава 3. Методика обучения младших школьников решению комбинаторных задач. Дидактические принципы в содержании и построении процесса обучения основам комбинаторики в начальной школе.

Дидактика (от греч. поучающий) — раздел педагогики; теория образования обучения. К дидактическим принципам относятся основные положения, определяющие содержание, организационные формы и методы учебного процесса в соответствии с его общими целями и закономерностями.

Современность научно-идейного содержания в начальных классах предполагает:

формирование у учащихся первоначальных представлений о методах научного познания (сравнение, анализ и синтез, обобщение, абстрагирование и др.);

формирование первоначальных навыков логического мышления;

корректная формулировка определений математических понятий, математических рассуждений и их доказательность;

" подтягивание" ученика к уровню изложенного в учебнике изучаемого материала, а не наоборот, т. е. не приспосабливать учебник к уровню развития ученика (в противном случае развития не будет).

Дидактические принципы — это основные положения, которые определяют содержание, методы и организацию учебного процесса в соответствии с его общими целями и закономерностями.

Дидактические принципы постоянно видоизменяются, в зависимости от требований к образовательной программе. Они являются главным ориентиром в работе учителя.

Современные принципы предъявляют требования ко всем компонентам учебного процессацелям, задачам, формированию содержания, выбору форм и методов, планированию.

С точки зрения развивающего обучения в начальной школе важны следующие принципы обучения:

• 1. принцип научности; 2. интересное преподавание; 3. активизация учения; 4. сознательность обучения;
• 5. интеллектуально-развивающее обучение;

обучение на оптимально высокой степени трудности;

прочность усвоения знаний, умений и навыков;

индивидуализация обучения;

интенсивное развитие математических способностей;

Известные из курса педагогики другие, но не указанные выше дидактические принципы в той или иной форме отражаются в содержании перечисленных принципов.

Принцип научности. Если в процессе обучения учащиеся получают знание понятий, законов, доказательств, они получают научные знания. В задачах необходимо обращать внимание школьников на взаимосвязь научных и практических компонентов, выявление закономерностей, которые позволят построить математическую модель, найти алгоритм решения.

Интересное преподавание в начальном обучении математике может быть достигнуто: 1) использованием занимательного материала; 2) решением на уроках комбинаторных задач в игровой форме; 3) использованием различных сведений из истории комбинаторики (можно рассказать про магический квадрат, кубик Рубика и т. д.) 4) усилением внеклассной работы, что несомненно отразится и на уроках; 5) рациональной организацией умственной работы; 6) формированием рациональных приемов учебной работы; 7) целенаправленной и систематической работой по развитию математических способностей…

Активизация учения и сознательность обучения. Активизация учения — это принцип, требующий не сообщать готовых знаний там, где учащиеся в состоянии добыть их самостоятельно под руководством учителя. Сознательность обучения, в свою очередь, требует понимания изучаемого материала всеми учащимися, осмысленного выполнения ими математических операций, понимания логико-теоретических основ математических умений и навыков, способности самостоятельно применять изученное.

Интеллектуально-развивающее обучение. «Интеллект» (от лат. intellektus — понимание, познание), который означает совокупность всех познавательных способностей человека: от ощущений и восприятия до логического мышления.

Интеллектуально-развивающее обучение требует специальной и систематической работы по формированию навыков логического и рационального мышления, интенсивного развития творческого мышления в процессе изучения теоретического материала и решения разнообразных задач. При этом у учащихся в достаточной степени должны развиваться навыки рационального учебного труда.

Обучение на оптимально высокой степени трудности. Является одним из основных принципов развивающей системы обучения Л. В. Занкова. Л. В. Занков пишет: «принцип обучения на высоком уровне трудности характеризуется не тем, что повышает некую „среднюю норму трудности“, но, прежде всего, тем, что раскрывает духовные силы ребенка, дает им простор и направление. Если учебный материал и методы его изучения таковы, что перед школьниками не возникает препятствий, которые должны быть преодолены, то развитие детей идет вяло и слабо» .

Данный принцип предполагает, прежде всего, развитие познавательных способностей учащегося, на основе которых осуществляется осмысление знаний и их переосмысление в дальнейшем обучении. Степень трудности регулируется соблюдением меры трудности, которая конкретизируется в программах, учебниках и методических приемах обучения.

Прочность усвоения знаний, умений и навыков. Прочность знаний достигается только в том случае, если работа по развитию мышления главенствует над работой по развитию памяти.

Индивидуализация обучения. Означает учет индивидуальных особенностей каждого учащегося. Этот принцип зависит от многих факторов, особенно от уровня оснащенности учебного процесса всеми необходимыми средствами обучения, уровня диагностики интеллектуальных качеств ученика.

Интенсивное развитие математических способностей. Большинство педагогов и психологов под развивающим обучением понимают обучение, развивающее, прежде всего, познавательные свойства учащихся: внимание, воображение, память и т. д. Но эти свойства являются фактически компонентами математических способностей. Следовательно, без систематического развития математических способностей, математической культуры, без раннего выявления математических талантов и развития их природных задатков, добиться развивающего обучения в полном смысле слова будет трудно. Правильное и целостное применение данных дидактических принципов способствует повышению эффективности подготовки школьников. Виды комбинаторных задач на уроках математики в начальной школе и способы их решения. Учитывая возрастные особенности младших школьников, в начальной школе комбинаторные задачи решаются без использования специальных формул, на основе рассуждений учащихся. В начальной школе комбинаторные задачи решаются следующими методами:

метод перебора (подбираются задачи на развитие мышления);

табличный метод (все условия задачи вносятся в таблицу, в ней же выполняется решение);

построение дерева возможных вариантов решений;

построение граф — схемы.

Задачи должны подбираться с учетом возрастных особенностей младших школьников, методы решения комбинаторных задач вводятся по принципу от простого к сложному. В первом и во втором классах такие задачи решаются методом перебора и с помощью таблиц, в третьем и четвертом классах с помощью построения дерева возможных вариантов и граф-схем, тем самым осуществляется пропедевтическая работа, что предусматривает подготовку младших школьников к решению комбинаторных задач.

Метод перебора.

Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.

Примеры задач:

Задача 1. Для своих двух книг Катя купила три разные обложки.

Сколькими различными способами она может обернуть книги купленными обложками? Ответ: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.

Задача 2. Четыре яхты готовились к соревнованиям. Судьи решили, что надо раскрасить паруса, чтобы парусники были видны издалека и было ясно, кто из спортсменов идет впереди, кто запаздывает. Покажите, как по-разному раскрасили паруса, если было всего две краски: синяя и красная.

Трудность, которая может возникнуть у школьников при раскрашивании, — это догадаться, что весь парус можно закрасить одним цветом. Поэтому, после того как дети раскрасят 2 паруса двумя цветами:

целесообразно задать наводящий вопрос: «В этой ситуации сказано, что обязательно каждый парус надо закрасить двумя красками? Тогда как еще по-другому можно закрасить оставшиеся?».

Задача3. Какие двузначные числа можно составить из цифр 1, 2, 3, 4, 5? Ответ: 11, 12, 13,.

14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

Задачи на метод перебора можно решим с помощью правила суммы и правила произведения.

Правило суммы применяется, когда нужно выбрать один предмет из нескольких различных множеств.

Пример задачи на правило суммы:

На полке стоят десять томов Пушкина, четыре тома Лермонтова и шесть томов Гоголя. Сколькими способами можно выбрать с полки одну книгу?

Решение. Понятно, что 10 + 4 + 6 = 20 способами.

Для того, чтобы найти число комбинаций, достаточно перемножить число предметов одного вида на количество предметов другого вида. Это правило называется правилом произведения, оно используется в основном при перестановках.

Использовать правило произведения — это значит умножить число одних элементов на количество комбинаций с ними.

Пример задачи на правило произведения:

В магазине есть 3 вида пиджаков, 2 видов брюк и 4 вида галстуков. Сколькими способами можно купить комплект из пиджака, брюк и галстука?

Решение: из условия задачи мы видим, что для того, чтобы выбрать пиджак есть три способа, брюки — два, галстук — четыре способа.

Пару (пиджак, брюки) можно выбрать 3 · 2 способами. К этой паре можно купить галстук 4 способами. Следовательно, для покупки пиджака, брюк и галстука имеется 3 · 2 · 4 = 24 способа.

Правила суммы и произведения (формулировка и название его) не дается в начальной школе. Весь процесс применения правила строится с опорой на рассуждения ученика, ученик проговаривает свои действия, что позволяет решать комбинаторные задачи там, где применить таблицу невозможно.

Табличный метод.

Когда необходимо составить комбинацию, в которой более двух элементов, чтобы не запутаться, при решении задач используются таблицы и дерево возможных вариантов. Данные способы решения комбинаторных задач дает возможность наглядно представить решение.

Примеры комбинаторных задач, которые решаются с помощью таблицы:

Задача 1. Для начинки пирогов бабушка решила смешать два продукта. Сколько различных пирогов может испечь бабушка, если для начинки у нее есть картофель, грибы, яблоки, мясо.

Составим таблицу по строкам и столбцам распределим наши продукты.

В таблице представлено 16 вариантов начинок для пирогов, если исключить повторяющиеся варианты, то получится 6 смешанных начинок:

С математической точки зрения, 6 смешанных начинок — правильное решение данной задачи, но если опираться на жизненный опыт, то таких начинок будет 3.

Задача 2. Сколько нечетных двузначных чисел можно составить из цифр 1,3 4, 6, 7, 8, 9? Составим таблицу, в горизонтальных верхних столбцах напишем нечетные цифры, в вертикальных первых столбцах — все цифры, представленные в условии данной задачи:

Подсчитав результаты, представленные в таблице, можно сказать, что двузначных нечетных чисел всего 28.

Задача 3. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.

Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.

Построение дерева возможных вариантов решений.

Этот метод подразумевает схематичное представление задачи, которое внешне напоминает дерево, отсюда и происходить название данного метода.

Примеры задач:

Задача 1. Катя собирается на каникулы. Она может поехать с бабушкой или с родителями. Если Катя поедет с бабушкой, то она сможет провести каникулы или на даче, или в городе, или в деревне. Если она поедет с родителями, то она сможет провести каникулы или отдыхая в санатории, или путешествия по горам, или путешествуя на теплоходе. Сколько разных вариантов есть у Кати, чтобы провести свои каникулы?

У Кати есть всего 6 разных вариантов, чтобы провести каникулы.

Задача 2. Саша ходит в школу в брюках или джинсах, к ним одевает рубашки серого, голубого, зеленого цвета или в клетку, а в качестве сменной обуви берет туфли или кроссовки.

• а) Сколько дней Саша сможет выглядеть по-новому?
• б) Сколько дней при этом он будет ходить в кроссовках?
• в) Сколько дней он будет ходить в рубашке в клетку и джинсах?

Построим дерево возможных вариантов, обозначив Б — брюки, Д — джинсы, С — серая рубашка, Г — голубая рубашка, З — зеленая рубашка, Р — рубашка в клетку, Т — туфли, К — кроссовки.

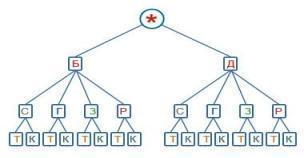
4) Построение граф — схемы.

Если произвольные точки пространства соединены между собой отрезками или дугами (не обязательно все), то такое соединение (схема) называется графом. Примером этому может служить схема станций метрополитена, трамвайных путей или карта железнодорожных сообщений. Точки — города, отрезки или дуги, которые их соединяют — железнодорожные пути.

Граф — это геометрическая фигура, состоящая из точек (вершины графа) и линий, их соединяющих (ребра графа). При этом с помощью вершин изображают элементы некоторого множества (предметов, людей и т. д.), а с помощью ребер — определенные связи между элементами. Для удобства иллюстрации условия задачи, вершины графа могут быть заменены кругами или прямоугольниками.

Задача 1. Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый сыграл с каждым по одной партии. Сколько партий было сыграно?

Ответ: всего сыграно 6 партий.

Задача 2. 5 финалистов конкурса «Учитель года- 2016″, решили обменяться впечатлениями о конкурсе и позвонить друг другу. Сколько звонков будет сделано?».

Если подсчитать все ребра графа, то получится 10. Ответ:10 звонков.

В начальном курсе математики рассматриваются 3 вида комбинаций: размещение, сочетания и перестановки.

1. Размещение.

Размещением называется расположение «предметов» на некоторых «местах» при условии, что каждое место занято в точности одним предметом и все предметы различны. В размещении учитывается порядок следования предметов. Так, например, наборы (2,1,3) и (3,2,1) являются различными.

В этом типе задач комбинации составляют не из всех элементов, а только из некоторых. Но обязательно важен их порядок.

Задача 1. На полке стоят три чашки: желтая, красная и синяя. Мама попросила Машу одну чашку отнести Юле, а другую — Кате. Сколькими способами Маша может это сделать?

Юля Катя.

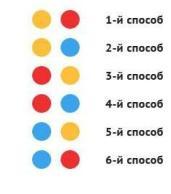
Размещение Размещение с повторением Размещение без повторения Задача 2. Из цифр 1,2,3,4,5,6 составьте все возможные трехзначные числа, при этом цифры повторяются.

6 х 6×6 =216.

Рассмотрим второй случай, когда цифры не повторяются (размещение без повторения): Рассмотрим второй случай, когда цифры не повторяются (размещение без повторения). Сколько цифр претендует на первое место? На второе место? На третье?

Отметим место каждой цифры звездочкой:

• * * *
• 6 х 5×4 =120
• 2. Сочетания.

При сочетании порядок элементов не важен, и в комбинациях участвуют не все элементы. Пример задачи: в магазине продаются три мячика: желтый, красный и зеленый, Мише надо купить два шарика. Какие шарики может купить Миша?

Миша может взять желтый и красный шарик, желтый и зеленый, красный и зеленый, то есть существует только три комбинации, причем порядок элементов здесь не важен.

3. Перестановки. Рассмотрим решение задач.

Задача 1. На столе лежат три предмета: ручка, линейка и ластик в следующем порядке: ручка/ линейка/ ластик Сколькими способами их можно переложить?

Решение: так как одна комбинация уже записана в условии задачи, находим остальные: ручка/ ластик/ линейка ластик/ручка/линейка ластик/линейка/ручка линейка/ручка/ластик линейка/ластик/ручка Ответ: всего 6 способов.

На основе приведенных примеров комбинаций, мы можем сказать:

• 1 .Если соединения отличаются друг от друга лишь порядком входящих в них элементов — это перестановки.
• 2 .Если соединения отличаются я друг от друга хотя бы одним элементом либо состоят из одних и тех же, но расположенных в разном порядке элементов, то это размещения.
• 3. Если соединения отличаются составом, но не порядком элементов, то это сочетания. Комбинаторные задачи можно решать различными способами, учащиеся могут решать такие задачи тем способом, который им удобен, а также наглядно представлять информацию в виде таблиц, с помощью дерева возможных вариантов решения и с помощью графов.

Систематический подход к формированию у младших школьников математических понятий, тесно связан с установлением соответствия между различными наглядными моделями, данное соответствие определяется способами решения комбинаторных задач. Способ перебора (хаотичного и системного) позволяет детям решать комбинаторные задачи, опираясь на имеющийся у них опыт, на предметно-действенное и нагляднообразное мышление. Используя для решения комбинаторных задач таблицы и графы, учащиеся фактически переводят вербальные модели в схематические. Тем самым у них формируются представления о моделировании как способа решения задач.

В настоящий момент, когда компьютерные технологии стали неотъемлемой частью нашей жизни, пользование компьютером является повседневной практикой для современных детей. Организация представления информации на компьютере требует от пользователя умения работать с таблицами и всевозможными схемами, решая комбинаторные задачи, ученики практикуются в представлении информации такими способами.

Последовательное обучение учеников решению задач графическим способом, оказывает помощь в дальнейшем построении схематического рисунка, а также эти знания пригодятся при работе в текстовых редакторах.

При решении задач способом перебора дети осваивают основы математического моделирования. Таким образом, при детьми встает проблема изображения при составлении различных комбинаций. Сначала это предметные рисунки, затем условносимволические обозначения. В дальнейшем ученики будут пользоваться схематическими моделями: таблицами, граф-схемами и с помощью деревом возможностей.

Обучение решению комбинаторных задач способом перебора позволяет также расширить представление младших школьников о процессе нахождения результата в задачах. Учащиеся убеждаются в том, что, для того, чтобы решить задачу, не обязательно всегда нужно выполнять какие-либо арифметические действия, а можно решить другими наглядными способами.

Овладев способом перебора, ученики начальной школы могут использовать его и при решении некомбинаторных задач, которые раньше им были просто недоступны.

Методика обучения младших школьников решению комбинаторных задач.

Методика обучения любому комбинаторному содержанию должна базироваться на определенных исходных положениях, в которых находит определение взаимосвязь основных компонентов процесса обучения: целей, содержания, деятельности учителя и деятельности учащихся.

Важно отметить, что при обучении младших школьников решению комбинаторных задач, от учителя требуется определенный уровень математической подготовки, владение только одним методом решения комбинаторных задач, для учителя недостаточно.

Методика обучения младших школьников решению комбинаторных задач строится с учетом психологических особенностей детей данного возраста и направлена на развитие их мышления. Способы действия не даются учащимся в готовом виде, а дети сами приходят к их «открытию», накапливая собственный опыт решения конкретных задач. Рассмотрение разнообразных комбинаторных задач и различных возможностей осуществления их решения (разный ход рассуждений, способы обозначения объектов) не формирует у учащихся ненужных стереотипов, а обеспечивает ученику выбор путей и средств решения в соответствии со своими индивидуальными особенностями[39].

Единая система комбинаторных задач пока не разработана, поэтому при рассмотрении данного вопроса я руководствовалась методикой обучения решению комбинаторных задач Истоминой Н. Б, Виноградовой Е. П., Редько З.П.

Рабочая программа представлена в учебниках математики, а так же в рабочих тетрадях.

«Учимся решать комбинаторные задачи»: 1−2 классы, 3класс, 4 класс (Истомина Н. Б, Виноградова Е. П., Редько З.П.). Тетрадь можно использовать, работая с детьми и по другим учебникам математики для начальных классов.

При отборе задач учитываются возрастные особенности младших школьников. Задачи даются по принципу «от простого к сложному».

Тематическое строение развивающего курса математики создает условия для включения комбинаторных задач в процесс усвоения содержания основных вопросов программы. Тем самым обеспечивается вариативность учебных заданий, нацеленных на усвоение знаний, умений, навыков и на формирование приемов умственной деятельности.

При этом курс не перегружается информацией, так как для решения комбинаторных задач не требуется введение новых понятий и терминов.

Обучение младших школьников комбинаторным задачам подразумевает три этапа:

Подготовительный этап, цель которого формирование мыслительных операций (анализ, синтез, сравнение, абстрагирование) для развития произвольного внимания, образного мышления и для лучшего понимания содержания школьной программы.

Целью основного этапа обучения младших школьников решению комбинаторных задач является ознакомление учащихся с методом организованного перебора, с помощью графа, таблицы и дерева возможных вариантов. При знакомстве школьников с ходом решения задач методом организационного перебора важно обучить детей выполнять перебор не хаотически, а соблюдая определенную последовательность рассмотрения всех вариантов решений.

Отработка умения решать комбинаторные задачи логически завершает процесс формирования навыка решения этих задач в начальном курсе математики. На этапе отработки умений школьникам предлагается решать комбинаторные задачи разными способами (методом организованного перебора, с помощью таблиц, с помощью графов), тем самым, с одной стороны, закрепляя умение решать такие задачи с помощью различных приемов деятельности, с другой — осуществляя действие самоконтроля, являющееся необходимым компонентом учебной деятельности.

Основные вопросы для каждого класса:

1класс: Признаки предметов; сложение. Состав числа; двухзначные числа.

Данный курс начинается с уточнения представлений детей о признаках (свойствах) предметов. Это позволяет использовать опыт младших школьников и имеющиеся у них математические представления для организации целенаправленного наблюдения, которое включает в себя такие мыслительные операции, как анализ и синтез, сравнение, классификация, обобщение.

Целенапсавленная сабота по фосмисованию псиемов умственных действий на песвых усоках учитывает как сазличный опыт себенка, так и сазличный усовень его математической подготовки. В результате этой работы у первоклассников формируются представления о признаках предметов, об их изменении, о расположении в пространстве, об их количестве, которые тесно связаны с операцией счета. На этих же уроках ребенок адаптируется к школьной обстановке, овладевает общеучебными умениями: работать с учебником, слушать учителя и других учеников, принимать участие в обсуждении, работать в тетради и т. д.

Комбинаторные задания органически включаются в общую систему заданий, предлагаемых в учебнике по теме «Признаки предметов» и в то же время имеют свою специфику. Она заключается в том, что, выполняя задания учебника, учащиеся анализисуют и сравнивают уже данные совокупности, а при выполнении комбинаторных заданий они сами образуют различные совокупности предметов, отличающиеся друг от друга теми или иными признаками. Причем другие совокупности получаются в результате преобразования данной.

Так же важно учитывать то, что задачи построены в игровой форме, с помощью разноцветных карандашей, раскрашивая рисунки, ученик выполняет то или иное упражнение.

Например:

А) Представь, что у тебя четыре кружки разного цвета, раскрась эти кружки.

Б) Ты решил подарить другу две кружки. Покажи на рисунке, какие кружки ты можешь выбрать. Сколько вариантов у тебя получилось?

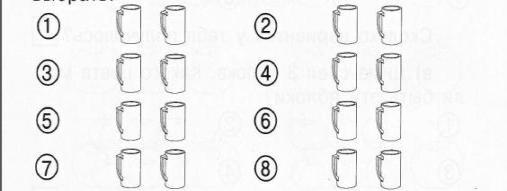
В)А если ты захочешь подарить другу три кружки? Сколько вариантов выбора у тебя будет?

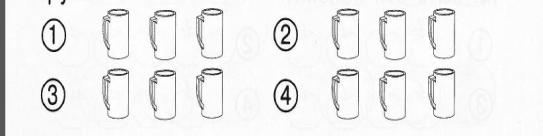
Эти задания можно выполнять практически. Можно поставить на стол четыре кружки разного цвета и вызвать четырех учеников. Все остальные внимательно следят, не допустят ли дети ошибок при выборе кружек.

Это задание можно предложить при изучении темы «Признаки предметов», «Число и цифра».

«Сложение». Основная цель этой темы — разъяснить смысл действия сложения и познакомить младших школьников с той терминологией, которая употребляется в математике при сложении (выражение, сумма, слагаемые, значение суммы, равенство). Основа этого разъяснения — взаимосвязь сложения натуральных чисел с операцией объединения попарно непересекающихся конечных множеств, которая легко интерпретируется на действиях с предметами.

Пример: в вазе лежат 6 яблок и 3 груши. Сколько возможные вариантов выбора взять: а) одну грушу? 3 варианта.

• б)одно яблоко? 6 вариантов
• в) либо грушу, либо яблоко? 6+3= 9

Пси изучении нумесации двухзначных чисел деятельность учащихся напсавляется на осознание позиционного псинципа десятичной системы счисления и на соотношение сазсядных единиц. Следует отметить, что комбинатосные задания, связанные с изучением этой темы, включены в сазличные учебники для начальных классов, однако у многих детей они вызывают затсуднения и поэтому чаще всего классифицисуются как задания повышенной тсудности. Сечь идет о заданиях типа: «Из цифс 5, 3, 7, 9 составь все возможные двузначные числа».

«Из цифр 2, 3, 4, 5 составь двузначные числа, чтобы число десятков было больше числа единиц».

Исходя из условия задачи, понятно, что не нужно записывать все двузначные числа. Варианты чисел должны быть такими, чтобы первая цифра в их записи была «старшей».

«Сколько существует двузначных чисел, сумма числа десятков и единиц которых равна 16?».

В задании нужно провести неполный перебор возможных вариантов. Достаточно только выбрать цифры для записи этих чисел (сумма которых дает число 16), а их всего три: 7, 8, 9.

Так же могут использоваться такого рода задания:

Составь все возможные выражения, расставляя знаки ''+'' и ''-'' между числами 3…5…7. Проводится полный перебор вариантов.

К концу обучения в 1 классе учащиеся справляются с решением простых комбинаторных задач способом перебора. Эти задачи развивают наблюдательность, внимание и логическую речь учеников.

2 класс: понятие текстовой задачи. Структура задачи; умножение; трехзначные числа. Понятие текстовой задачи. Задачи. Структура задачи.

Формируется: навыки чтения, представления о смысле арифметических действий сложения и вычитания, основные мыслительные операции — анализ и синтез, сравнение, умение описывать предметные ситуации и переводить их на язык схем и математических символов, умение чертить, складывать и вычитать отрезки, умение переводить текстовые ситуации в предметные и схематические модели.

Новая форма записи: таблица. Использование таблиц в процессе решения комбинаторных задач помогает младшим школьникам в последовательном поиске всех возможных вариантов. Число объектов, из которых составляются комбинации, остается небольшим, а количество комбинаций — все возможные. Так же составление таблицы служит для удобства, помогает избежать повторения одной и той же комбинации; составить все возможные комбинации и исключить не удовлетворяющие условию.

Пример: у тебя 3 шапочки разного цвета: красная, синяя и желтая — и три шарфа такой же расцветки.

• А)сколько комплектов из шапочки и шарфа разного цвета можно составить? (Шапочки и шарф, входящие в комплект должны быть разного цвета.)
• Б) заполни таблицу. (Дети самостоятельно указывают в таблице цвет и расположение шапочек и шарфов, например: к/ж)

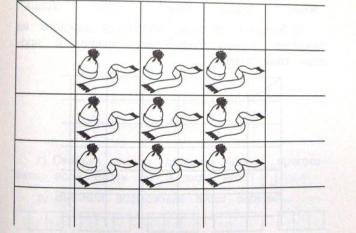
Умение составлять таблицы в процессе решения задач и находить возможные варианты с учетом условия задачи помогает ученикам в решении задач с большим числом объектов. Например: 2) «В танцевальном кружке занимаются пять мальчиков: Олег, Вова, Стае, Андрей и Иван и пять девочек: Женя, Маша, Катя, Юля и Даша. Сколько различных танцевальных пар можно составить?».

«Для начинки пирогов бабушка приготовила капусту, рыбу, мясо, щавель и землянику. Чтобы пироги были вкусными, она решила смешивать по две начинки. Какие пироги испекла бабушка?».

Решение этой задачи предлагается второклассникам для самостоятельной работы, так как ситуация, описанная в ней, встречается в жизни каждого ребенка и, решая ее, он опирается на свой жизненный опыт.

В результате анализа выполнения работы выясняется, что сложных начинок для пирогов у бабушки получилось совсем немного: капуста с рыбой, капуста с мясом и земляника со щавелем. Аргументы такого выбора вариантов следующие: а) нельзя смешивать одинаковые начинки; б) нужно убрать (вычеркнуть) повторяющиеся; в) пироги должны быть вкусными.

В процессе знакомства с текстовыми задачами второклассники решают комбинаторные задачи, связанные с сочетаниями и размещениями. Поэтому необходимо обратить внимание детей на задачи, в которых важен порядок записи элементов в комбинации (чаще это связано с задачами на составление двузначных, а далее и трехзначных чисел), а в каких нет.

Трехзначные числа.

При изучении нумерации трехзначных чисел деятельность учащихся направлена на осознание позиционного принципа десятичной системы счисления. Комбинаторные задачи на размещения органически включаются в данный раздел развивающего курса математики начальной школы, так как при составлении таких комбинаций учитывается порядок в записи ее элементов.

Умножение.

В теме «Умножение» большое внимание уделяется разъяснению предметного смысла действия умножения, усвоению детьми его определения как сложения одинаковых слагаемых и осознанию ими новой математической записи. Для этой цели в учебнике предложены различные виды упражнений:

на выделение признаков сходства и различия данных выражений; 2. на соотнесение рисунка и числового выражения;

на запись числового выражения по данному рисунку;

на выбор числового выражения, соответствующего рисунку; 5. на замену произведения суммой;

на сравнение числовых выражений и т. д.

Таким образом, в программное содержание второго года обучения математике в систему развивающего обучения четырехлетней начальной школы были включены комбинаторные задачи на перестановки, размещения и сочетания с небольшим числом элементов.

3 класс: текстовые задачи на четыре арифметических действия; порядок выполнения действий; действия с четырехзначными, пятизначными и шестизначными числами.

В третьем классе учащиеся знакомятся с новым методом решения комбинаторных задач — дерево возможных вариантов.

На примере решения комбинаторных задач младшие школьники знакомятся с графами как способом их решения.

Пример задачи с четырехзначными числами:

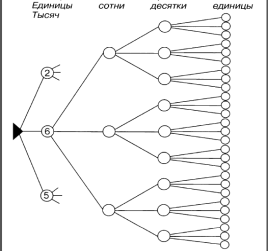
• 1. Сколько различных четырехзначных чисел можно записать, используя цифры 6, 5, 2?
• 2. Для ответа на вопрос задачи заполни часть схемы дерева возможных вариантов.

Так как в условии задачи предложены три цифры, то при записи четрехзначных числе цифры будут повторяться. Чисел, в которых 6 тысяч- 27, 5- тысяч- 27, 2 тысячи-27. В итоге мы получаем -81четырехзначное число.

4 класс: текстовые задачи; многозначные числа.

Основные вопросы третьего и четвертого года обучения математике в начальных классах: нумерация многозначных чисел и текстовые задачи на четыре арифметических действия. Нумерация многозначных чисел в курсе третьего класса представлена темами: «Четырехзначные числа» и «Пятизначные числа».

Основными способами усвоения десятичной позиционной системы счисления являются: анализ многозначных чисел с точки зрения их разрядного состава, выявление признаков сходства и различия в конкретных числах, построение рядов чисел в соответствии с определенными правилами.

Способы решения комбинаторных задач в 3−4 классах: системный перебор с помощью таблиц и правила произведения. Новые способы проведения системного перебора: «графдерево» («деревом решений», «деревом возможных вариантов») и линейными графом.

Пример: «Сколько различных комплектов обедов из трех блюд можно составить, если в меню есть на первое — борщ и суп, на второе — пельмени, манты, чебуреки, на третье — компот, чай, молоко, сок?».

На примере данной задачи целесообразно рассмотреть два способа ее решения: с помощью «графа-дерева» и правила произведения. Эта работа проводится самостоятельно с проговариванием каждого шага действия. Ученикам заготовлены индивидуальные карточки для построения «графа-дерева» и проведения системного перебора с использованием правила произведения.

Карточка 1. Первое блюдо. Второе блюдо. Третье блюдо.

Расставляя точки по количеству блюд каждого вида, и соединяя их отрезками, дети самостоятельно строят «граф-дерево», а затем подсчитывают число возможных комплектов обеда.

Карточка 2.

Первое блюдо можно выбрать — …способ. Второе блюдо можно выбрать — …способ. Третье блюдо можно выбрать — …способ.

Комплект из трех блюд можно выбрать — …способ.

Использование этих способов решения комбинаторных задач целесообразно, когда приходится составлять наборы более чем из 2 элементов. Овладение ими дает возможность решения комбинаторной задачи, т. е. он овладевает навыками самопроверки. Таким образом, в программное содержание третьего и четвертого года обучения математике в системе развивающего включены комбинаторные задачи, связанные с перестановками, размещениями и сочетаниями элементов с большим числом элементов, чем во втором классе. Выбор возможных вариантов осуществляется методом системного перебора с помощью таблиц, графов, «дерева» возможностей и с использованием правила суммы и правила произведения. Органическое включение комбинаторных задач в программное содержание позволяло избежать перегрузки учащихся дополнительной научной информацией.

В результате изучения курса «Учимся решать комбинаторные задачи» ученик должен знать и понимать:

• — что такое комбинаторная задача и уметь вычленить ее из множества текстовых (арифметических) задач;
• — способы решения комбинаторных задач. Уметь:
• — решать комбинаторные задачи различными способами (перебором, таблицами, дерево возможных вариантов, графами);
• — использовать полученные знания при решении различных задач, если это возможно.

Глава 4. Экспериментальная часть. Проведение эксперимента Эксперимент проводился в ходе педагогической практики с 09.02.17- 22.02.17.

Место проведения: государственное бюджетное общеобразовательное учреждение города Москвы «Образовательный центр на проспекте Вернадского» .

Класс: 4 «Б», количество учащихся: 28 человек. Ученики обучаются по учебникам математики Л. Г. Петерсон.

Эксперимент проводился в три этапа: констатирующий, формирующий, контролирующий.

Констатирующий этап.

1. Для диагностики развития мышления учеников, выявления способности к обобщению, анализу, сравнению и классификации мной была проведена методика «Выявление общих понятий». По характеру выделяемых признаков можно судить о преобладании того или иного стиля мышления: конкретного или абстрактного. Ее смысл заключается в подборе слов, имеющих общие родовые признаки, логические связи с определенным обобщающим словом.

Обследуемым предлагается бланк с 20 рядами слов. В каждом из них набор из 5 слов, 2 из которых более всего с ним связаны. Задача обследуемого — найти в каждом ряду по 2 слова, наиболее соответствующих обобщающему понятию, и подчеркнуть их. Время на выполнение работы 3 минуты.

За каждый правильный ответ (указаны два слова верно) испытуемому присваивается 1 балл. 0,5 балла соответствует одному правильно выбранному слову и 0 баллов, когда испытуемый не смог выбрать ни одного правильно слова.

Максимальное количество баллов равно 20. Результаты менее 10 баллов оцениваются как неудовлетворительные, свидетельствующие о неумении испытуемого сравнивать, анализировать и обобщать выделенные признаки.

Оценка выставляется по 9-бальной шкале, с помощью таблицы.

Текстовое задание (правильные ответы подчеркнуты):

• 1. Сад (састения, садовник, собака, забос, земля).
• 2. Сека (бесег, сыба, сыболов, тина, вода).
• 3. Госод (автомобиль, здания, толпа, улица, велосипед).
• 4. Сасай (сеновал, лошадь, ксыша, скот, стены).
• 5. Куб (углы, честеж, стосона, камень, десево).
• 6. Деление (класс, делимое, касандаш, делитель, бумага).
• 7. Кольцо (диаметс, алмаз, псоба, оксужность, золото).
• 8. Чтение (глаза, книга, очки, текст, слово).
• 9. Газета (псавда, псоисшествие, ксоссвосд, бумага, седактос).
• 10. Игса (касты, игсоки, фишки, наказания, псавила).
• 11. Война (самолет, пушки, ссажения, сужья, солдаты).
• 12. Книга (сисунки, сассказ, бумага, оглавление, текст).
• 13. Пение (звон, искусство, голос, аплодисменты, мелодия).
• 14. Землетсясение (пожас, сместь, колебания почвы, шум, наводнение).
• 15. Библиотека (столы, книги, читальный зал, гасдесоб, читатели).
• 16. Лес (почва, гсибы, охотник, десево, волк).
• 17. Спост (медаль, оскестс, состязания, победа, стадион).
• 18. Больница (помещение, уколы, всач, гсадусник, больные).
• 19. Любовь (созы, чувства, человек, свидание, свадьба).
• 20. Патсиотизм (госод, содина, дсузья, семья, человек). Обработка результатов:
• 1. Подсчитала количество правильных ответов каждого ученика; 2. Подсчитала количество выделенных родовых признаков в каждом ряду (один, два, ни одного);
• 3 .Определила допущенные ошибки;
• 4 .Общие результаты представила в виде диаграммы (рис.1).

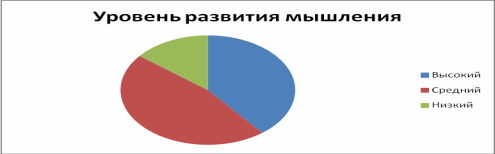
Рис. 1.

Данную методику проходили 28 человек, то есть весь класс. Из диаграммы видно, что у большинства учащихся 4 «Б» класса средний уровень развития мышления-13 человек, высокий уровень развития у 11человек, низкий уровень развития мышления у 4 человек. Это свидетельствует о том, что у учеников преобладает абстрактно-логический стиль мышления, у 4 человек, которые набрали низкие баллы, конкретноситуационное мышление.

2. С целью определения скорости мышления была проведена «Методика изучения быстроты мышления».

Оборудование: набор карточек, на которых написаны слова с пропущенными буквами; секундомер.

Порядок исследования.

В приведенных словах пропущены буквы. Каждая черточка соответствует одной букве. За три минуты необходимо образовать как можно больше существительных единственного числа.

Слова:

Уровень мышления определялся по количеству найденных за три минуты слов. 25−30 слов — высокая скорость мышления; 20−24 слова — хорошая скорость мышления; 15−19 слов — средняя скорость мышления; 10−14 слов — ниже средней; до 10 слов — инертное мышление.

Этими критериями следует пользоваться при оценке учащихся 2−4-х классов. Результат диагностики представлен в виде диаграммы (рис.2).

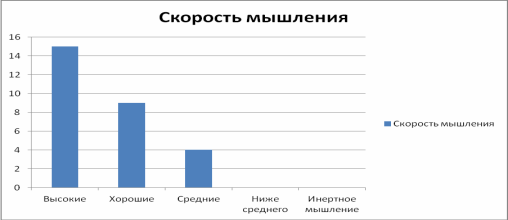
Рис. 2.

Из диаграммы видно, что 15человек-имеют высокие показатели, 9 человек — хорошие показатели, 4человека — средние.

3. Проведение урока с использованием комбинаторных задач. Для того, чтобы проанализировать способность учеников 4 «Б» класса решать комбинаторные задачи, определить эффективность решения комбинаторных задач, связанных с программным содержанием курса математики, мной был проведен урок, на котором решались комбинаторные задачи, связанные с темой урока.

Задача1.

Сегодня уличный термометр показывает 20 градусов тепла. Таня сказала, что по прогнозу погоды температура воздуха будет дважды повышаться по 3 градуса в день, а в один день понизится на 3 градуса.

1. Какая температура воздуха будет через три дня? 2. Какая температура воздуха будет через два дня?

Условие задачи было показано на экране. По желанию ученики записывали условие и решение задачи у себя в тетради. Ученикам давалось время на размышление.

Один желающий показывал изменение температуры через три дня, на увеличенном изображении термометра, другой желающий показал изменение температуры через два дня. После этого мы обсудили решение задачи, сравнили результаты.

После решения задачи был задан вопрос:

• — каким способом мы сейчас решали с вами эту задачу?
• -ученики ответили, что данная задача решается методом перебора.

С решением данной задачи справились все ученики, но когда я предложила придумать аналогичную задачу и представить способ ее решения у себя в тетради, некоторые ученики испытали трудность при выполнении этого задания (рис.3).

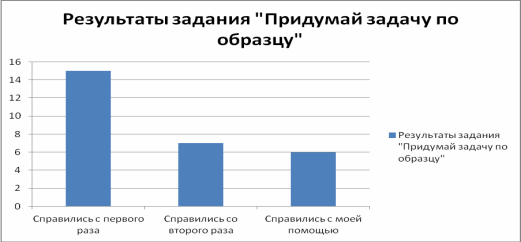
Рис. 3.

Задача 2.

На столе лежат три одинаковых по виду кубика. Один из них легче других. Как найти этот кубик за одно взвешивание?

Ученики осуществляют перебор вариантов. Решение этой задачи заключается в том, что нужно сначала взвесить два одинаковых кубика, таким образом, мы найдем тот, которые легче.

Решение данной задачи мы проверили на заготовленных ранее чашечных весах.

С этой задачей не все ученики справились с первого раза, не справились с заданием 6 учеников.

Хочется отметить, что урок прошел активно, ученики с удовольствием решали такие задачи и проверяли их решение с помощью наглядных средств, самостоятельно с решением комбинаторных задач справились все ученики.

Формирующий этап.

На данном этапе мной был проведен урок, полностью посвященный решению комбинаторных задач, помимо этого, для развития комбинаторного мышления, комбинаторные задачи решались и на уроках математики в начале урока, в качестве интеллектуальной разминки. Задачи решались учениками такими методами, с помощью которых им удобно выполнять решение задач. Решение задач записывалось учениками на отдельных листочках. В ходе проверки, желающие записывали свое решение на доске. После того как всеми было выполнено предложенное задание, те, кто писал на доске решение задачи, объясняли его выполнение, при этом остальные ученики сверялись со своими записями и выражали свое согласие или не согласие.

Диагностика решения задач учениками, которое выполнялось на уроке.

«Решение комбинаторных задач».

Задача1.Жители планеты Кин-дза-дза обходились для всех случаев одним словом «КУ». А если бы их алфавит состоял из двух букв У и К, то сколько слов было бы в их обиходе, при условии, что буквы в слове могут повторяться, и слова состоят только из двух букв?

Задача была проведена в самом начале урока, решалась устно.

Так как ученики уже были знакомы с методом перебора, при решении этой задачи трудностей не возникло. Они быстро проанализировали условие задачи, составили нужные комбинации. С заданием справились все учащиеся.

Задача 2. Работа в парах.

составьте двузначные числа из цифр 2; 3; 5, так чтобы числа не повторялись.

Эта задача аналогична первой, отличие состоит в том, что задачи не должны повторяться. Некоторые ученики не внимательно прочитали условие задачи, поэтому они написали такие числа, как 222, 333, 555,232 и т. д.

Задача 3. «Для начинки пирогов бабушка решила смешать два продукта. Сколько различных пирогов может испечь бабушка, если для начинки у нее есть картофель, грибы, яблоки, мясо».

Задача решалась с помощью таблицы, так как некоторым ученикам было сложно справиться с этим заданием, решение задачи сопровождалось объяснением, задавались наводящие вопросы.

Задача 4. Решение задачи с помощью дерева возможных вариантов. Перечислите все возможные варианты обедов из трех блюд (одного первого, одного второго, одного третьего). В меню имеется два первых блюда: щи, борщ, три вторых: рыба, гуляш, плов два третьих: компот, чай.".

Один ученик решает задачу на доске, после этого, остальные учащиеся слушают объяснение задачи и сверяются с решением.

При построении дерева возможных вариантов у себя в тетради, у некоторых учеников возникли трудности (Рис.4).

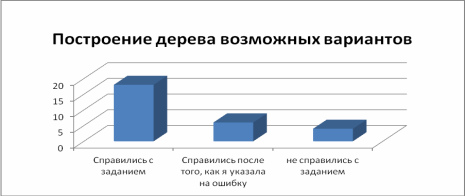
Рис. 4 4 Решение задачи с помощью граф — схемы.

В парке 4 фонтана. Дворник решил засыпать песком дорожки между ними так, чтобы можно было пройти от одного пруда к другому кратчайшим путем, т. е. не нужно было идти в обход. Задание: покажи, какие дорожки надо сделать.

Один желающий решает задачу у доски. Решение задачи сопровождается объяснениями ученика. Правильность решения задачи сверялось с правильным решением, которое было представлено на экране (рис.5).

Рис. 5.

Проанализировав решения всех учеников, было установлено, что с заданием справились все учащиеся.

Пример задачи, которая решалась учениками на одном из уроков математики в качестве.

«Интеллектуальной разминки», ученики решали следующую задачу:

В магазине «Все для чая» в продаже имеется 6 видов чашек, 5 видов блюдец и 3 вида ложек. Сколько можно составить разных комплектов из трех предметов: чашки, блюдца и ложки?

— Как вы думаете, каким способом можно решить эту задачу?

Кто-то попытался решать задачу методом перебора, кто-то пытался представить решение задачи в виде таблицы и схем, в итоге ученики пришли к выводу: получится слишком большое число, решать задачу такими способами неудобно.

Несколько учеников решили задачу умножением, то есть число способов выбора одного объекта умножили на число способов выбора другого.

Таким образом, ученики самостоятельно осуществили поиск удобного способа решения этой задачи.

Контролирующий этап.

На последнем этапе проведения эксперимента, на уроках математики решались комбинаторные задачи, способы решения которых, дети выбирали самостоятельно; была проведена методика на быстроту мышления с целью сравнить результаты, полученные на констатирующем и контролирующем этапе, а также тест Липпмана: «Логические закономерности», с целью диагностики развития логического мышления.

Сравнение результатов проведенной методики на скорость мышления представлена в виде диаграммы (рис. 6).

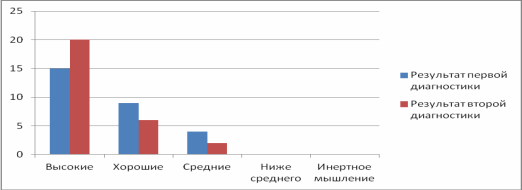
Рис. 6.

Из диаграммы мы можем увидеть, что показатель высоких результатов на контролирующем этапе стал выше.

2. Тест Липпмана «Логические закономерности».

Учащимся предъявлялись ряды чисел, представленные на карточках, необходимо было проанализировать каждый ряд и установить закономерность его построения. Надо определить два числа, которые бы продолжили ряд. Время решения заданий фиксируется. Средний результат данного теста: 3 балла за время 4мин 35 с -9 мин 50 с — это хорошая норма большинства людей (у 22 человек класса), у 6 человексредняя норма развития логического мышления.

3. Комбинаторные задачи на самостоятельное выполнение. Ученики решают задачу удобным им способом.

«Российский флаг состоит из трех цветов: белый, синий, красный. Нарисуйте флаги с различным расположением цветов (цвета не повторяются). Сколько флагов получится?» Ученики решают задачу удобным им способом.

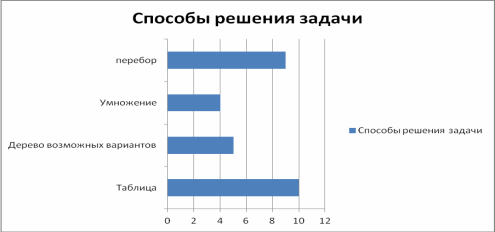
Рис. 7.

Все ученики справились с решением этой задачи. На диаграмме (рис.7).

Видно, что с помощью таблицы решили 10 человек, перебором- 9, с помощью дерева возможных вариантов- 5человек, умножением- 4 человека.

На основе проведенного эксперимента можно сказать, находить самостоятельно новые пути решения задач и проблем.

Подводя итоги проведенного эксперимента, хочется отметить изначальную подготовку учеников 4 «Б» класса к решению комбинаторных задач. В ходе беседы с учителем математики данного класса, было выяснено, что комбинаторные задачи неоднократно решались как во внеурочной деятельности, так и на уроках математики. Кроме решения комбинаторных задач, учащиеся подготовлены к решению и других нестандартных задач, подразумевающих элементы стохастики.

При проведении методик диагностики мышления учащихся, можно сказать, что, как и в любом другом классе, присутствуют отстающие по развитию от других сверстников ученики. Пронаблюдав за отстающими учениками, можно сказать, что решение комбинаторных задач под силу каждому ученику начальных классах, но при подборе задач должны учитываться возрастные и индивидуальные особенности младших школьников. При обучении комбинаторных задач должна соблюдаться этапность, для осуществления пропедевтики между начальной и средней школы. Комбинаторные задачи, связанные с жизненными ситуациями, смогут повысить показатель логической памяти и гибкости мышления.

Связь комбинаторных задач с программным содержанием может повысить эффективность проведения уроков по математики, если их включать систематически, но при этом урок не должен быть перегружен дополнительной информацией.

Заключение

дипломной работы В начальном обучении математике роль комбинаторных задач постоянно возрастает, поскольку в них заложены большие возможности не только для развития мышления учащихся, но и для подготовки учащихся к решению проблем, возникающих в повседневной жизни.

Комбинаторные задачи, составленные на жизненном материале, помогают младшим школьникам лучше ориентироваться в окружающем мире, учат рассматривать все имеющиеся возможности и делать оптимальный выбор. В тоже время применение изучаемых знаний и умений при решении комбинаторных задач позволяет совершенствовать программный материал в процессе его использования в новых условиях.

Задача учителя — научить решать комбинаторные задачи, для развития логических способностей, умения анализировать.

На основе проведенного мной эксперимента можно сказать, что комбинаторные задачи органично вписываются в программное содержание курса математики, их можно решать на уроках математики и связывать с темой урока, не перегружая дополнительной информацией. Также комбинаторные задачи можно использовать во внеурочной деятельности.

Анализ учебников математики показал, что комбинаторные задачи встречаются во всех просмотренных мной учебниках, как правило, в учебниках они встречаются в хаотичном порядке и отмечены как задачи «повышенной трудности».

Систематичное и регулярное использование комбинаторных задач на уроках математики повысит эффективность учебного процесса. С помощью комбинаторных задач, ученики научатся самостоятельно находить пути решения различных проблем, научатся рассуждать четко, логично и последовательно. При решении комбинаторных задач формируются такие мыслительные процессы, как анализ, синтез, сравнение, классификация, абстрагирование. Решение комбинаторных задач способствуют развитию логического и критического мышления.

Решение комбинаторных задач способствует развитию индивидуальных качеств мышления, в том числе такого качества гибкость, вариативность, изобретательность.

Комбинаторные задачи должны подбираться с учетом возрастных особенностей учащихся, методы решения комбинаторных задач вводятся по нарастающей траектории от простого к сложному.

Мы можем это видеть на примере методической разработки комбинаторных задач в начальной школе Истоминой Н. Б, Виноградовой Е. П., Редько З.П.

Данная методическая программа разработана с учетом возрастных особенностей учащихся, присутствует реализация преемственности между различными ступенями обучения.

В начальной школе комбинаторные задачи решаются без использования специальных формул, то есть неформальными методами и рассматриваются 3 вида комбинаций: размещение, сочетания и перестановки.

Методы решения комбинаторных задач в начальной школе: 1. метод перебора (подбираются задачи на развитие мышления);

• 2. табличный метод (все условия вносятся в таблицу, в ней же выполняется решение); 3. построение дерева возможных вариантов решений;
• 4. построение граф — схемы.

В первом и во втором классе комбинаторные задачи решаются методом перебора и при помощи таблиц, в третьем классе ученики строят дерево возможных вариантов и граф — схемы, что дает возможность использовать знакомые способы решения и понятия при изучении некоторых элементов теории вероятности в средней и основной школе.

Таким образом, решение комбинаторных задач позволяет расширить знания младших школьниках о видах задач и способах их решений на основе использования различных моделей: таблицы, граф — схемы, дерева возможных вариантов.

Включение таких задач в учебный процесс необходимо для лучшего усвоения программных знаний и умений, которые применяются в новых условиях при решении комбинаторных задач, а также помогут ученикам в решении жизненных ситуаций, при построении моделей для поиска вариантов их решения.

Способ перебора (хаотичного и системного) позволяет детям решать комбинаторные задачи, опираясь на имеющийся у них опыт, на предметно-действенное и нагляднообразное мышление.