Стохастическая интерпретация психосемантической феноменологической модели оценок социальных установок

Стохастическая интерпретация психосемантической феноменологической модели оценок социальных установок

Технология семантического дифференциала широко используется при экспериментальных исследованиях практически в любой отрасли гуманитарного направления [1−5]. Она выгодно отличается от прямого опроса, т.к. позволяет, как выявить субъективный смысл, вкладываемый респондентом в то или иное понятие, так и определить восприятие различных социальных процессов или явлений на субъективном, личностном уровне. Другими словами оценить аффективную составляющую установки опрашиваемого по отношению к заданному в анкете объекту.

Прямой же опрос выявляет когнитивный компонент установки, который гораздо меньше влияет на поведение, чем аффективный. Кроме того, ответы на прямые вопросы искажаются такими хорошо известными факторами как социальное давление, индуцирование закрытых ответов самой постановкой вопроса, разницей в восприятии вопроса самими исследователем и респондентом и т. д. [1,6].

В методе семантического дифференциала опрашиваемого просят охарактеризовать исследуемый объект по семантическим шкалам (обычно семибальным), образованным парой прилагательных-антонимов, желательно эмоциональной окраски. При этом происходит проекция субъективного, аффективного восприятия респондентом объекта в абстрактное семантическое пространство [1,2]. Но достоинства любого метода являются продолжением его недостатков. В технологии семантического дифференциала проблема интерпретации результатов гораздо сложнее, чем для прямых методов. Здесь для каждого респондента в конечном итоге получается образ исследуемого объекта в абстрактном семантическом пространстве. Причем это пространство сугубо субъективно. И весь вопрос заключается в том, как соотнести это пространство со шкалой общепринятых аффективных (эмоциональных) оценок. Нет даже гарантии, что такое соотнесение одинаково для всей совокупности респондентов.

Тем не менее, известно довольно много работ, где по полученным данным строят усредненные семантические портреты и анализируют эмоциональный отклик аудитории по величине средних первичных признаков [3]. К этому же направлению следует отнести работы, где вначале уменьшают число переменных факторным анализом, а потом строят усредненные портреты в пространстве выявленных факторов. Здесь к проблеме неодинаковости субъективных шкал еще добавляется вопрос об интерпретации полученных факторов.

Лучше дело обстоит с обработкой результатов, если при анкетировании просят оценить не один, а два или несколько объектов одной природы. Тогда, несмотря на субъективный характер семантического пространства, можно оценивать сходство или различие этих объектов. Логическим продолжением этого направления является опрос с калибровкой. Респондентов по тем же шкалам просят оценить идеально «хороший» объект и идеально «плохой» [3]. Образы идеальных конструктов задают в семантическом пространстве масштаб и направление. Теперь можно анализировать эмоциональное восприятие любого объекта того же класса по его образу в этом пространстве.

Начиная с 2009 г. и по настоящее время нами проводились регулярные исследования аффективной составляющей восприятия социальных процессов и явлений, в частности политических порядков [4,5,6−9]. При этом использовался вышеупомянутый вариант с калибровкой опроса по технологии семантического дифференциала.

Отметим, что в начале исследований, следуя общепринятому подходу, мы проводили интерпретацию по усредненному семантическому пространству [6]. Но сравнительный анализ с результатами прямого опроса, проводимого по той же анкете, показал ограниченность такого подхода, что заставило детально исследовать истоки методики обработки первичных признаков по калибровочным данным. Эта методика опирается на теорию порождения данных респондентами Кумбса, названной впоследствии теорией идеальной точки [1]. В соответствии с ней, относительное расстояние в семантическом пространстве от образа реального объекта до идеального положительного конструкта позволяет оценить предпочтение респондента, а до отрицательного — отвержение. Но свою модель Кумбс предложил именно для индивидуального уровня. И перенос на групповой, по усредненным данным, уровень, правомочен только при однородности субъективных шкал респондентов, что под большим вопросом.

В настоящий момент мы проводим анализ эмоционального восприятия исследуемых объектов на индивидуальном уровне [9]. Для количественной характеристики используется уровень восприятия, нормированный от -1 (эмоциональное отношение к идеальному отрицательному конструкту) до + 1 (восприятие идеального положительного конструкта). В соответствии с вышесказанным, его можно оценить по относительным расстояниям между соответствующими образами.

В частности, в линейном приближении уровень индивидуального эмоционального восприятия r будет пропорционален разности в семантическом пространстве относительных расстояний d_-1,x и d_+1,x. Здесь d_-1,x расстояние от образа реального объекта до точки, соответствующей отрицательному идеальному конструкту, а d_+1,x — положительному.

Отметим, что в теории Кумбса не предполагается линейная зависимость предпочтения от соответствующих близостей, а только монотонная. Более того, на основе идей, заложенных Кумбсом, впоследствии были разработаны способы определения нужной степени нелинейности в этой зависимости (см. многомерное развертывание [1]). Это статистическая методика, работающая на групповом уровне, и для индивидуальных расчетов не подходит.

Нами для решения этой проблемы был использован другой подход, основанный на концепции типичности [10,11]. В рамках теории катастроф была разработана психосемантическая феноменологическая модель, учитывающая типичные для данного класса задач нелинейности [10]. Ключевой момент модели — предположение о том, что при отклонении от стационарного состояния скорость изменения уровня восприятия описывается градиентным образом:

dr/dt=-dF/dr; (1).

где F некоторая непрерывная функция, гладким образом зависящая от вышеприведенных относительных расстояний и уровня восприятия, названная нами потенциалом восприятия. Отметим, что уравнение (1) взято нами из линейной термодинамики. Там оно описывает поведение параметра порядка при отклонении системы от равновесия и обосновано статистическим характером всех термодинамических процессов. Но в нашей задаче наблюдается аналогичная стохастичность. Человеческое восприятие и реакция всегда носят плюралистический характер, на них влияет много неучтенных факторов, и любые индивидуальные и групповые параметры имеют случайные составляющие [12,13].

Разрабатываемая модель должна быть структурно устойчива относительно таких возмущений, и от возмущений самой модели [9,10]. Откуда следует, что потенциал F должен быть общего положения (в математическом смысле [9,10]) в пространстве всех потенциалов, гладко зависящих от d_-1,x, d_+1,x и r. Здесь относительные расстояния являются внешними, управляющими параметрами, а уровень восприятия — внутренним. Как показано в теории катастроф, вид типичного потенциала определяется только от размерности внутренних и внешних параметров. В нашем случае это будет полином четвертой степени:

F=(¼)x⁴ -(½)ax² -bx; (2).

где x — параметр порядка, a и b — феноменологические параметры. Все они диффеоморфно зависят от уровня восприятия r и относительных расстояний d_-1,x и d_+1,x. В малой окрестности стационарного состояния эта зависимость переходит в линейную, конкретный вид которой был нами определен из симметрийных соображений и используемых нормировок:

a= -(d_+1x + d _-1x)/2; b= (d _-1x — d_+1x)/2; x=0,68r. (3).

Предлагаемая модель получена на основе одинаковой статистической природы термодинамических и социологических параметров. Целью настоящей работы являлось более детальное исследование этой аналогии и правомочности переноса результатов. При этом мы проводили анализ в рамках стохастического подхода, предложенного в [11] для интерпретации результатов теории катастроф.

До полной аналогии термодинамических и социологических параметров далеко. И те, и другие являются случайными величинами. Но и только. Одна из характеристик случайной величины — среднее по времени. В термодинамике используется эргодическая гипотеза, гарантирующая замену среднего по времени средним по статистическому ансамблю. Все термодинамические параметры по определению являются средними по макроскопическому ансамблю. В социологии такого понятия и эргодической гипотезы нет. В принципе, можно считать, что вся исследуемая группа является ансамблем, однако в ансамбль должны входить идентичные по свойствам составляющие. Чего конечно нет.

Случайный характер социологических переменных проявляется при многократном опросе. В этом смысле можно говорить об усреднении по времени. В предложенной модели как внешние параметры d_-1,x, d_+1,x и получаемые через них феноменологические коэффициенты, так и уровень эмоционального восприятия r являются таким средними. С другой стороны, многократного опроса респондентов, конечно, не проводилось. Получаемые при измерении индивидуальные первичные признаки (и рассчитываемее по ним относительные расстояния) являются конкретной реализацией случайных величин. Возникает вопрос, насколько правомочно их использование в модели.

Случайные величины «размазаны» по значениям и полную информацию о них дает не средние, а плотность вероятности. Для любого социологического параметра на индивидуальном уровне она может быть получена путем многократного опроса [1]. На рис. 1 для примера приведена типичная плотность вероятности, взятая из [1].

Рис. 1. Типичная плотность вероятности оценки социологического параметра a_i респондентом под номером r₁ [1]. m' - математическое ожидание.

При оценке параметра респондентом действуют много неучтенных случайных факторов. Центральная предельная теорема говорит, что в этом случае для прямых опросов функция распределения будет иметь нормальную форму. Для рассматриваемой ситуации это относится к плотности вероятности вышеупомянутых относительных расстояний и рассчитываемых через них феноменологических параметров a и b. Уровень эмоционального восприятия ищется косвенно, по нелинейным соотношениям. Нельзя гарантировать, что его распределение будет Гауссовым. Но в любом случае для устойчивого стационарного состояния плотность вероятности P подобна изображенной на Рис. 1 и математически в самой общей форме может быть представлена как [11]:

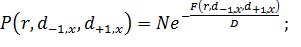
(4).

Здесь N нормировочный коэффициент, D константа, F — некая глобально минимальная функция, гладко зависящая от параметров задачи. Описание устойчивого стационарного состояния должно обладать структурной устойчивостью по отношению к имеющимся случайным возмущениям. Как мы уже обсуждали выше, отсюда следует типичность функции F. И ее конкретная реализация (2,3).

Плотность вероятности вида (4) является стационарным решением уравнения Фоккера-Планка [11]:

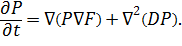
(5).

Описывающим диффузию с коэффициентом D, при наличии сноса под действие силы M=grad F. Градиенты берутся по внутреннему параметру и для нашего случая M сводится к следующему виду:

M=x³ -axbx; (6).

Из соображений непрерывности логично предположить, следуя [11], что уравнение (5) описывает не только само стационарное состояние, но и поведение уровня эмоционального восприятия (вернее его плотности вероятности) в некоторой его окрестности, при отклонении от стационарного состояния.

Уравнение Фоккера-Планка описывает плотность вероятности некоторой случайной величины. Как показано в стохастической динамике, само поведение этой величины (на уровне любой конкретной реализации) определяется соответствующим стохастическим дифференциальным уравнением [14]. Для нашего случая это будет нестрогое уравнение Ланжевена вида:

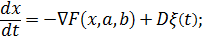
(7).

напомним, здесь параметр порядка x и феноменологические коэффициенты a, b связаны с уровнем восприятия и относительными расстояниями соотношениями (3). Последнее слагаемое о (t) обозначает быстро флуктуирующую случайную величину. Более конкретно — некоррелированный гауссов шум (белый шум). Мы указали термин «нестрогое уравнение», так как в строгом математическом смысле оно не имеет решения. А под его решением понимается любая конкретная реализация являющаяся решением интегрального стохастического уравнения [4]:

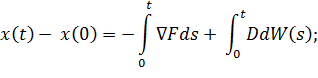
(8).

здесь первый интеграл — обычный интеграл Стильеса. Второй же — стохастический интеграл от винеровского процесса W (s), определяемого случайной величиной о (t) (dW (s) = о (t)dt). Известны две формы стохастического интеграла, Ито и Стратоновича. Для нашей задачи несущественно, какой использовать. Конечные результаты от этого не зависят.

Таким образом, уравнение Ланжевена (7) является символьной формой записи стохастического уравнении (8). Однако оно используется как для определения стохастических интегралов, так и для исследования их свойств и построения конкретных реализаций решений уравнения (8) по методу Коши-Эйлера [14]. Суть этого метода заключается в разбиении конечного интервала времени [0,t] на маленькие участки и вычислении на каждом участке по (7) приращения Дx. Здесь уже на каждом участке оДt является гауссовым случайным приращением, некоррелированным с соседними участками и разностное уравнение (7) имеет смысл. Затем устремляя шаг разбиения к нулю, получают формальное решение. А соответствующим предельным переходом определяют стохастический интеграл. Мы довольно подробно описали метод Коши-Эйлера, так как он хорошо подходит для численного моделирования и численного нахождения конкретных реализаций искомых уровней эмоционального восприятия.

В уравнениях (7) и (8) случайной величиной являться только параметр порядка x, феноменологические коэффициенты a и b детерминированы и определяются средними значениями. Кроме того, в уравнения входит коэффициент диффузии, который заранее неизвестен. Он определяет дисперсию величины x (и связанного с ним уровня восприятия r), а их то, и надо оценить в процессе интерпретации. Задача получается незамкнутой. Поэтому нами использовался немного другой подход.

В качестве уравнения Ланжевена нами использовались уравнения (1,2), но со случайными феноменологическими коэффициентами:

a=a₀ + о₁(t); b=b₀ + о₂(t); (9).

где a₀ и b₀ — средние значения случайных величин, а о₁(t) и о₂(t) — два независимых некоррелированных гауссовских шума с нулевым математическим ожиданием. Дисперсии этих шумов определяют случайные погрешности внешних параметров.

Используя метод Коши — Эйлера, для этих уравнений по каждому фиксированному разбиению всегда можно численно рассчитать приближенную реализацию случайной величины. Однако шумы в уравнение (1,2) входят не аддитивным образом, и вопрос, сходятся ли эти реализации при устремлении шага разбиения к нулю к чему либо, и описывает ли эта последовательность решение стохастического уравнения, в общем виде не исследован. В предположении малых дисперсий феноменологических коэффициентов он может быть решен положительно.

Разложим правую часть уравнения (1,2) по малым параметрам о₁(t) и о₂(t) и ограничимся линейными слагаемыми первого порядка малости. Получим уравнение Ланжевена с аддитивными шумами:

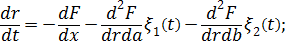
(10).

Здесь в правой части первое слагаемое и коэффициенты при шумах зависят только от средних значений, и для уравнения Ланжевена такого типа доказано существование решения, понимаемого как решение соответствующее интегрального стохастического уравнения [14].

При численном решении уравнений (1,2, 9) на каждом интервале разбиения можно провести аппроксимацию (10). Ошибка при этом будет порядка квадрата дисперсий феноменологических коэффициентов. При этом погрешности соседних участков статистически независимости и не суммируются. Таким образом, в С (1,t) норме общая погрешность не будет превышать квадрата дисперсий. И процедура Коши — Эйлера для уравнений (1,2,9) сходится в статистическом смысле (с вышеуказанной погрешностью) к некоторой случайной величине.

Главное для нас в этом результате то, что решение уравнений (1,2,9) методом Коши — Эйлера структурно устойчиво относительно величины интервала разбиения и позволяет численно рассчитывать конкретные реализации уровня эмоционального восприятия. Полные статистические характеристики этой случайной величины определялись методом Монте-Карло на агентно-ориентированном пакете имитационного моделирования Any Logic. Задавалось большое количество идентичных агентов, уровень эмоционально восприятия которых описывался уравнениями (1,2,9). Для каждого агента методом конечных разностей рассчитывалась конкретная реализация величины r с гауссовыми случайными приращениями феноменологическими параметров в соответствии с (9), независимыми как по агентам, так и по временным этапам. Плотность вероятности уровня восприятия определялась по функции распределения для всех агентов.

Отметим, что в нашей задаче присутствует два типа неопределенностей. В (9) наряду со случайной составляющей входят детерминированные средние значения феноменологических параметров. Но при измерениях мы определяли не средние, а лишь конкретные реализации первичных параметров. И по ним вычислялись конкретные реализации, как для относительных расстояний, так и феноменологических параметров по (3). Незнание средних значений внешних параметров вносит первую неопределенность, статическую. При расчетах она моделировалась тем, что параметры a₀ и b₀ для каждого агента задавались случайным образом, с гауссовским распределением. Математическое ожидание, определялось по (3) из анкетных данных, а дисперсия варьировалась для различных симуляций. Ниже, при обсуждении результатов, относительную статическую дисперсию мы обозначали как д_ст. Вторая неопределенность носит динамический характер, обусловленный случайной природой феноменологических параметров (см. (9)). Относительную динамическую дисперсию для обоих параметров мы брали одинаковой, и ниже она обозначена д_дин.

Полученные ранее экспериментальные оценки индивидуальной случайной составляющей ответов респондентов показали, что максимальная относительная погрешность не превышает 10%. Вышеотмеченные относительные расстояния в семантическом пространстве на индивидуальном уровне рассчитываются по 40 первичным признакам. Как показано еще в начале становления теории измерений в социологии, тестовый подход, заключающийся в оценке одного и того же объекта по многим параметрам и последующим сведением их к нескольким латентным факторам, сродни многократному опросу, уменьшающему случайную ошибку измерений. Поэтому в своем исследовании мы остановились на относительной дисперсии 0,05 как максимально возможной для феноменологических параметров.

Используя выше представленную методику, мы провели численные эксперименты по исследованию зависимости дисперсии результатов от случайной погрешности внешних параметров, как динамических, так и статических. Ниже показаны полученные результаты. Приводятся рассчитанные функции распределения уровня эмоционального восприятия и начальных значений феноменологических коэффициентов.

На Рис. 2, 3 показаны функции распределения первоначальных значений феноменологических коэффициентов для эксперимента с одно процентными относительными дисперсиями, как статической, так и динамической (д_ст=0,01; д_дин=0,01). По горизонтальной оси показано значение коэффициента, по вертикальной — плотность вероятности (в процентах) для этого конкретного значения. Для всех ниже приведенных функций распределений используются такие же оси координат.

Отметим, что хотя начальные значения мы задавали случайным образом с гауссовским распределением, но в каждом эксперименте наблюдалась случайная реализация этого распределения по ансамблю агентов (100 для данного эксперимента), которая значительно отличалась от классической нормальной кривой. Хотя статистические параметры распределений совпадали.

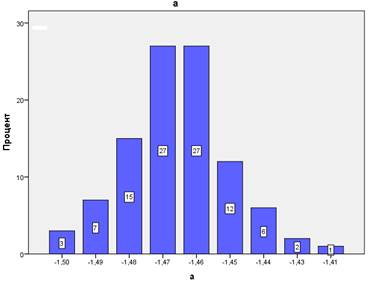
Рис. 2. Функция распределения первоначальных значений коэффициента a. Эксперимент (д_ст=0,01; д_дин=0,01).

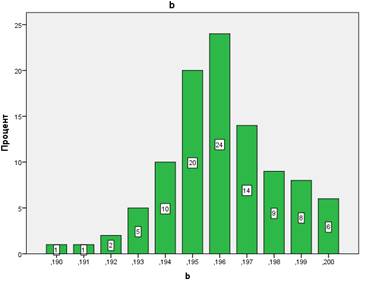
Рис. 3. Функция распределения первоначальных значений коэффициента b. Эксперимент (д_ст=0,01; д_дин=0,01).

На рисунках внутри столбиков приведены метки данных.

Результаты расчетов статистических характеристик индивидуального уровня эмоционального восприятия приведены на Рис. 4.

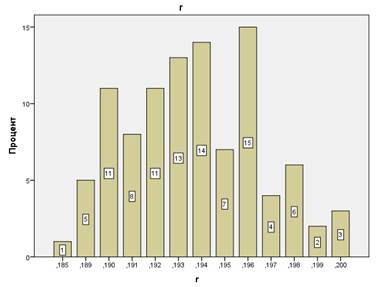
Рис. 4. Функция распределения уровня эмоционального восприятия. Эксперимент (д_ст=0,01; д_дин=0,01).

Здесь средний уровень восприятия 0,193, наиболее вероятное значение 0,196. Полученная плотность вероятности сильно отличается от гауссовой. Роль относительной дисперсии играет полуширина по уровню 0,5, равная в данном случае 1,5%. Это означает, что погрешности расчетов уровня восприятия по предложенной модели того же порядка, что и погрешности исходных данных и возможных динамических искажений, хотя и немного превышают их.

При уменьшении статической и динамической неопределенности внешних параметров размах функции распределения рассчитываемого уровня восприятия также монотонно уменьшается. И в пределе, с точностью численных расчетов, решение стохастического уравнения (1, 2, 9) переходит в детерминированное решение уравнения по ранее предложенной нами психосемантической феноменологической модели (1, 2, 3).

Увеличение флуктуаций внешних параметров приводит к монотонному росту размаха плотности вероятности рассчитываемого внутреннего параметра. На Рис. 5 для примера приведена функция распределения уровня восприятия, полученная в эксперименте ((д_ст=0,01; д_дин=0,1)).

Рис. 5. Функция распределения уровня эмоционального восприятия. Эксперимент (д_ст=0,01; д_дин=0,1).

Здесь средний уровень восприятия такой же, как и в предыдущем эксперименте 0,193, наиболее вероятное значение двух модально, 0,191 и 0,194. Размах кривой (полуширина по уровню 0,5), остался практически на том же уровне, 1,8%. Этот эксперимент демонстрирует слабую зависимость погрешности выходной (в нашей модели) величины от динамических искажений входных параметров. Десятикратное увеличение динамической относительной дисперсии феноменологических коэффициентов привело к незначительному росту полуширины кривой распределения на выходе модели.

Следующие три рисунка демонстрируют обратный в некотором роде эксперимент. Относительная динамическая дисперсия взята такая же, как и в первом случае (ддин=0,01), а статическая увеличена в пять раз (дст=0,01). Функции распределения используемых начальных значений феноменологических параметров приведены на Рис. 6 и 7.

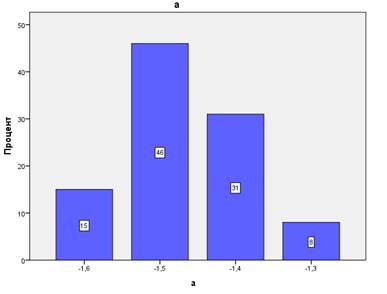
Рис. 6. Функция распределения первоначальных значений коэффициента a. Эксперимент (д_ст=0,05; д_дин=0,01).

Рис. 7. Функция распределения первоначальных значений коэффициента b. Эксперимент (д_ст=0,05; д_дин=0,01).

Плотность вероятности для рассчитываемого по модели уровня восприятия представлены на Рис. 8. Среднее его значение немного возросло до 0,194. Форма функции распределения стала ближе к нормальной. Относительный размах значительно увеличился, примерно в 4,6 раза по сравнению с первым экспериментом и стал равным 7%.

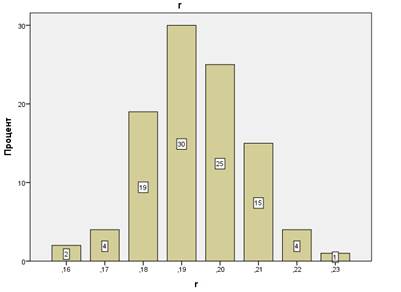
Рис. 8. Функция распределения уровня эмоционального восприятия. Эксперимент (д_ст=0,05; д_дин=0,01).

Полученный результат свидетельствует, что в разброс выходного параметра основной вклад дает статическая погрешность начальных внешних значений. Математически это понятно. Начальные значения феноменологических коэффициентов используются на каждом шаге наших расчетов. И такие погрешности на каждом этапе абсолютно коррелированны, что в первом приближении приводит к тому, что погрешность выходной величины пропорциональна статической погрешности входных параметров.

Динамические искажения учитываются в расчетах также на каждом шаге. Но шаг от шага они полностью не коррелированны, приводят к погрешностям разных знаков, что в конечном итоге уменьшает (и как мы видели значительно) размах функции распределения выходного параметра.

Следующий рисунок подтверждает эту закономерность. Увеличение динамической дисперсии в 10 раз по сравнению с предыдущим случаем практически не изменило ни размаха плотности вероятности выходного параметра (8%), ни среднего значения (0,192).

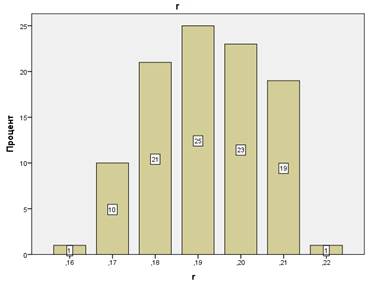
Рис. 9. Функция распределения уровня эмоционального восприятия. Эксперимент (д_ст=0,05; д_дин=0,1).

Дальнейшее увеличение статической дисперсии приводит к пропорциональному росту размазанности уровня восприятия. На Рис. 10 и 11 показаны гистограммы случайного распределения феноменологических параметров с 10% дисперсией.

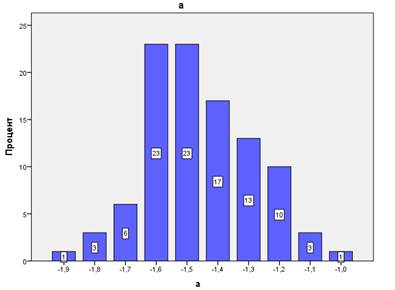
Рис. 10. Функция распределения первоначальных значений коэффициента a. Эксперимент (д_ст=0,1; д_дин=0,1).

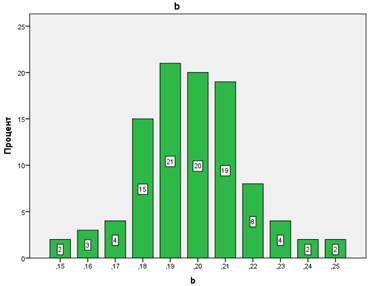
Рис. 11. Функция распределения первоначальных значений коэффициента b. Эксперимент (д_ст=0,1; д_дин=0,1).

Такие статические возмущения совместно с 10% стохастическими динамическими искажениями приводят к случайным флуктуациям рассчитываемого уровня восприятия, плотность вероятности которых приведена на Рис. 12.

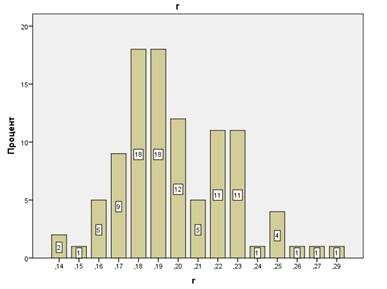
Рис. 12. Функция распределения уровня эмоционального восприятия. Эксперимент (д_ст=0,1; д_дин=0,1).

Функция распределения по внешнему виду сильно отличается от нормальной, имеет бимодальную форму. Одна мода с наиболее вероятным значением уровня в диапазоне 0,18 — 0,19. Вторая, меньшая по величине, с максимумом в диапазоне 0,22 — 0,23. Наличие второй моды привело к увеличению среднего значения до 0,2. Относительная полуширина кривой по уровню 0,5 равна 15%. Коэффициент пропорциональности между этой величиной и относительной статической дисперсией 1,5.

Отметим, что во всех проведенных нами численных экспериментах такой коэффициент был в диапазоне от 1,2 до 1,8. Для динамической дисперсии он гораздо меньше. Основное назначение предлагаемой модели — расчет индивидуальных уровней эмоционального восприятия по экспериментальным данным, полученным методом семантического дифференциала, другими словами косвенное измерение уровня восприятия. С измеренческой же точки зрения, полученные результаты означают, что в окончательную погрешность гораздо больший вклад вносят погрешности прямых измерений первичных признаков, чем динамические флуктуации восприятия респондента. При этом окончательная неопределенность задачи пропорциональна погрешности в определении входных параметров модели, что в свою очередь означает ее структурную устойчивость.

На конкретном примере мы показали действенность предложенной стохастической модели и численных методов ее реализации. Эта модель позволяет: рассчитывать индивидуальные уровни эмоционального восприятия по экспериментальным результатам, с учетом статических и динамических случайных искажений; исследовать зависимость величины погрешности расчетов от погрешностей исходных параметров; анализировать аспекты неустойчивости эмоционального восприятия; оценивать структурную устойчивость модели и полученных результатов. Конечно, структурная устойчивость, полученная для конкретных значений входных параметров (как в рассмотренном примере) еще не означает устойчивость в целом.

Однако предлагаемая модель легко обобщается и для исследования на области параметров методом Монте-Карло, реализованного в многоагентной парадигме. В рассматриваемой области задается случайное распределение точек. Каждой точке ставится в соответствие блок агентов, имеющих одинаковые средние значения входных параметров. Внутри блок разбивается на ансамбль идентичных агентов со случайным распределением первоначальных значений коэффициентов, точно также как и в вышеописанной модели. Индивидуальное поведение опять же описывается аналогичным образом. Т. е. от нашей задачи такое обобщение отличается только увеличением количества агентов.

Обобщение предложенной стохастической модели с индивидуального уровня на групповой проводится точно таким же способом. В плане интерпретации результатов опроса, каждый респондент отличается только оценками первичных признаков. В нашем случае — значением феноменологических коэффициентов. Поставим каждому респонденту в соответствие блок агентов с фиксированными коэффициентами. А внутри блока эти коэффициенты случайно распределены по идентичным агентам. При этом поведение каждого агента описывается вышеописанным способом Коши-Эйлера. Статистические характеристики всей совокупности дают как распределение респондентов по уровню эмоционального восприятия, так и оценку статической и динамической неопределенности восприятия.

В соответствии с выше полученными результатами, такая обобщенная модель в предельном случае (при устремлении индивидуальных статических и динамических флуктуаций к нулю) переходит в ранее предложенную нами психосемантическую феноменологическую модель.

• 1. Толстова Ю. Н. Измерение в социологии: Курс лекций.- М.: Инфра-М, 1998. 224 с.
• 2. Осгуд Ч., Суси Дж., Танненбаум П. Приложение методики семантического дифференциала к исследованиям по эстетике и смежным проблемам // Семиотика и искусствометрия. М.: Мир, 1972.
• 3. Архипова О. Н. Повышение эффективности сравнительных исследований с помощью качественно-количественного метода семантического дифференциала // Маркетинг в России и за рубежом. 2005. № 1. С. 76−85.
• 4. Розин М. Д., Мощенко И. Н., Джикаев Д. А. Моделирование политической напряженности методами семантического дифференциала и теории катастроф // «Математический форум. (Итоги науки. Юг России)», 2010, Т. 4, С. 341−353.
• 5. Радько К. С., Иванова М. И., Мощенко И. Н. Некоторые тренды политической напряженности среди населения Ростовской области на конец 2011 года. Инженерный вестник Дона, 2012, № 2. URL: ivdon.ru/ru/magazine/ archive/n2y2012/878.
• 6. Мягков А. Ю. Механизмы редактирования ответов респондентами (анализ зарубежных социологических теорий). Вестник ИГЭУ Вып. 1. 2008 г. URL: ispu.ru/files/str._28−32.pdf.
• 7. Мощенко И. Н. Психосемантическая феноменологическая модель групповой политической напряженности. Инженерный вестник Дона, 2010, № 1. URL: ivdon.ru/ru/magazine/archive/n1e2010/173.
• 8. Мощенко И. Н., Иванова М. И., Бугаян И. Ф. Типичные модели группового эмоционального восприятия политического порядка //Научное обозрение, 2013 г., № 2. URL: sced.ru/ru/index.php?option=com_content&view =article&id=107%3Aq &catid=21&Itemid=18.
• 9. Мощенко И. Н., А. Н. Ярошенко Эмоциональное восприятие студенчеством ДГТУ политической реальности (первая половина 2014 года). Инженерный вестник Дона, 2014, № 4. URL: ivdon.ru/ru/magazine/archive/ N4y2014/2615
• 10. Poston, T., & Stewart, I. Catastrophe theory and its applications. Courier Corporation. 2014. 472 p.
• 11. Gilmore R. Catastrophe theory for scientists and engineers. Courier Dover Publications, 1993, 666 P.
• 12. Цаллер Д. Проблема неустойчивости ответов //Социологический журнал. 2003. №. 4. С. 5 — 33.
• 13. Иванова М. И., Мощенко И. Н., Разброс оценок когнитивной составляющей группового восприятия политического порядка. Инженерный вестник Дона, 2012, № 1. URL: ivdon.ru/ru/magazine/archive/n1y2012/748.
• 14. Gardiner C.W. Handbook of stochastic methods for physics, chemistry, and the natural sciences. Berlin [etc.]: Springer. 2004. 415 p.