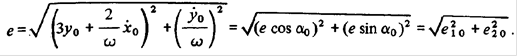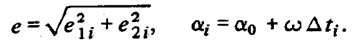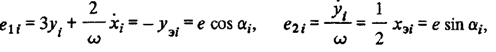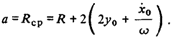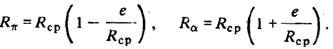Вектор эксцентриситета. 
Уравнение движения летательных аппаратов

Рассмотрим более подробно величину е, которая по компонентам вектора состояния в момент определяется формулой.

Если мы спрогнозируем вектор состояния на момент и по компонентам нового вектора состояния вновь определим е, то получим.

Существенным является то, что величина е для относительного движения, заданного начальным вектором состояния, постоянна, хотя ее компоненты меняются во времени:

т.е. можно трактовать как компоненты вектора е, модуль которого постоянен, а направление относительно осей Ох и Оу характеризуется переменным углом отсчитываемым в соответствии с рис. 2.2.

Вектор е вращается в ОСК с угловой скоростью изменения угла, т. е. со скоростью. Заметим, что относительно инерциального пространства орбитальная СК (или цилиндрическая СК) вращается также с угловой скоростью, но в направлении, обратном направлению вращения вектора е. Следовательно, можно утверждать, что направление вектора е неизменно в инерциальном пространстве и изменение его проекций в ОСК происходит только за счет вращения самой ОСК. Для того чтобы понять, как расположен вектор е относительно кеплеровой возмущенной орбиты в инерциальном пространстве, заметим, что при достигается перигей, а при возмущенной орбиты. Но при имеем, т. е. — вектор е в момент прохождения перигея направлен противоположно оси Оу (рис.5).

Как следует из рисунка, угол фактически равен фазовому углу, который пройден ЛА по возмущенной орбите от момента последнего прохождения перигея, т. е. он равен истинной аномалии ЛА.

Рис. 5 Положение вектора эксцентриситета относительно кеплеровой возмущенной орбиты.

Вектор е имеет размерность длины и в соответствии с ранее полученными результатами его компонента характеризует высотный сдвиг возмущенного движения относительно круговой орбиты, радиус которой равен большой полуоси возмущенной орбиты.

Выражения для перигейного и апогейного расстояний возмущенной орбиты могут быть теперь записаны в виде.

Из кеплеровой теории известны соотношения.

Сравнение выражений для, полученных при рассмотрении относительного движения и в кеплеровой теории, сразу определяет зависимость между эксцентриситетом относительного движения е и кеплеровым эксцентриситетом :