Алгоритмы обнаружения коллизий плоских двумерных объектов произвольной формы

Задача обнаружения и разрешения коллизий (пересечений объектов) возникает во множестве прикладных областей, таких как САПР, моделирование, физические движки, разработка тренажеров и др. [1−5].

Существующие алгоритмы разрешения столкновений не позволяют с высокой точностью и скоростью обнаружить пересечение двумерных объектов невыпуклой формы [6−8].

Целью статьи является разработка алгоритма разрешения коллизий как выпуклых, так и невыпуклых плоских объектов, отличающегося от существующих меньшими временными затратами.

Для решения данной задачи требуется постоянно измерять расстояние между двумя объектами. Если оно обращается в ноль, то тела соприкоснулись. В этом случае необходимо реализовать «скольжение» контуров без их взаимного проникновения. Поскольку контроль расстояния осуществляется с некоторым временным шагом, то вместо соприкосновения пары тел может возникнуть их взаимное проникновение. В этом случае возникает задача устранения проникновения или иной реакции на это событие.

Перечислим наиболее распространенные методы обнаружения пересечений плоских двумерных объектов.

• 1. Набор инструментов «XNA Game Studio». Все объекты описываются ограничивающими прямоугольниками, и проверяются их пересечением [6], что негативно сказывается на точности определения коллизий.
• 2. Связка алгоритмов GJK (Gilbert-Johnson-Keerthi algorithm) и EPA (Expanding Polytope Algorithm), которая использует понятие суммы Минковского [7−9]. Тела пересекаются, когда их сумма Минковского содержит начало координат, т. е. нулевой вектор.
• 3. Метод, основанный на теореме о разделяющих осях (ТРО), согласно которой пара тел не пересекается, если для них существует хотя бы одна разделяющая ось, на которой проекции тел не пересекаются [10].

На практике, теорему применяют для фигур с малым количеством граней, иначе алгоритм требует больших временных и вычислительных затрат [11].

Невыпуклые многоугольники необходимо разбить на выпуклые (рис. 1), чтобы производить обработку столкновений для каждой выпуклой части [12]. Применение выпуклой декомпозиции для методов ТРО и GJK/EPA хорошо работает только при небольших пересечениях.

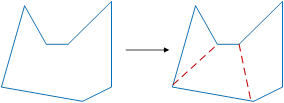
Рис. 1. — Разбиение вогнутого многоугольника на несколько выпуклых

Для разработки алгоритма обнаружения коллизий плоских двумерных объектов произвольной формы был выбран метод, основанный на теореме о разделяющих осях, так как он проще в реализации, чем алгоритм GJK/EPA и с высокой точностью позволяет разрешить столкновение объектов.

При проверке пересечений двух тел невыпуклой формы одно рассматривается как неделимый объект (без разбиения), а второе разбивается на выпуклые объекты, соответственно, поочередно проверяется пересечение первого тела с каждым выпуклым объектом второго.

Разработанный алгоритм для объектов произвольной формы состоит из следующих шагов:

1. Для каждого полигона PА и PВ строим грани по заданным координатам точек фигур:

.

.

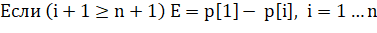
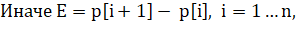
где i — номер точки, принимающий значение от 1 до n (n — количество точек полигона);

p[i] - точка фигуры с координатами x и y, для которой строим грани;

E — текущая грань.

2. Подсчитываем общее количество граней рассматриваемых объектов (, m — общее количество граней).

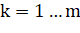
3. Берем грань с номером 1 ().

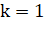
4. Строим разделяющую ось перпендикулярную к текущей грани E[k]:

.

где A — разделяющая ось для грани E[k];

Y — координата по y грани E[k], которая используется в качестве координаты x разделяющей оси, А с отрицательным знаком;

X — координата по x грани E[k], которая используется в качестве координаты y разделяющей оси А.

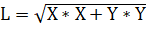
5. Нормируем длину полученной разделяющей оси А:

.

.

.

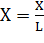
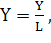
где L — длинна разделяющей оси А;

Х — координаты по х разделяющей оси А;

Y — координаты по у разделяющей оси А.

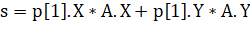
• 6. Получаем минимум и максимум проекции полигонов PА и PB на разделяющую ось А, для этого накладываем проекции фигур на данную разделяющую ось:
• 1) вычисляем скалярное произведение между первой точкой объекта и разделяющей осью А:

.

.

.

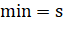
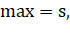
где s — скалярное произведение между текущей точкой полигона и разделяющей осью А; пересечение выпуклый декомпозиция ось.

p[1]. X, p[1]. Y — координаты по х и у текущей точки объекта;

A.X, A. Y — координаты по х и у разделяющей оси А;

min, max — минимальное и максимальное значение проекции полигона на разделяющую ось А.

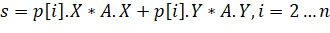
2) вычисляем скалярное произведение.

.

.

.

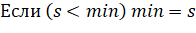
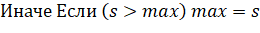
7. Вычисляем расстояние между проекциями полигонов PА и PB, с помощью переменных minA, maxA, minB, maxB:

.

.

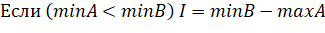
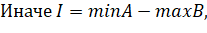
где I — дистанция между проекциями объектов, А и В.

• 8. Если расстояние I между проекциями больше нуля, значит, полигоны не пересекаютcя, переходим на шаг 16, иначе на шаг 9.
• 9. Если текущая грань принадлежит объекту PА и данный объект является невыпуклым, то вычисляем расстояние между проекциями объекта PB и текущей грани Е[k] на разделяющую ось А, иначе переходим на шаг 11:
• 1) в качестве минимума и максимума проекции грани Е[

.

.

где pА).

2).

Е[k.

.

3) переходим на шаг 11.

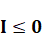
• 10. Если ни одна из граней полигона PА (объект PА является невыпуклым) не пересекается с полигоном PB, то полигоны точно не пересекаются, переходим на шаг 16, иначе на шаг 11.
• 11. Проверяем, является ли вычисленное расстояние I для текущей разделяющей оси, А минимальным по сравнению со значениями, полученными на других возможных разделяющих осях объектов PА и PB:

.

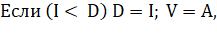
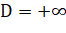
где D — минимальное расстояние между проекциями полигонов по умолчанию ;

V — вектор, равный разделяющей оси, на которой наложение проекций полигонов минимально.

• 12. Если текущая грань является последней из общего количества граней объектов PА и PB, то переходим на шаг 13, иначе переходим к следующей грани () на шаг 4.
• 13. Получаем вектор перемещения, необходимый для вывода объектов, А и В из состояния пересечения:

.

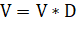
14. Определяем знак вектора перемещения:

.

.

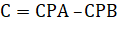
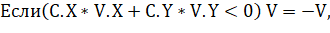
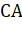
где , — координаты центров объектов PА и PB;

С — разница между центрами объектов;

С.Х, С. Y — координаты по осям х и у переменной С.

V.Х, V. Y — координаты по осям х и у вектора перемещения V.

• 15. Смещаем полигон PА на полученный вектор перемещения V для вывода объектов из состояния пересечения.
• 16. Конец.

Было проведено тестирование работы алгоритма на нескольких наборах невыпуклых объектов. На рис. 2 представлен пример разрешения коллизий двух невыпуклых объектов разработанным алгоритмом.

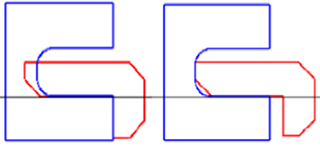
Рис. 2. — Пример разрешения коллизий двух невыпуклых объектов

Предложенный алгоритм, алгоритмы «ТРО» и GJK/EPA были протестированы на одинаковых наборах невыпуклых объектов в идентичных условиях (результаты представлены на рис. 3).

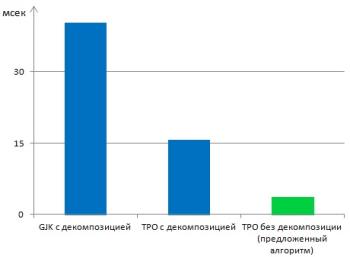
Рис. 3. — Среднее время разрешения коллизий (мсек)

Как видно из гистограммы, предложенный алгоритм работает в 4 раза быстрее алгоритма «ТРО» и 10 раз быстрее GJK/EPA с выпуклой декомпозицией.

Таким образом, в работе предложен алгоритм, отличающийся отсутствием выпуклой декомпозиции невыпуклых объектов, показана эффективность разработанного алгоритма, который работает в среднем в три — четыре раза быстрее по сравнению с алгоритмом «ТРО», использующего выпуклую декомпозицию, и в восемь — десять раз, чем алгоритм GJK/EPA.

• 1. Файзрахманов Р. А., Бакунов Р. Р., Мехоношин А. С. Создание трехмерных моделей для системы визуализации тренажерного комплекса // Вестник Пермского национального исследовательского политехнического университета. Электротехника, информационные технологии, системы управления. — 2012. — № 6. С. 25−30.
• 2. Fayzrakhmanov R.A., Murzakaev R. T., Mezentsev A. S., Shilov V. S. Applying the greedy algorithm for reducing the dimensionality of the dynamic programming method in solving the one-dimensional cutting stock problem // Middle-East Journal of Scientific Research. — 2014. — № 19 (3). — pp. 412−416.
• 3. Fayzrakhmanov R.A., Murzakaev R. T., Mezentsev A. S., Shilov V. S. Application of the Group Decoder for Solving the Orthogonal Materials Cutting Problem // World Applied Sciences Journal. — 2013. — № 28 (10). — pp. 1361−1365.
• 4. Ермолин Е. Н. Методы определения и разрешения столкновений на полигональных моделях: дис. канд. физико-математических наук: 05.13.18. Новосибирск, 2011. — 155 c.
• 5. Мурзакаев Р. Т., Швецов М. Д., Брюханова А. А. Алгоритмы распознавания столкновений // Международная научно-практическая конференция «Тенденции развития точных, естественных и гуманитарных наук — 2014» (сборник статей), Брянск, 21−23 июля 2014. — Брянск, 2014. — С. 3−8.

Аннотация В работе перечислены наиболее распространенные методы обнаружения пересечений и предложен алгоритм для разрешения коллизий плоских двумерных объектов сложной невыпуклой формы. Разработанный алгоритм отличается отсутствием выпуклой декомпозиции невыпуклых объектов. Приведены примеры разрешения коллизий двух невыпуклых объектов. Произведена оценка среднего времени разрешения коллизий. Показана эффективность разработанного алгоритма, который работает более чем в три раза быстрее рассматриваемых аналогов.

Ключевые слова: алгоритм обнаружения коллизий, плоские двумерные объекты, невыпуклые контуры, выпуклая декомпозиция, алгоритм GJK/EPA, сумма Минковского, теорема о разделяющих осях.