Использование фильтра Калмана в обработке данных хода напряженности электрического поля атмосферы

Аннотация

В статье рассмотрено применение цифровой обработки для улучшения качества данных, полученных с помощью сети датчиков измерения напряженности поля EFM550 производства фирмы «Vaisala», работающих в составе аппаратно-программного комплекса в центре мониторинга геофизической обстановки над южным регионом Российской Федерации при ФГБУ «Высокогорный геофизический институт». Исследуются возможности применения калмановской фильтрации для уточнения данных приборных измерений напряженности электрического поля атмосферы. Проводится сравнительный анализ полученных данных хода напряженности электрического поля до и после фильтрации.

Ключевые слова: электрическое поле атмосферы, измеритель напряженности электрического поля атмосферы, цифровая фильтрация, фильтр Калмана, математическая обработка данных измерений.

Одной из актуальных задач геофизического мониторинга является отслеживание вариации напряженности электрического поля атмосферы. Эта задача является неотъемлемой частью более общей проблемы физики и метеорологии — атмосферного электричества. К настоящему времени исследования напряженности электрического поля атмосферы достигли высокого уровня автоматизации и производятся массово. Данные о напряженности электрического поля Земли востребованы как в исследовательских целях, так и для решения задач раннего предупреждения о подходе грозовых очагов, в целях обеспечения требований к экологической безопасности, а так же в системах обеспечения защиты различных объектов, например, при подготовке ракетоносителей к пускам [1, 3, 5].

Для мониторинга электрофизических явлений в свободной и нарушенной атмосфере методом измерения локальной напряженности электрического поля в центре мониторинга геофизической обстановки над южным регионом Российской Федерации при ФГБУ «Высокогорный геофизический институт» создан аппаратно-программный комплекс, включающий в себя: измерители напряженности электрического поля атмосферы EFM550 фирмы Vaisala (Финляндия) [2]; программное обеспечение для решения задач измерения, передачи и визуализации значений напряженности электрического поля атмосферы. Информация в центр приема поступает на автоматическое рабочее место по каналам связи от радиолокаторов МРЛ-5, новых доплеровских станций ДМРЛ-С, грозорегистратора LS8000 и других источников [4].

Комплекс функционирует с 2010 года, были введены в эксплуатацию 4 измерителя электрического поля в атмосфере EFM550, они установлены в пунктах Нальчик, Пик Чегет, Кызбурун и Урвань. Каждый из них сопряжен с персональным компьютером, на жесткий диск которого записываются значения напряженности электрического поля атмосферы. Частота измерений значений напряженности электрического поля атмосферы составляет 2 Гц, т. е. данные фиксируются и записываются в файл каждые полсекунды. Согласно технических данных дальность репрезентативного измерения EFM550 составляет 50 км, а точность ±5% от отклонения показаний или в абсолютных значениях ± 50 В/м. Максимальные и минимальные значения напряженности, которые может измерить EFM550, находятся в диапазоне ± 10 кВ/м [1].

Сопоставление данных измерений датчиков различных моделей, встречает ряд серьезных трудностей. Это связано не только с различным темпом измерений или характеристиками сенсоров, но и с шумами, возникающими в результате внешних и внутренних воздействий на измерительный прибор, которые составляют так называемую погрешность измерений.

Для устранения шумов и другой лишней информации существуют специальные алгоритмы цифровой обработки данных называемые фильтрами [6, 7]. Необходимо отметить, что задача фильтрации — это не задача сглаживания. То есть фильтр применяется не для сглаживания данных с датчика, а чтобы получить наиболее близкое значение к реальной величине напряженности поля атмосферы.

В качестве такого фильтра авторами был выбран фильтр Калмана. Фильтр назван по имени венгерско-американского инженера-электрика Рудольфа Калмана. Этот фильтр нашел широкое применение в геофизических, инженерно-технических и эконометрических приложениях: от радаров и систем машинного зрения до оценок параметров экономических моделей, он является важной частью теории управления системами [8, 9].

Фильтр Калмана является разновидностью рекурсивного фильтра, который оценивает состояние динамической системы по серии неточных измерений. Модель системы для фильтра Калмана исходит из предположения, что реальное состояние в момент времени получается из состояния в момент времени. Для применения фильтра Калмана необходимо, чтобы процесс изменения измеряемой величины можно было описать следующим образом [10]:

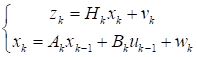
(1).

Система уравнений (1) описывает измерения отслеживаемого процесса и экстраполяцию (прогноз) его текущего состояния на основе состояния в предыдущий момент времени. Здесь — вектор измерений; — вектор состояния; матрица размерностью отображает состояние наблюдаемого процесса в измерения; — случайная величина, характеризующая погрешности измерений; — матрица размерностью, соответствующая модели преобразования системы со временем, т. е. описывающая переход наблюдаемого процесса из предыдущего состояния в состояние; является случайной величиной, описывающей ошибку модели этого преобразования; — вектор, описывающий управляющие воздействия; — матрица размерностью, учитывающая влияние вектора управляющих воздействий из предыдущего состояния в изменение состояния. Ошибка измерения и ошибка модели — случайные величины. И их законы распределения не зависят от времени (от номера итерации). Причем.

калмановская фильтрация электрическое поле.

,.

где — ковариационная матрица погрешностей измерений, а.

,.

где — ковариационная матрица погрешностей наблюдаемого процесса.

Для применения фильтра необходимо ввести следующие понятия:

• — - апостериорная оценка состояния объекта в момент, полученная по результатам наблюдений вплоть до момента включительно.
• — - апостериорная ковариационная матрица ошибок, задающая оценку точности полученной оценки вектора состояния и включающая в себя оценку дисперсий погрешности вычисленного состояния и ковариации, показывающие выявленные взаимосвязи между параметрами состояния системы.
• — - нескорректированная промежуточная апостериорная оценка состояния объекта в момент времени .
• — - нескорректированная промежуточная апостериорная ковариационная матрица ошибок.

Чтобы иметь возможность применить фильтр, необходимо определить матрицы переменных определяющих динамику системы и измерений, а значит нужно указать матрицы, и для каждого шага по времени. Матрицы и принимаются единичными матрицами не зависящими от момента времени, так как в рамках решаемой задачи считается, что измерение есть линейная комбинация вектора состояния и некоторых случайных погрешностей. Поскольку, отсутствует дополнительная информация о процессе изменения напряженности поля, поэтому полагается, что управляющее воздействие равно нулю. Ковариационная матрица погрешности измерений считается заданной. Для её задания используются данные о предполагаемой точности измерения, получаемых от датчика, эти данные указаны изготовителем. Определение параметров шума для задания ковариационной матрицы погрешностей наблюдаемого процесса — является более сложной задачей, так как требуется определить дисперсию процесса, что не всегда возможно, но можно подобрать этот параметр таким образом, чтобы он обеспечивал требуемый уровень фильтрации.

Каждая итерация фильтра Калмана состоит из двух этапов: предиктора (экстраполяции) и корректора [9, 10, 11].

На этапе предиктора вычисляется оценка по оценке вектора состояния и ковариационная матрица ошибок по следующим формулам:

.

.

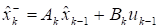
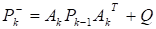
На этапе корректора вычисляется матрица коэффициентов усиления фильтра Калмана — по следующей формуле:

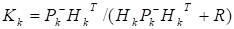
используется для коррекции оценки состояния и ковариационной матрицы ошибок следующим образом:

.

.

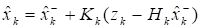
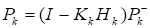
где — матрица идентичности (единичная матрица).

Для того, чтобы рекурсивный алгоритм заработал, необходимо задать начальные априорные вектор состояния и ковариационную матрицу. Поскольку они могут не совпадать с истинными значениями этих характеристик, то неверно заданные начальные условия дают искаженную оценку оцениваемого вектора состояния. Но фильтр предполагается асимптотически устойчивой системой, постепенно влияние начальных условий сойдет на нет и он станет работать устойчиво.

Так как состояние системы представлено одной переменной — напряженностью поля, то матрицы вырождаются в скалярные значения и весь алгоритм фильтра Калмана, с учетом принятых упрощений, можно изобразить в виде следующих уравнений:

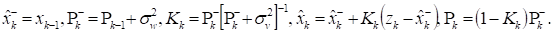
где — дисперсия ошибок модели, -дисперсия ошибок измерения, а, , известны для каждой итерации.

Пример данных полученных без фильтрации и с применением полученного алгоритма фильтра Калмана представлены на рисункe 1.

Фильтр Калмана достаточно прост в реализации, он автоматически подбирает усиление в зависимости от ошибки прогноза, причём это хорошо работает даже в присутствии шума. Благодаря пошаговой природе алгоритма, он может в реальном времени отслеживать состояние наблюдаемого процесса. Фильтр применим и в постобработке, когда есть возможность учитывать все результаты измерений, менять начальные условия, тем самым подбирая оптимальные коэффициенты.

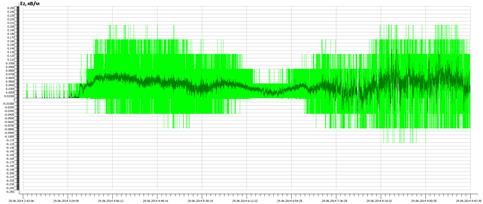
Рис. 1 — Результаты наблюдений вертикальной компоненты электрического поля атмосферы для 29 мая 2014 в пункте Кызбурун без обработки и с цифровой обработкой фильтром Калмана.

Фильтр Калмана позволяет строить более точный ход измеряемого параметра, и способствует развитию программно-математического обеспечения усвоения данных наблюдений.

По результатам проведенной работы можно сделать вывод о эффективности цифровой обработки данных напряженности нарушенного и ненарушенного электрического поля атмосферы.

• 1. Аджиев А. Х., Куповых Г. В., Кулиев Д. Д., Казакова С. Т., Малкандуева Л. М. Совместный анализ вариаций напряженности электрического поля атмосферы и грозовой активности // Известия ЮФУ. Технические науки. 2014. № 9 (158) С. 226−232.
• 2. Аджиев А. Х., Стасенко В. Н., Шаповалов А. В., Шаповалов В. А. Напряженность электрического поля атмосферы и грозовые явления на Северном Кавказе // Метеорология и гидрология. 2016. № 3. С. 46−54.
• 3. Рязанов В. И., Аджиева А. А., Шаповалов В. А. Математическое моделирование распространения примесей в атмосфере для локальной области с учетом фактических и прогнозных полей метеорологических параметров // Материалы международной научной конференции «Актуальные проблемы прикладной математики и физики». Нальчик-Терскол. 2017. С. 182.
• 4. Аджиева А. А., Шаповалов В. А. Кластерный анализ в автоматическом выявлении и сопровождении грозовых очагов по данным грозопеленгационной сети // Инженерный вестник Дона. 2016. № 2. URL: ivdon.ru/ru/magazine/archive/n2y2016/3559
• 5. Редин А. А., Новикова О. В., Куповых Г. В. Комплекс атмосферно-электрических наблюдений как элемент экологического мониторинга // Известия ЮФУ. Технические науки. 2009. № 10 С. 222−228.
• 6. Тарасова И. А., Леонова А. В., Синютин С. А. Алгоритмы фильтрации сигналов биоэлектрической природы // «Инженерный вестник Дона», 2012, № 4. URL: ivdon.ru/magazine/archive/n4p2y2012/1481
• 7. Мисюра В. В., Мисюра В. И. Обработка и распознавание сигналов. Современное состояние проблемы // Инженерный вестник Дона. 2013. № 4. URL: ivdon.ru/ru/magazine/archive/n4y2013/2130
• 8. Степанов О. А. Фильтр Калмана: история и современность // Гироскопия и навигация № 2 (69), 2010. С. 107−121.
• 9. Шахтарин Б. И. Фильтры Винера и Калмана. М.: Гелиос АРВ. 2008. 408c.
• 10. Welch G., Bishop G. An Introduction to the Kalman Filter. Department of Computer Science, UNC-Chapel Hill, TR 95−041, 2006. 16 p.
• 11. Namvaran M., Negarestani A. Noise Reduction in Radon Monitoring Data Using Kalman Filter and Application of Results in Earthquake Precursory Process Research // Act. Geophys. Volume 63, Issue 2, 2015. pp. 329−351.

References.

• 1. Adzhiev A.Kh., Kupovykh G.V., Kuliev D.D., Kazakova S.T., Malkandueva L.M. Izvestiya YuFU. Tekhnicheskie nauki. 2014. № 9 (158) pp. 226−232.
• 2. Adzhiev A.Kh., Stasenko V.N., Shapovalov A.V., Shapovalov V.A. Meteorologiya i gidrologiya. 2016. № 3. pp. 46−54.
• 3. Ryazanov V.I., Adzhieva A.A., Shapovalov V.A. Materialy mezhdunarodnoy nauchnoy konferentsii «Aktual'nye problemy prikladnoy matematiki i fiziki». Nal’chik-Terskol. 2017. p. 182.
• 4. Adzhieva A.A., Shapovalov V.A. Inћenernyj vestnik Dona (Rus), 2016. № 2. URL: ivdon.ru/ru/magazine/archive/n2y2016/3559
• 5. Redin A.A., Novikova O.V., Kupovykh G.V. Izvestiya YuFU. Tekhnicheskie nauki. 2009. № 10 pp. 222−228.
• 6. Tarasova I.A., Leonova A.V., Sinyutin S.A. Inћenernyj vestnik Dona (Rus), 2012, № 4. URL: ivdon.ru/magazine/archive/n4p2y2012/1481
• 7. Misyura V.V., Misyura V.I. Inћenernyj vestnik Dona (Rus), 2013. № 4. URL: ivdon.ru/ru/magazine/archive/n4y2013/2130
• 8. Stepanov O.A. Giroskopiya i navigatsiya № 2 (69), 2010. pp. 107−121.
• 9. Shakhtarin B.I. Fil’try Vinera i Kalmana [The filters are Wiener and Kalman]. M.: Gelios ARV. 2008. 408 p.
• 10. Welch G., Bishop G. An Introduction to the Kalman Filter. Department of Computer Science, UNC-Chapel Hill, TR 95−041, 2006. 16 p.
• 11. Namvaran M., Negarestani A. Act. Geophys. Volume 63, Issue 2, 2015. pp. 329−351.