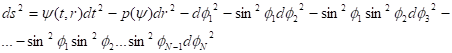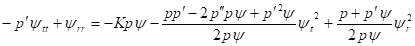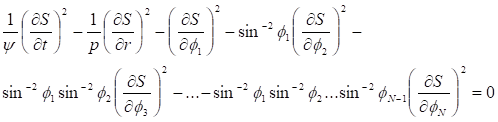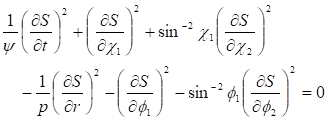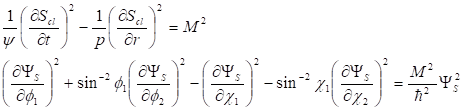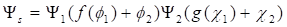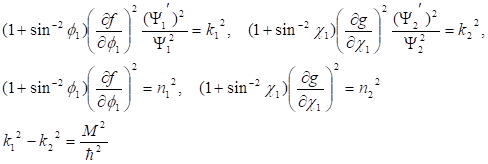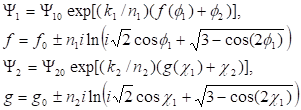Центрально-симметрические метрики. 
Единая теория поля и супергравитация в 112D

В работах [21−22] представлена модель гравитации в многомерных пространствах размерностью с метрикой.

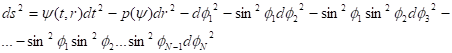
(5).

Здесь — углы на единичной сфере, погруженной в мерное пространство. Метрика (5) описывает многие важные случаи симметрии, используемые в физике элементарных частиц и в теории супергравитации. Например, 3-х сфера используется для представления симметрии; 5-сфера описывает и т. п. Такой подход позволяет охватить все многообразие материи, которую производит фабрика природы, путем выбора уравнения состояния .

Уравнения поля в метрике (5) сводятся к одному уравнению второго порядка [21−22].

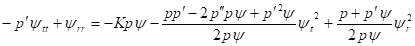
(6).

В общем случае параметры модели и скалярная кривизна зависят только от размерности пространства, имеем.

(7).

Уравнение Гамильтона-Якоби в метрике (5) имеет вид.

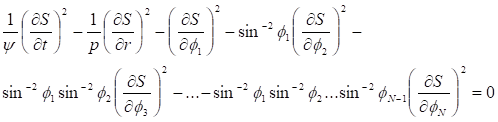
(8).

Уравнение (8) можно проинтегрировать при некоторых предположениях, используя метод, рассмотренный в работах [21−22].

В шестимерном пространстве с сигнатурой метрики можно построить естественное обобщение метрики (5) на случай наличия двух центров симметрии в виде [6].

(9).

Здесь — углы на единичных сферах, погруженных в трехмерные пространства; - координаты, связанные со временем и расстоянием соответственно.

Рассмотрим гравитацию в пространствах с метрикой (9). Заметим, что только четыре компоненты тензора Эйнштейна в метрике (9) отличны от нуля:

(10).

Следовательно, в этом случае в первом уравнении (1) следует положить, тогда уравнения поля в метрике (9) сводятся к одному уравнению второго порядка. Отсюда находим.

Уравнение Гамильтона-Якоби в метрике (11) имеет вид.

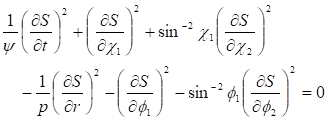
(12).

Уравнение (12) можно проинтегрировать при некоторых предположениях, используя метод, который предложил Шредингер. Суть метода состоит в том, чтобы представить решение уравнения (12) в виде.

(13).

Здесь в теорию в явном виде вводится классическое действие —, постоянная Планка и волновая функция. В случае метрики (9) удобно будет выбрать в качестве переменных квантовой механики углы на единичных сферах, а в качестве координат классического действия — время и радиальную координату. Тогда уравнение (12) разделяется на два уравнения.

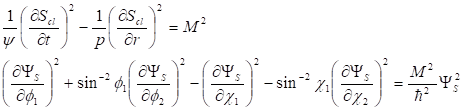
(14).

Здесь — произвольная постоянная. Рассмотрим волновые решения второго уравнения (14), зависящие от четырех переменных.

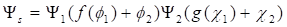
(15).

Подставляя выражение (15) во второе уравнение (14) и разделяя переменные, находим.

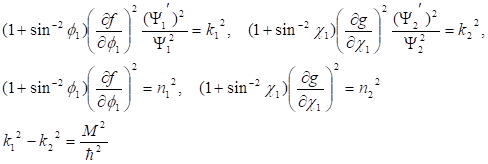
(16).

Разрешая систему уравнений (16), получим окончательно.

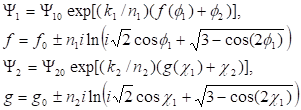
(17).

Здесь — произвольные постоянные. Функция Гамильтона-Якоби системы согласно (13) равна.

(18).

Отметим, что функция Гамильтона-Якоби является аналогом функции, описывающей волновой фронт в геометрической оптике. Периодическая зависимость функции (18) от двух переменных означает, что здесь мы имеем дело с особого рода волновым движением, охватывающим две сферы. При отображении в трехмерных мирах эти волны имеют вид раковин различной конфигурации [6].