Накопления. 
Интенсивность процентов

Выберем некоторый промежуток времени в качестве единичного (как правило, это один год) и предположим, что процентная ставка за этот промежуток равна г. Допустим, что в момент С0 = 0 сумма С инвестируется на п единиц времени. Принцип сложных процентов означает, что в момент (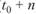) капитал С превратится в сумму.

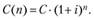(6.1).

Рассмотрим теперь вопрос о том, как справедливым образом определить доход на капитал, который инвестирован на время п/р.

Обозначим эффективную процентную ставку для промежутка 1 /р через г’б'). Поскольку на единичный отрезок можно смотреть как пар последовательных отрезков длиной 1/р каждый, применяя формулу (6.1) мы получим, что.

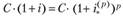
и поэтому.

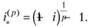(6.2).

Рассматривая отрезок 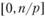как п последовательных отрезков длиной 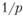каждый и применяя формулы (6.1) и (6.2), мы получим для суммы C (t), накопленной к моменту t = п/р, следующее выражение:

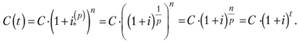
Предполагая непрерывность функции C (t), мы получим, что формула.

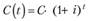(6.3).

верна для любого действительного числа .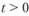

Формула (6.3) описывает процесс накопления средств в ситуации, когда принят принцип сложных процентов, и является одной из основных формул финансовой математики.

Из формулы (6.3) следует, что относительная скорость накопления средств задается формулой.

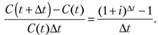
Соответственно, мгновенная относительная скорость накопления есть (согласно следствию из 2-го замечательного предела):

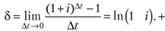(6.4).

Величина 5 в финансовой математике называется интенсивностью процентов (force of interest).

Поскольку.

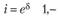(6.5).

формулу (6.3) для накоплений за время t можно переписать в виде:

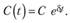(6.6).

В общем случае, когда условие 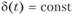не выполняется, интенсивность процентов и накопления капитала связаны между собой соотношениями:

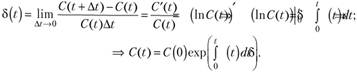
Таким образом, накопление суммы С, которую надо будет выплатить через время t составит:

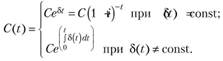
Обозначим через 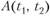отношение величины вклада в момент t2 к величине вклада в момент ?,• Эту величину называют коэффициентом накопления за промежуток времени .

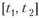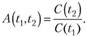
Поскольку (по определению) 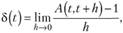верно равенство.

ПРИМЕР 6.1^[1]

Банк начисляет проценты по вкладам, используя коэффициенты накопления, основанные на переменной интенсивности процентов. 1 июля 1983 г. клиент положил? 50 000 в банк. На 1 июля 1985 г. его вклад вырос до? 59 102. Предполагая, что интенсивность процентов являлась линейной функцией времени в течение всего периода с 1 июля 1983 г. по 1 июля 1985 г., найдите интенсивность процентов 1 июля 1984 г.

Решение

Примем 1 июля 1983 г. в качестве начального момента времени, а один год — в качестве единицы измерения времени. Тогда 1 июля 1985 г. — это момент t = 2, а 1 июля 1984 г. — момент t = 1.

Поскольку (по условию) ?(?) — линейная функция от t, она дается формулой.

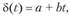
где а и h — некоторые параметры.

Тогда для коэффициента накопления за промежуток (0, t) имеем:

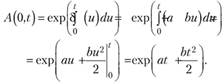
Известно, что /1(0, 2) = 59 102/50 000 = 1,18 204.

С другой стороны, из полученной выше формулы для /1(0, t) следует, что .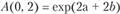

Нас интересует 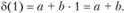Сумма фигурирует в вышеприведенной формуле для /1(0, 2), откуда ее легко найти:

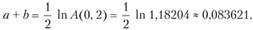
Значит, интенсивность процентов на 1 июля 1984 г. была равна 8(1) = 0,83 621.

• [1] McCutcheon J.J., Scott W. F. An Introduction to the Mathematics of Finance. Buttenvorth-Heinemann, 1986.