Принципы принятия решений для риск-менеджмента проверкой статистических гипотез

Среди задач, решаемых методом проверки статистических гипотез, наибольший интерес в риск-менеджменте представляет сравнение математических ожиданий т_х и дисперсий D_x = <�з_х числа X отказов или происшествий, характеризующих безопасность функционирования разных ОПО либо одного и того же подобного объекта, но в различные моменты времени. Потребность в этом возникает, например, при необходимости:

• а) повысить достоверность оценки соответствующего риска за счет увеличения объема выборочных данных (х, х₂,…, х_п1) путем их объединения с результатами {y_vy₂, …, у_п2) другого наблюдения;
• б) убедиться в эффективности уже реализованных мероприятий, направленных на снижение какого-либо параметра риска отказа или риска происшествия.

Проиллюстрируем возможность принятия рациональных решений в подобных ситуациях, основываясь на приведенных выше сведениях. Сделаем это на примере двух задач риск-менеджмента, использующих следующую общую информацию: 1) в качестве нулевой гипотезы Н₀ — предположение о равенстве между собой двух сравниваемых математических ожиданий: Д = т_х1— т_х2 = 0, а альтернативной Н_А гипотезы — Д Ф 0; 2) погрешность рационального выбора определяется лишь вероятностью отклонения нулевой гипотезы (ошибкой первого рода а, равной 0,05); 3) оба решения основываются на данных, допустим, о числе отказов ответственных элементов ОТУ и касаются того, как истолковывать расхождение в оценках какого-либо их параметра, рассчитанных по двум разным выборкам. А вот отличием каждого примера служит разный объем исходных данных и их происхождение.

Пример 1.

Первая задача касается рационального решения по выборочным данным большого объема. Если точнее, то требуется сравнить ущерб, вызванный отказами тех элементов ОТУ, которые были зарегистрированы на двух сходных ОПО в последние 3 года. При этом считается, что данный ущерб вызван приостановкой функционирования этих объектов, а длительность простоя зависела от эффективности системы их (массового) технического обслуживания и ремонта. Предположим также, что результаты обработки информации, полученной на данных объектах по формулам (2.4), приведены в табл. 2.3.

Таблица 2.3. Исходные данные для иллюстративного примера 1.

Для решения данного иллюстративного примера целесообразно использовать пятишаговый алгоритм проверки статистических гипотез. Однако учитывая, что его первые два шага (уточнение содержания гипотез Н₀, Н_А и выбор ошибки а) уже реализованы, ниже приведем сведения по выполнению лишь оставшихся трех (3—5) этапов основанной на нем процедуры принятия рационального решения.

3. Большой объем выборки (л > 30) дает основание принять допущение о равенстве двух выборочных оценок стандартного отклонения их действительным значениям (Oj = о_х1 иа₂ = а^), что позволяет использовать следующую нормально распределенную статистику:

• 4. Критическое значение z_a этой статистики, измеряемое долей стандартного отклонения случайной суммы (п_} + п₂) зарегистрированных отказов — знаменателя последней формулы, было определено с помощью таблицы стандартной нормально распределенной случайной величины и оказалось равным 1,645 (для, а = 0,05).
• 5. Что касается верхнего доверительного предела для статистики (2.6), то он будет равен

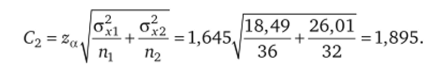
Таким образом, превышение величиной С₂ разницы между сравниваемыми оценками математических ожиданий (х₁ — х₂ = 16,1 — 14,3 = 1,8) указывает, что тяжесть последствий отказов ответственных элементов ОТУ, а значит, и обусловленный этим техногенный риск на исследуемых ОПО можно считать одинаковыми. Иначе говоря, если судить по зарегистрированным результатам и полученным на их основе оценкам, то их малозначимое отличие (возможная ошибка не превышает 5%) можно объяснить лишь случайными факторами.

Пример 2.

Вторая задача риск-менеджмента связана уже с принятием решения по малым объемам выборочных данных, полученных на одном и том же ОПО до и после модернизации его технологического оборудования (доработки конструкции ответственных элементов ОТУ). Предположим также, что искомое рациональное решение связано с оценкой эффекта от данного мероприятия на основе сведений по отказам и результатам их обработки, приведенным в табл. 2.4.

Таблица 2.4. Исходные данные иллюстративного примера 2.

Сопоставление приведенных здесь данных указывает на заметное снижение времени простоев ОПО вследствие необходимости устранения одного отказа их ОТУ. Однако для того чтобы разобраться с тем, насколько это закономерно или случайно, проведем проверку приведенных выше гипотез тем же способом, который реализован в предыдущем примере.

3. Так как малый объем выборки (п < 30) лишает основания считать выборочные оценки &J, а₂ действительными значениями стандартных отклонений а_г1 и то вместо предыдущей статистики (2.6) здесь должно использоваться уже следующее выражение:

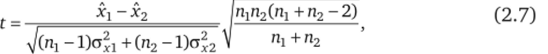
представляющее случайную величину, подчиненную распределению Стьюдента.

• 4. Критическое значение t_a выбранной статистики, опять же измеряемое долями стандартного отклонения случайной суммы (п₁ + п₂) зарегистрированных отказов, определяется уже с помощью соответствующего распределения (см. таблицу Г. 5 из приложения к этой книге). При этом для п₁ ⁺ и₂=30 и а=0,05 оказывается, что данная величина равна 1,701.
• 5. Согласно [14] нижний доверительный предел этой статистики равен

Так как значение этой величины по модулю заметно меньше разницы между сравниваемыми оценками математических ожиданий: х_г — х₂ = = 14,3 — 18,1 = -3,8, то логичен следующий вывод: тяжесть последствий отказов модернизированного технологического оборудования на исследуемом ОПО действительно снизилась, т. е. соответствующее мероприятие дало положительный эффект.

В завершение демонстрации принятия рациональных решений о равенстве двух числовых характеристик сделаем ряд дополнительных замечаний, касающихся перспективности для риск-менеджмента рассматриваемого здесь метода проверки статистических гипотез.

• 1. Прежде всего подчеркнем чрезвычайно широкие возможности обоснования рациональных решений подобным способом. Ведь принятие статистических гипотез может расцениваться как акт познания, а их априорные вероятности — как предубеждения или мера доверия к существующим исходным идеям, моделям и суждениям, что чрезвычайно важно.
• 2. Более того, открывается возможность заметного повышения достоверности принимаемых решений по мере накопления первичной информации и повышения числа п испытаний, характеризуемых одними и теми же ошибками первого (а) и второго (р) рода.

Дело в том, что после многократной обработки имеющихся сведений ошибки а (п) и (3(п) окончательного решения определяются уже следующими выражениями:

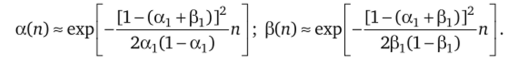
3. Данный метод применим также для проверки гипотез относительно одного среднего значения, что эквивалентно, например, интервальному оцениванию математического ожидания количества отказов или техногенных происшествий. Однако в этом случае уже применяются более простые выражения для статистик и двусторонних доверительных интервалов:

_ о* «о_х.

вместо (2.6)z =, , а для пределов С_г= т_х-z_v. C₂=m_x+z_y.

а_х/п V п '1 п.

* х-т_х _ о б вместо (2.7) t =—-р-, а для пределов Q = m_x-t"—j=, C₂ = m_x + t.—j=,

О / sin ' sin sjn

где Cj, С₂ — соответственно нижняя и верхняя границы доверительного интервала, накрывающего с вероятностью у значения оцениваемого математического ожидания.