Расчет граничных точек в пространственных методах характеристик

Пусть требуется найти численное решение уравнений (1.1) в области, ограниченной на одном из участков неизвестной границей. В процессесчета надо выстраивать эту поверхность, а также найти вдоль нее газодинамические функции 0, т, р, S, удовлетворяющие некоторым дополнительным связям (граничным условиям). 1. Рассмотрим элементарную площадку ВОСН выстраиваемой поверхности, являющуюся одной из граней расчетной ячейки в разностной схеме (рис. 2.4). Пусть в точках В, О, С известны параметры поверхности —}}).

Для достижения второго порядка аппроксимации можно привлечь ближайшие к Я точки новой плоскости согласно (24), но при этом схема становится неявной и имеет мало общего с методом характеристик.

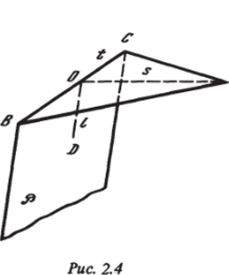
радиус-вектор г, касательные векторы г* и х в направлении ОН и ВС соответственно. Предположим также, что искомая поверхность имеет непрерывную и кусочно-гладкую нормаль п. Докажем, что для нахождения радиус-вектора г# и орта нормали п_н в расчетной точке Н искомой поверхности достаточно привлечь одну комбинацию из газодинамических уравнений (1.1), например характеристическое соотношение вдоль определенной волновой бихарактеристики (1.8). Доказательство основано на том, что г# и пн определяются с точностью до одной скалярной величины.

Действительно, из дифференциальной геометрии известно, что при выполнении соответствующих условий непрерывности и гладкости имеет место п* = ax_s + bx_tl или в разностной форме.

^гД^е (f)'s ^и (f)'t — производные в направлениях соответственно ОН и ВС, индексом 0 отмечены величины в точке О, а н b — искомые скаляры. Используя соотношение (i>, п)', *= 0, получим условие, связывающее а и Ь:

В этом соотношении t'_s, х и п в точке О известны, а правую часть можно вычислить через разностное соотношение по данным в точках В и С с учетом равенства x_ts — xⁿ_st.

Радиус-вектор точки Н определяется формулой.

Таким образом, задание радиус-вектора и нормалей в точках В_у С и О определяет близкую точку Н искомой поверхности (3) и орт нормали в ней (1), кроме одной скалярной величины, например, кроме коэффициента а в уравнении (2). Для нахождения этой величины и должно привлекаться газодинамическое условие, т. е. некоторая комбинация уравнений (1.1).

При доказательстве использована непрерывность внутри области HBOC геометрических параметров вплоть до первых производных от нормали.

Это ограничение не является обременительным при численном счете, так как непрерывность может нарушаться лишь вдоль конечного числа линий на поверхности (например, линий влияния изломов и разрывов кривизны тела на ударную волну) и расчетную схему можно выбрать таким образом, чтобы линии возможных разрывов производных проходили вдоль ВОС или через точку Н.

Соотношения (1) — (3) являются очевидными геометрическими свойствами поверхности и в любой схеме пространственного метода характеристик (точнее, в любом численном методе) при расчете произвольной граничной поверхности либо должны быть использованы непосредственно, либо их выполнение должно быть обеспечено.

Далее всюду будем рассматривать уравнение искомой поверхности г = R (z, ф) в цилиндрической системе координат z, г, и ее единичную нормаль в виде.

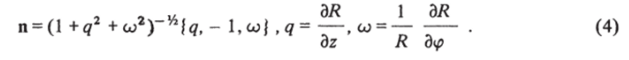
Рассмотрим некоторые частные примеры. Если рассматривается известная граничная поверхность, например, обтекаемое тело, то выполнение условий (1)-(3) очевидно, так как (4) получаются дифференцированием функций R (z, ф).

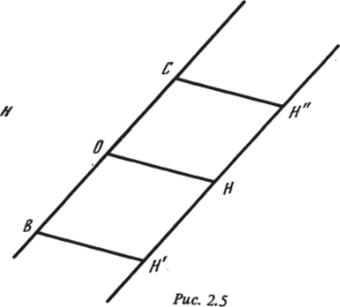
В случае неявных разностных схем [28, 29], в частности, полухарактеристических методов, составляющая со// нормали в точке // (рис. 2.5) вычисляется по формулам типа.

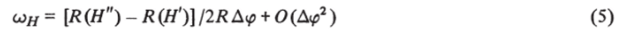
и в качестве неизвестной останется q_H. При этом равенство вторых смешанных производных с необходимой точностью выполняется и в разностной форме:

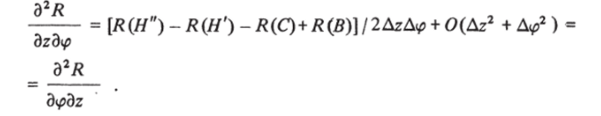
Для осесимметрических (плоских) поверхностей (линий) 0 и неизвестной в точке Н остается лишь q_H.

2. Докажем, что при построении разностных схем для нахождения и расчета точек свободной поверхности и ударной волны нельзя привлекать более одной линейной комбинации исходных уравнений (1.2), содержащей выводящие из рассчитываемой поверхности производные. Отсюда будет следовать некорректность предложенного в [24, 34, 33, 40] использования двух характеристических соотношений для расчета точек на заранее неизвестных граничных поверхностях.

Пусть ВОСН (рис. 2.4) является элементом искомой свободной поверхности, на которой должны выполняться граничные условия р = р₀ =const, Vn = 0.

При расчете геометрических и газодинамических функций в точке Н надо найти 6 неизвестных: 0, у, р, S, q, со. На первый взгляд кажется, что для их нахождения можно использовать 4 уравнения (1.2) и два граничных условия. Однако оказывается, что разностная аппроксимация уравнений (1.2) и граничные условия не определяют однозначно все 6 неизвестные в расчетной точке Я. Действительно, пусть на плоскости 9* (рис. 2.4), содержащей векторы к₂ и к₃, заданы начальные данные. Согласно граничному условию вдоль свободной поверхности, kj 0 и в первое уравнение из (1.2) в разностной форме не войдут неизвестные в точке Я. Из остальных уравнений (1.2) можно определить 0, у, S, из граничных условий р, а для нахождения двух геометрических величин q и to имеется лишь одно условие Vn = 0. Можно показать, что одна из комбинаций (1.2) будет содержать только внутренние производные на поверхности, например, в направлениях ВС и OD. Недостающее условие и дает соотношение типа (5) в неявных [29, 39] или (2) в явных схемах.

Рассмотрим расчетную точку Я ударной волны. Из законов сохранения при переходе через скачок уплотнения составляющие нормали q и со, а также давление и энтропию можно выразить через 0 и у:

Соотношение (6) выражает геометрические величины через газодинамические параметры 0 и у. Формальными вкладками можно убедиться, что якобиан преобразования (6) отличен от нуля (qpOJy — q_y^p Ф 0), а также что Ф 0. Соотношения (7) (первое из них — аналог двумерной ударной поляры, второе — условие Гюгонио) выступают как граничные условия для уравнений (1.2) и могут быть выражены в дифференциальной форме:

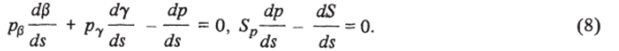
Здесь d/ds — производные, вообще говоря, в любом направлении на поверхности ударной волны.

Оказывается, что в трехмерном случае, кроме (8), между параметрами на ударной волне должна выполняться еше одна дифференциальная связь. Дифференцируя в (6) первое соотношение по у, а второе по z и учитывая д (сoR) дсо

тождество q^ =-= qco + R—, получим.

dz dz

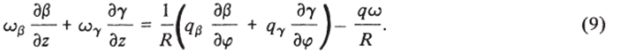
Это уравнение в осесимметричном или плоском случае выполняется тождественно (со = у = Ь0/дф =0). Аналогом граничного условия (9) в неявных разностных схемах является соотношение (5). Пусть в области BOCD плоскости пространственного типа [17] (рис. 2.4) известны начальные данные. Построим решение в близкой искомой точке Н ударной волны, проходящей через линию ВОС. Докажем, что при этом нельзя использовать более одной линейной комбинации уравнений газовой динамики (1.1) или (1.2).

Запишем уравнение (1.2) таким образом, чтобы они включали производные в направлениях $(0Я), l (OD), t (BC) (рис. 2.4), и разрешим их относительно производных по s (это всегда можно сделать, если плоскость № не является характеристической),.

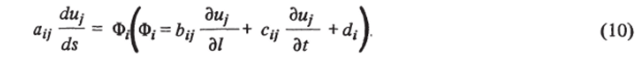
где I * 1, 2, 3, 4, и, = р, и₂ = у, и₃ = р, и₄ =S, а по повторяющемуся индексу / производится суммирование от 1 до 4.

Аналогично запишем уравнение (9) в виде.

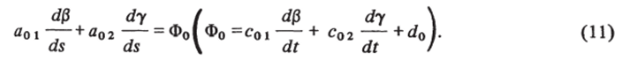
Отметим, что здесь Ф₀ Ф 0, с$ + Сог Ф 0. В самом деле, пусть существует такое направление на рассматриваемой поверхности, что (9) содержит производные лишь вдоль этого направления. Задавая это направление уравнением =.

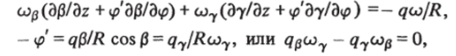
что противоречит условию невырожденности преобразования (6).

Рассмотрим уравнения (8), (10), (11) в окрестности точки О. Вычислим коэффициенты при производных и свободные члены этих уравнений по параметрам в точке О, а производные в правой части — по данным на плоскости 9^ъ • Параметры в точке Я можно найти, зная dtij/ds:

Затем по (6) можно определить q и ы в точке Я.

Таким образом, для четырех неизвестных dfi/ds, dy/ds, dp/ds, dS/ds имеем семь уравнений (8)-(11). Выбор из них четырех уравнений должен удовлетворять следующим условиям: выбранные условия линейно независимы и любое из уравнений (8), (11), вытекающих из граничных условий, либо используется непосредственно, либо является линейной комбинацией остальных уравнений. Первое условие очевидно. При невыполнении второго условия решение в точке Я не удовлетворяет всем граничным условиям.

Уравнения (8), (11) независимы между собой, например, отличны от нуля миноры третьего порядка в середине и справа соответствующей матрицы, равные соответственно а>₇(1 — S_p) иФ₀(1−5), так как со_у Ф 0 и Ф₀ Ф 0 согласно (7) и (11), aS_p Ф 1 (прир^ = 0, S = р~¹).

Покажем, что (11) нельзя получить линейной комбинацией уравнений (10). Аналогично можно доказать то же и для (8). Предположим противное. Пусть (11) является следствием уравнений (10). Тогда, в частности, справедливо равенство Ф₀ =а_|Ф₁ (а? + а! + <*1 + а& Ф 0). Так как в левой части этого равенства нет производных по /, а они зависят не только от данных вдоль ВОС, коэффициенты при duj/dl справа должны равняться нулю, т. е. biflg =0 (/ = 1, …" 4). Но это значит, что на ударной волне выполняется некоторая комбинация уравнений газодинамики (1.2), содержащая производные в двух направлениях — s (OH) и t (BC), т. е. ударная волна является характеристической поверхностью, что неверно. Следовательно, решение, полученное с использованием двух комбинаций (10), будет отличаться от решения с применением (11) на величины порядка [uj (D) — u,(0)](As/A 0″ т. е. при 0(Д$) = 0(А1) на величину О (As), тогда как согласно (12) это различие должно быть порядка О (As²).

Отсюда следует, что при использовании двух характеристических соотношений (двух комбинаций уравнений (1.2) или (10)) не выполняется уравнение (11). Этот факт сначала был обнаружен при практическом счете (см.: [43]). В этой же работе была доказана достаточность применнения одной бихарактеристики. Изложенное выше доказательство достаточности и необходимости получено позднее в работе [44].