Погрешности (ошибки) в анализе

С какой бы тщательностью ни проводилось то или иное количественное определение, полученный результат, как правило, несколько отличается от действительного содержания определяемого компонента, т. е. результат анализа всегда получается с некоторой неточностью — погрешностью.

Погрешности измерений классифицируют как систематические (определенные), случайные (неопределенные) и грубые или промахи.

Систематические погрешности — это погрешности, постоянные по значению или изменяющиеся по определенному закону. Они могут быть методическими, зависящими от особенности применяемого метода анализа. Они могут зависеть от применяемых приборов и реактивов, от неправильного или недостаточно тщательного выполнения аналитических операций, от индивидуальных особенностей человека, выполняющего анализ. Систематические погрешности трудно заметить, так как они постоянны и появляются при повторном определении. Чтобы избежать погрешностей такого рода, надо устранить их источник либо ввести соответствующую поправку в результат измерения.

Случайными погрешностями называют неопределенные по величине и знаку ошибки, в появлении каждой из которых не наблюдается какой-либо закономерности.

Случайные погрешности происходят при всяком измерении, и в том числе при любом аналитическом определении, как бы тщательно оно не проводилось. Наличие их сказывается в том, что повторные определения того или иного компонента в данном образце, выполненные одним и тем же методом, дают, как правило, несколько различающиеся между собой результаты.

В отличие от систематических погрешностей случайные не могут быть учтены или устранены введением каких-либо поправок. Однако они могут быть значительно уменьшены при увеличении числа параллельных определений. Влияние случайных погрешностей на результат анализа может быть учтено теоретически, путем обработки результатов, полученных в серии параллельных определений данного компонента, с помощью методов математической статистики.

Наличие грубых погрешностей или промахов проявляется в том, что среди сравнительно близких результатов наблюдается одно или несколько значений, заметно выделяющихся по величине из общего ряда. Если отличие настолько велико, что можно говорить о грубой ошибке, то это измерение сразу отбрасывают. Однако в большинстве случаев нельзя сразу признать тот иной результат неверным только по признаку «выскакивания» из общего ряда, и поэтому необходимо провести дополнительные исследования.

Бывают варианты, когда дополнительные исследования проводить нет смысла, и в то же время нежелательно использовать неверные данные для расчета общего результата анализа. В таком случае наличие грубых погрешностей или промахов устанавливают согласно критериям математической статистики.

Таких критериев известно несколько. Самым простым из них является Q-критерий.

Определение наличия грубых погрешностей (промахов) В химическом анализе содержание компонента в пробе устанавливают, как правило, по небольшому числу параллельных определений (n 3). Для расчета погрешностей определений в этом случае пользуются методами математической статистики, разработанными для малого числа определений. Результаты этого малого числа определений рассматривают как случайно выбранные — выборку — из всех мыслимых в данных условиях результатов генеральной совокупности.

При малых выборках с числом измерений n<10 определение грубых погрешностей можно оценивать при помощи размаха варьирования по Q-критерию. Для этого составляют соотношение:

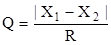
(13).

где Х₁ — подозрительно выделяющийся результат анализа;

Х₂ — результат единичного определения, ближайший по значению к Х₁;

R — размах варьирования — разница между наибольшим и наименьшим значением ряда измерений, т. е. R = Х_макс. — Х_мин.

Вычисленное значение Q сопоставляют с табличным значением Q (р, f). Наличие грубой погрешности доказано, если Q > Q (р, f).

Результат, признанный грубой погрешностью, из дальнейшего рассмотрения исключается.

Q-критерий — не единственный показатель, по значению которого можно судить о наличии грубой погрешности, но он рассчитывается быстрее других, т.к. позволяет сразу исключить грубые ошибки, не выполняя других расчетов.

Два других критерия более точные, но требуют полного расчета ошибки, т. е. о наличии грубой ошибки можно сказать, только выполнив полностью математическую обработку результатов анализа.

Грубые ошибки также можно определить:

А) По стандартному отклонению. Результат X_i признают грубой ошибкой и отбрасывают, если.

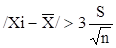
. (14).

Б) Точности прямого измерения. Результат X_i отбрасывают, если.

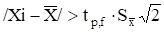
. (15).

О величинах, обозначенных знаками, речь идет в разделе 1.8.2.

Статистическая обработка результатов анализа Статистическая обработка результатов преследует две основные задачи.

Первая задача заключается в том, чтобы представить результат определений в компактной форме.

Вторая задача — оценить надежность полученных результатов, т. е. степень их соответствия истинному содержанию определяемого компонента в образце. Эта задача решается путем расчета воспроизводимости и точности анализа по формулам, приведенным ниже.

Как уже было отмечено, воспроизводимость характеризует разброс повторных результатов анализа и обуславливается наличием случайных погрешностей. Воспроизводимость анализа оценивается значениями стандартного отклонения, относительного стандартного отклонения, дисперсии.

Общая характеристика рассеяния данных определяется величиной стандартного отклонения S.

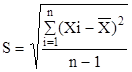
(16).

Иногда при оценке воспроизводимости анализа определяют относительное стандартное отклонение Sr.

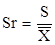
(17).

Стандартное отклонение имеет ту же единицу измерения, что и среднее, или истинное значение определяемой величины.

Метод или методика анализа тем лучше воспроизводимы, чем меньше для них значения абсолютного (S) и относительного (Sr) отклонения.

Рассеяние данных анализа относительно среднего значения рассчитывают как дисперсию S².

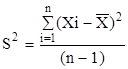
(18).

В представленных формулах: Xi — отдельное значение величины, полученное при выполнении анализа; - среднеарифметическое из результатов, полученных при всех измерениях; n — количество измерений; i = 1… n.

Правильность или точность анализа характеризуют доверительным интервалом среднего значения _{р, f}. Это область, внутри которой при отсутствии систематических погрешностей находится истинное значение измеряемой величины с доверительной вероятностью Р.

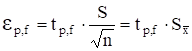
(19).

где _{р, f} — доверительный интервал, т. е. доверительные границы, в пределах которых может заключаться значение определяемой величины Х.

В этой формуле t_{р, f} — коэффициент Стьюдента; f — число степеней свободы; f = n — 1; Р — доверительная вероятность (см. 1.7.7); t_{р, f} — данное табличное.

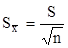
— стандартное отклонение среднеарифметического. (20).

Доверительный интервал рассчитывают либо в виде абсолютной погрешности в тех же единицах, в которых выражается результат анализа, либо в виде относительной погрешности Х_о (в%):

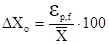
. (21).

Следовательно, результат анализа может быть представлен в виде:

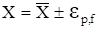
; (22).

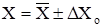
. (23).

Обработка результатов анализа значительно упрощается, если при выполнении анализов (контрольных проб, или стандартных образцов) известно истинное содержание () определяемого компонента. Вычисляют абсолютную (Х) и относительную (Х_о, %) погрешности.

Х = Х — (24).

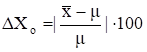
(25).

Сравнение двух средних результатов анализа, выполненного разными методами На практике бывают ситуации, когда объект необходимо анализировать разными методами, в разных лабораториях, разными аналитиками. В этих случаях получаются средние результаты, отличающиеся друг от друга. Оба результата характеризуют некоторое приближение к истинному значению искомой величины. Для того, чтобы выяснить, можно ли доверять обоим результатам, определяют, является ли разница между ними статистически значимой, т. е. «слишком» большой. Средние значения искомой величины считаются совместимыми, если они относятся к одной генеральной совокупности. Решить это можно, например, по критерию Фишера (F-критерию).

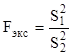
(26).

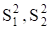
где — дисперсии, рассчитанные для разных серий анализов.

F_экс — всегда больше единицы, т.к. он равен отношению большей дисперсии к меньшей. Вычисленное значение F_экс сравнивают с табличным значением F_табл. (доверительная вероятность Р и число степеней свободы f для экспериментальных и табличных значений должны быть одинаковыми).

При сравнении F_экс и F_табл возможны варианты.

А) F_экс >F_табл. Расхождение между дисперсиями значимо и рассматриваемые выборки отличаются по воспроизводимости.

Б) Если F_экс значительно меньше F_табл, то различие в воспроизводимости имеет случайный характер и обе дисперсии являются приближенными оценками одной и той же общей для обеих выборок дисперсии генеральной совокупности.

Если расхождение между дисперсиями незначительно, можно выяснить, есть ли статистически значимая разница в средних результатах анализа, полученных разными способами. Для этого используют коэффициент Стьюдента t_{р, f}. Рассчитывают средневзвешенное стандартное отклонение и t_экс.

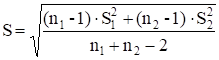
; (27).

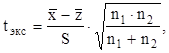
(28).

где — средние результаты сравниваемых выборок;

n₁, n₂ — число измерений в первой и второй выборках.

Сравнивают t_экс с t_табл при числе степеней свободы f = n₁+n₂-2.

Если при этом t_экс > t_табл, то расхождение между значимо, выборки не принадлежат одной генеральной совокупности и истинные значения в каждой выборке разные. Если t_экс < t_табл, можно все данные рассматривать как единую выборочную совокупность для (n₁+n₂) результатов.