Качественный анализ простейшей модели иммунного ответа на вирусную инфекцию

В настоящем подразделе будут приведены некоторые результаты исследования свойств решений системы уравнений простейшей модели, позволяющие анализировать ее адекватность рассматриваемому явлению. Параллельно будет даваться биологическая интерпретация математических результатов. Приведем для удобства обсуждаемую систему уравнений, записанную для временнбго интервала [0, т]:

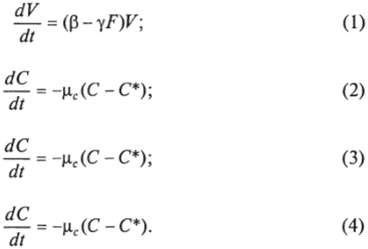
Прежде всего неотрицательность начальных условий (5) в подразд. 4.4 влечет за собой неотрицательность решений системы уравнений (1) —(4) для всех ?>0. Действительно, из уравнения (1) простейшей модели сразу следует.

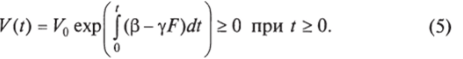
Для исследования решений F (t), C (t) и m (t) разобьем временной промежуток на интервалы [ят, (и + 1) т], где я = 0, 1, 2,… На первом интервале [0, т ] рассмотрим уравнение (2) и предположим, что утверждение о положительности С (1) неверно. Тогда в силу непрерывности решений должен существовать момент времени t_h при котором.

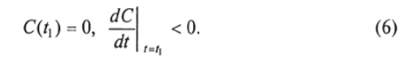
Но из уравнения (2) имеем.

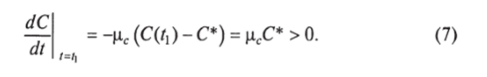
Получилось противоречие. Аналогично доказывается неотрицательность F (t) и m (t) на интервале [0, т]. Далее, учитывая, что на интервале [т, 2т] V (t- т) > 0, F (t — т) > О, устанавливаем неотрицательность решений на интервале [т, 2т]. Продолжая такие же рассуждения на последующие интервалы, по индукции устанавливаем сформулированный результат.

Аналогично предыдущему доказывается, что при С₀ > С* для всех t > 0 справедливо неравенство С (/) > С*. Неотрицательность решений модели соответствует биологическому смыслу описываемых ею процессов, так как эти решения интерпретируются как концентрации веществ, которые не могут быть отрицательными величинами.

Неотрицательность решений системы уравнений простейшей модели при всех t > 0 позволяет доказать их единственность.

Система уравнений простейшей модели (1) —(4) из подразд. 4.4 имеет два типа стационарных решений при ?(m) = 1:

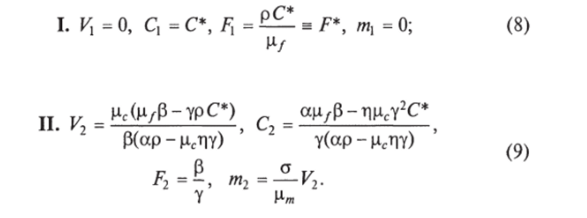
Решение (8) характеризует состояния здорового организма, так как V_x = 0, /и, = 0. Решение (9) интерпретируется как хроническая форма болезни при V₂ > 0. Достаточным условием положительности решения (9) является выполнение одной из систем неравенств:

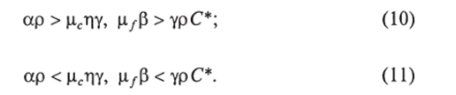
Достаточным условием асимптотической устойчивости стационарного решения (7) является выполнение неравенства р < yF*. Это означает следующее. При заражении здорового организма малой дозой вирусов отклоняющейся от стационарного значения величиной при / = 0 будет только У₀. При этом С₀ = С*, F₀ = F*, mo = 0. При достаточно малой дозе заражения в условиях Р > уF*, а именно, при выполнении условия.

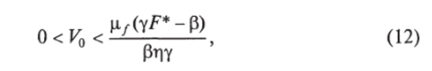
V (t) убывает на интервале [0, При этом функция V (t) удовлетворяет неравенству.

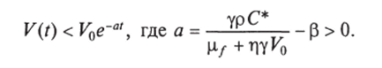
Эти результаты означают, что при выполнении неравенства (12) наступает выздоровление, независимо от дозы заражения.

Анализ стационарного решения (10), соответствующего хронической форме болезни, оказывается гораздо более трудоемким и не приводит к результатам, имеющим такую же четкую биологическую интерпретацию, как стационарное решение (8).

Исследование простейшей модели вирусного заболевания позволяет судить о качественном поведении концентрации вирусов V (t) при том или ином наборе коэффициентов. Удобно рассмотреть сначала два предельных случая, которые на самом деле являются границами для решения V (t).

Предположим, что организм не производит антител данной специфичности. Это означает, что F (t) = F₀ = 0 для всех / >0 и р = 0. Уравнение для V (t) в этом случае имеет вид.

а его решение дается выражением.

Динамика поражения органа вирусами описывается следующим уравнением:

решение которого при = 0 имеет вид.

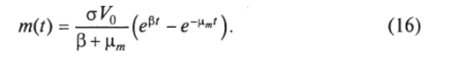
При отсутствии восстановительных процессов в пораженном органе, т. е. при =0, из (15) имеем.

и при всех / > 0 справедливо F{t) = 0. Такое решение соответствует течению болезни с летальным исходом. Этот предельный случай является хорошим приближением при слабом ответе иммунной системы на инфекцию.

Второй предельный случай реализуется при сильно выраженном иммунном ответе, когда уровень имеющихся в организме антител оказывается достаточно большим для того, чтобы уничтожить все проникшие в организм вирусы без включения меха

низма образования антител. В этом случае уравнение для V (t) имеет вид где Р у F.

Считая дозу заражения У₀ достаточно малой, можно считать F постоянной величиной, равной нормальному уровню антител F*. Тогда уравнение (18) переписывается в виде.

решение которого есть функция.

В предельном случае (р = 0) имеем.

При заданных значениях коэффициентов в уравнениях модели и произвольных начальных условиях все семейство разнообразных картин заболевания уложится в заштрихованной области, показанной на рис. 4.12.

Рассмотрим теперь поведение решений уравнений модели в случае, когда Р > уF* и в момент времени t = 0 происходит заражение здорового организма некоторой дозой вирусов V_Q > 0. Начальные условия выберем в виде:

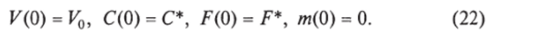
Концентрация вирусов при / > 0 начинает расти, так как вблизи точки / = 0, dV/dt > 0 в силу условия р > уF*. В некоторый мо.

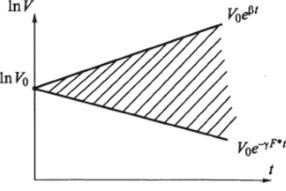
Рис. 4.12.

мент времени г, концентрация вирусов V (t) достигает максимума, причем в этой точке F (t) — Р/у. При />/, по смыслу модели F (t) превосходит уровень р/у и концентрация вирусов К (/) убывает, пока выполняется условие F (0 > Р/у, так как теперь dV/dt < 0. Здесь возможны две различные ситуации. Если F (t) > р/у на достаточно большом интервале времени (/, t₂) и V (t) на этом интервале падает практически до нуля, то реализуется острая форма болезни (рис. 4.13).

Если временной интервал (г_ь /₂) достаточно мал, то в точке h = F (t₂) = P/y и V (t) достигает минимума V_min, не успевая упасть до очень малых значений, а при / > /₂ функция V (t) вновь начинает расти, так как dV/dt > 0 при / = t_x + е (е > 0) вследствие того, что F (t) < р/у. В дальнейшем качественная картина не меняется и идет чередование локальных максимумов и минимумов V (t). Это хроническая форма болезни (рис. 4.14).

Биологическое следствие из приведенных результатов заключается в том, что хроническая форма болезни обусловлена недостаточно эффективной реакцией иммунной системы организма. При слабой реакции иммунной системы (что выражается в малом коэффициенте а, большом времени запаздывания т, значительном поражении органа) повышается значение К_тах и понижается значение F_m2X, что приводит к сужению интервала (/, /₂).

Аналогичным образом могут быть качественно проанализированы и другие ситуации, отличающиеся друг от друга значениями определенных комбинаций из констант, фигурирующих в уравнениях модели. Вычислительный эксперимент, для проведения которого уравнения модели целесообразно записать в безразмерном виде, позволил подтвердить и существенно детализировать результаты качественного анализа модели. Кроме того, оказалось возможным сделать ряд предсказаний о целесообразных формах лечения, которые были подтверждены клинической практикой. Одним из наиболее интересных предсказаний явилось обнаружение эффективного способа лечения хронической формы болезни путем ее искусственного обострения.

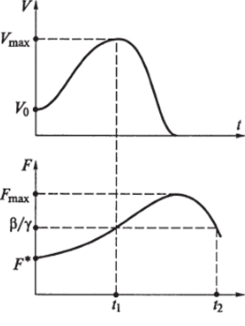
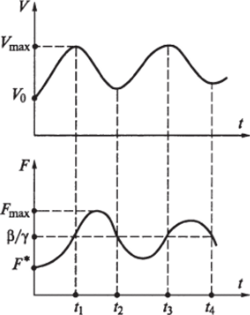
Рис. 4.13 Рис. 4.14.

В рамках простейшей модели иммунного ответа оказалось возможным исследовать влияние температурной реакции организма на динамику заболевания. Повышение температуры уменьшает эффективный коэффициент размножения вирусов и одновременно с этим стимулирует синтез белков в организме. Кроме того, с повышением температуры увеличивается скорость миграции вирусов и лимфоцитов, что повышает вероятность встречи между ними.

При учете температурной реакции организма уравнения простейшей модели сохраняют свой вид, только коэффициенты Р в первом уравнении для Ки, а во втором уравнении для С считаются функциями температуры Т, для которых используются следующие модельные выражения:

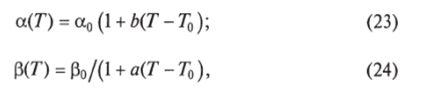
где Т₀ = 36,6 °С; а и b — константы, определяемые экспериментально.

К системе четырех уравнений модели добавляется пятое, описывающее изменение температуры:

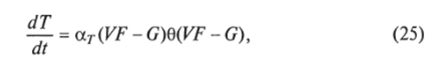aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">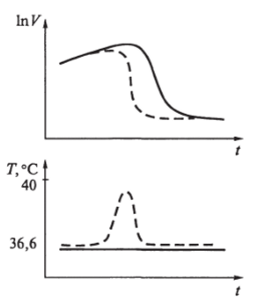

Рис. 4.15.

где G — максимально допустимая концентрация PF-комплексов, еще не стимулирующая повышение температуры. На рис. 4.15 показаны результаты численных экспериментов для рассматриваемого случая для определенного набора значений параметров модели. Сплошные линии соответствуют острой форме болезни с выздоровлением. Пунктирные линии соответствуют учету температурного эффекта.

Полученные результаты означают, что в рассмотренной модели температурная реакция является важнейшим механизмом самозащиты и самоизлечения организма.

Подводя итог обсуждению свойств простейшей модели иммунного ответа, отметим, что модель не описывает какое-то конкретное заболевание, но она позволяет найти и описать наиболее общие закономерности, присущие инфекционным заболеваниям. В этом смысле, как следует из приведенного далеко не полного перечня результатов, модель оказалась весьма эффективной.

Задачи и упражнения

• 1. Проведите рассуждения, аналогичные приведенным в тексте, доказывающие неотрицательность решений системы (1) —(4) на интервале [т, 2т].
• 2. Покажите, что соотношения (8) и (9) определяют стационарные решения системы (1) —(4).
• 3. Покажите, что уравнение (16) является решением уравнения (15) при начальном условии = 0.
• 4. Поясните характер и условия протекания процессов, показанных на рис. 4.13 и 4.14.
• 5. Поясните смысл уравнения (25), описывающего температурную реакцию на вирусную инфекцию.