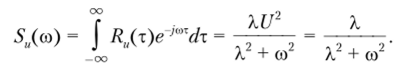Закон распределения Пуассона

В системах связи сталкиваются с распределением случайных целочисленных дискретных величин, представляющих собой последовательность точек, расположенных случайным образом. Такие точки могут соответствовать различным событиям, например моментам времени поступления заявок или наступления отказов в системе и др. Точечный случайный поток может встречаться и в задаче распределения вызовов на телефонной станции в течение суток. Для каждого интервала Т путем наблюдений можно установить среднее число вызовов XT (математическое ожидание). Коэффициент пропорциональности X характеризует интенсивность телефонных вызовов (среднее число вызовов в единицу времени). Вероятность появления п вызовов Р_т(п) на некотором интервале времени (О, Т) чаще всего определяется распределением Пуассона¹

Такое распределение задают только параметром закона Пуассона X — некоторой положительной величиной, значение которой равно среднему значению случайных величин распределения и одновременно равно дисперсии распределения. Для распределения Пуассона D_u = X, а_п = у/Х.

Сумма всех плотностей вероятностей для распределения Пуассона.

(здесь учтено, что в скобках записано разложение в ряд Тейлора функции е^х при х = X).

Графически закон распределения Пуассона удобно представлять многоугольником (полигоном) — ломаной линией, соединяющей точки с координатами (п, Pj). Па рис. 3.8 приведены многоугольники для случайной величины X, имеющей распределение Пуассона с параметром X = 0,5; Г, 2; 3,5; 5.

Условия справедливости распределения Пуассона достаточно просты.

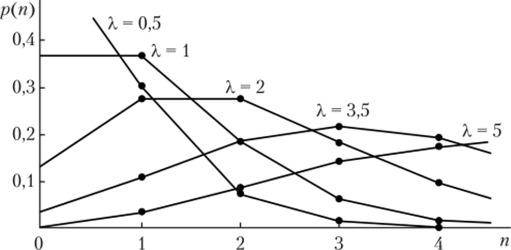
Рис. 3.8. Распределение Пуассона для ряда параметров X.

• 1 Симеон Дени Пуассон (5. Poisson, 1781 — 1840) — выдающийся французский математик, механик и физик.
• 1. Случайная величина может принимать только нулевые и целые положительные значения (как, например, число отказов аппаратуры или телефонных звонков за определенный интервал времени).
• 2. Вероятность отдельного события на бесконечно малом интервале времени счета событий пропорциональна величине этого интервала и при его стремлении к нулю также стремится к нулю как бесконечно малая первого порядка, а вероятности событий более высокой кратности (два события и более) стремятся к нулю как бесконечно малые более высоких порядков.
• 3. События в ненерекрывающихся интервалах времени их счета статистически независимы.

Пример 3.1.

Пример 3.1. Найдем плотность вероятности, математическое ожидание, дисперсию, корреляционную функцию и спектральную плотность случайного процесса U (t) вида телеграфного сигнала, реализация которого u (t) показана на рис. 3.9.

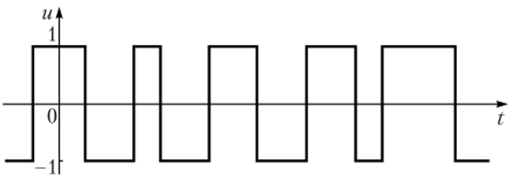
Рис. 3.9. Реализация случайного телеграфного сигнала

Решение

В теории связи таким телеграфным сигналом называют случайный процесс, реализации u (t) которого принимают значения уровней ?/=+1и?/=-1, причем «опрокидывания» уровня происходят в случайные моменты времени и число п «опрокидываний» уровня, происходящих за некоторый период Г, является случайной величиной с дискретным распределением вероятности, описываемым законом Пуассона.

Для данного случайного процесса в соотношении (3.10) параметр X — коэффициент, определяющий среднюю частоту возникновения изменения полярности сигнала в единицу времени; Р^п) — вероятность того, что за период Т произойдет п изменений полярности; при этом Р (1) = Р (-1) = 0,5.

Скачки уровня сигнала происходят в случайные моменты времени, поэтому аналитически записать отдельную реализацию данного случайного процесса оказывается весьма затруднительно. Конкретную реализацию случайного процесса удобно задать бесконечным множеством случайных величин ±1 — моментов изменения уровня, а характеристики случайного процесса определять их статистическими свойствами.

• 1. Плотность вероятности Р (п) = Р ( 1) + Р (-1) = 1.
• 2. Математическое ожидание т_и = 0, что очевидно из графика реализации.
• 3. Дисперсия

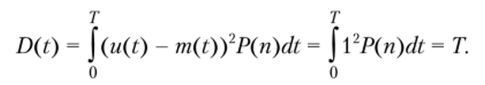
4. При вычислении корреляционной функции телеграфного сигнала каждое отдельное произведение u_k(t)u_k(t + т) равно либо U² = 1, либо -if = -1 в зависимости от совпадения или несовпадения знаков u_k(t) и u_k(t + т), причем вероятность значения корреляционной функции U² = 1 равна сумме «четных» вероятностей Р (0) + Р (2) + Р (4) + а вероятность корреляционной функции —U² = -1.

определяют суммой «нечетных» вероятностей Р (1) + Р (3) + … Следовательно,.

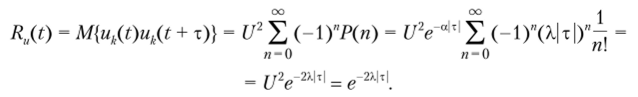
Параметр X полностью определяет корреляционные и спектральные свойства телеграфного сигнала, приведенные на рис. 3.10, а. При X —? 0 характеристики сигнала приближаются к характеристикам постоянной составляющей, при X —* оо — к характеристикам белого шума.

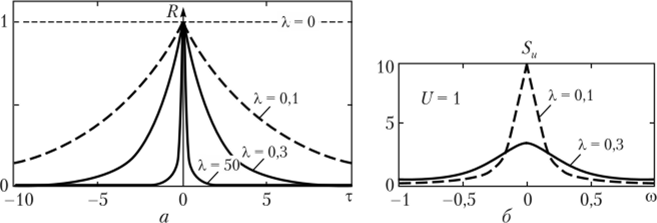
Рис. 3.10. Характеристики телеграфного сигнала:

а — функция корреляции; б — спектральная плотность Можно показать, что чем больше X, тем меньше время корреляции. При X —* 0 процесс вырождается в детерминированный (стремится к постоянной составляющей). При X —* оо процесс вырождается в белый шум с некоррелированными отсчетами на соседних точках времени.

5. Спектральная плотность телеграфного сигнала (рис. 3.10, б)