Некоторые сведения из теории уравнений в частных производных

Постановку задач для уравнений математической физики дадим на основе классических уравнений параболического, гиперболического и эллиптического типов.

| Основные определения Еслцискомая функция зависит не от одной, а от нескольких переменных, то при рассмотрении многих важных задач возникают уравнения с частными производными, связывающие между собой независимые переменные x_v х₂… х_к, а также искомую функцию и (х, х₀, …, х_и) и ее частные производные ,.

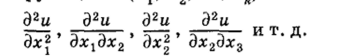
В общем случае уравнение в частных производных может быть записано в виде.

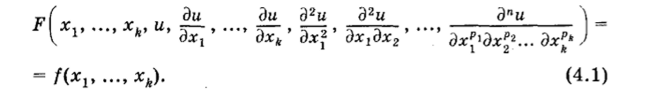
Здесь р_г + р₂ + … + р_к = п. Наивысший порядок входящей в дифференциальное уравнение производной называется ПОРЯДКОМ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ.

Если функция F линейна относительно функции и и ее производных, то уравнение (4.1) называется ЛИНЕЙНЫМ уравнением в частных производных. Если f (x_v …, х_к) ф 0, то уравнение (4.1) называется НЕОДНОРОДНЫМ, а если f (x_v …, х_к) = 0, то ОДНОРОДНЫМ.

Если функция F линейна по высшим производным (n-го порядка), т. е. коэффициенты при высших производных могут зависеть лишь от функции и и производных до (п — 1)-го порядка, то дифференциальное уравнение называется КВАЗИЛИНЕЙНЫМ.

КЛАССИЧЕСКИМ РЕШЕНИЕМ называется функция u (x_v … х_к), имеющая частные производные до требуемого порядка и обращающая уравнение (4.1) в тождество. Решение уравнений с частными производными, как правило, не единственно. Если в случае обыкновенного дифференциального уравнения общее решение зависит от конечного числа параметров, то для уравнений в частных производных обычно имеется общее решение, зависящее от производных функций с числом аргументов на единицу меньше, чем у функции «(*, х_к). Например, уравнение.

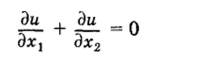
имеет решение, зависящее от произвольной функции.

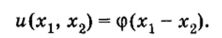
Таким образом, так же как и для обыкновенного дифференциального уравнения, для выделения единственного решения необходимо задавать дополнительные условия, в которые будут входить функции с числом аргументов k — 1. В качестве таких условий можно потребовать, чтобы искомая функция и (х_х, … х_к) принимала заданные значения на поверхности размерности k — 1 в пространстве переменных x_v х₂, …, х_к. К этому типу условий относятся начальные и граничные условия, являющиеся наиболее часто встречающимися при постановке краевых задач математической физики.

Уравнения математической физики Рассмотрим классические уравнения математической физики. В этих уравнениях в качестве независимых переменных присутствуют время t и пространственные координаты: декартовы, цилиндрические и сферические.

Задача называется СТАЦИОНАРНОЙ, если решение не зависит от времени, и НЕСТАЦИОНАРНОЙ или ЭВОЛЮЦИОННОЙ, если оно зависит от времени. Задачи с одной пространственной переменной называются одномерными, с двумя — двумерными, с тремя — трехмерными.

Приведем каноническую форму уравнений с двумя независимыми переменными^[1]. Пусть.

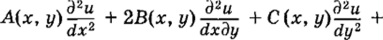
— уравнение с дважды непрерывно дифференцируемыми коэффициентами А, В, С, которые не обращаются в нуль одновременно. Приведем классификацию дифференциальных уравнений в частных производных. Обозначим D = В² — АС, тогда при D = О уравнение (4.2) называется ПАРАБОЛИЧЕСКИМ, при D > 0 — ГИПЕРБОЛИЧЕСКИМ, а при D < 0 — ЭЛЛИПТИЧЕСКИМ дифференциальным уравнением. Тип одного и того же уравнения может меняться в зависимости от области пространства.

Классическим уравнением гиперболического типа является волновое уравнение, параболического типа — уравнение теплопроводности, а эллиптического типа — уравнение Лапласа.

В математической физике различают задачу Коши (или задачу с начальными данными); краевые или граничные задачи; смешанные краевые задачи или краевые (граничные) задачи с начальными данными. Задачи, в которых в качестве переменной выступает время 1, иногда называют эволюционными.

В теории уравнений в частных производных важную роль играют характеристические поверхности, которые определяются как поверхности, в окрестности которых решения задачи Коши не существует, либо решение это не единственно. Можно показать, что в действительной плоскости характеристические поверхности существуют для гиперболических и параболических уравнений и не существуют для эллиптических уравнений.

Общая теория характерик позволяет сформулировать для гиперболических уравнений некоторые специфические задачи такие, как задача Гурса, смешанная задача и ряд других. Их решение можно построить, используя как аналитический, так и численный методы характеристик.

Постановка задан для уравнений параболического типа Классическим примером уравнения параболического типа является УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИ или ДИФФУЗИИ в области [О, I] на отрезке времени 10, 1] (рис. 4.1).

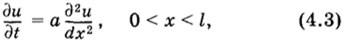
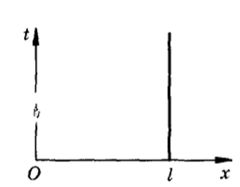
где а — коэффициент теплопроводности (если и — температура) и массопроводности (если и — концентрация, давление в задачах фильтрации и т. п.). Поскольку в уравнение (4−3) входит производная по времени, то необходимо зада- Рис. 4.1 вать начальные условия при t = 0 и граничные условия при х ~ 0, х — t > 0.

Для уравнения теплопроводности при краевых условиях.

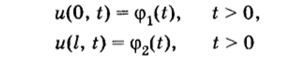
и начальном условии.

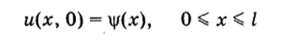
имеем ПЕРВУЮ НАЧАЛЬНО-КРАЕВУЮ или КРАЕВУЮ ЗАДАЧУ С НАЧАЛЬНЫМИ ДАННЫМИ — иначе, задачу Коши с краевыми (граничными) условиями.

Для уравнения теплопроводности с краевыми условиями 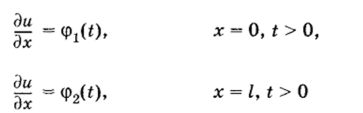и начальными данными.

имеем ВТОРУЮ КРАЕВУЮ ЗАДАЧУ С НАЧАЛЬНЫМИ ДАННЫМИ. Для уравнения теплопроводности с краевыми условиями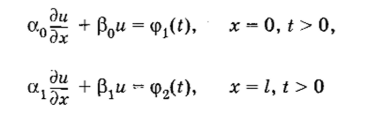

и начальными условиями.

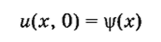
имеем ТРЕТЬЮ КРАЕВУЮ ЗАДАЧУ С НАЧАЛЬНЫМИ ДАННЫМИ.

В бесконечной области ставится следующая ЗАДАЧА КОШИ для уравнения теплопроводности:

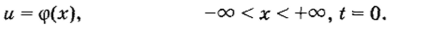
Постановка задач для уравнений гиперболического типа Классическим примером уравнения гиперболического типа является ВОЛНОВОЕ УРАВНЕНИЕ.

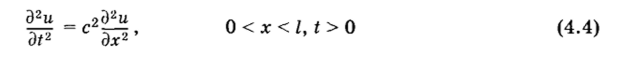
или более общее, описывающее малые продольные колебания стержня и поперечные колебания струны. Здесь функция и (х, t) характеризует отклонение струны от положения равновесия, а параметр с — скорость распространения возмущений. К волновому уравнению сводятся также уравнения распространения малых акустических возмущений.

Поскольку в уравнение (4.4) входит вторая производная по времени, старший порядок производной по времени в начальных условиях не превышает единицы. Тогда первая, вторая и третья начально-краевые или краевые задачи с начальными данными для волнового уравнения будут иметь соответственно следующий вид:

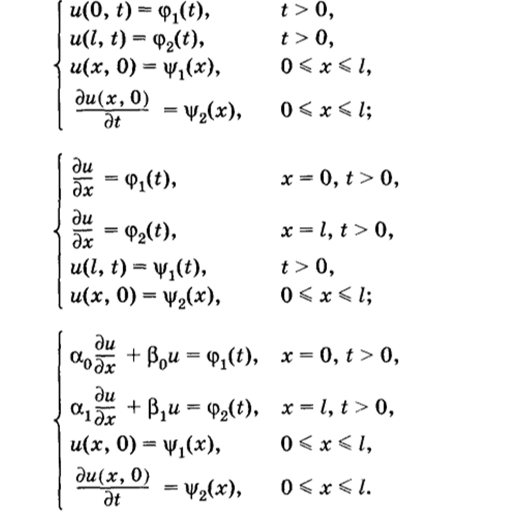
В бесконечной области можно поставить задачу Коши:

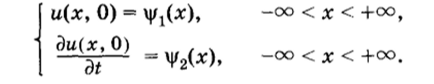
ПУАССОН СИМЕОН ДЕНИ (Poisson Simeon Denis; 1781 — 1840) — французский математик и механик, труды которого относятся к небесной механике, математике и математической физике. Получили известность его исследования об устойчивости движения планет Солнечной системы. В работах по теории притяжения П. вывел уравнение, носящее его имя. Собственно в математике П. обращался к определенным инте1ралам (интеграл Пуассона), уравнениям в конечных разностях (формула суммирования Пуассона), теории дифференциальных уравнений с частными производными, теории вероятностей. В гидромеханике П. обобщил уравнение Навье — Стокса на случай движения сжимаемой вязкой жидкости с учетом теплопередачи. Им решен ряд задач теории упругости и обобщены уравнения теории упругости на анизотропные тела. В сопротивлении материалов П. ввел коэффициент поперечной деформации |i, носящий в названии имя автора.

Метод характеристик позволяет решать задачи Коши, Гурса и смешанные при задании условий в ограниченной области.

Постановка задам для уравнений эллиптического вида Классическими примерами уравнений эллиптического типа являются УРАВНЕНИЕ ЛАПЛАСА.

И УРАВНЕНИЕ ПУАССОНА.

описывающие течение идеальной (без вязкости и теплопроводности) жидкости в стационарных потоках, стационарное распределение температуры, стационарное распределение напряженности электрического или магнитного полей. При этом уравнение (4.5) описывает все эти явления при отсутствии источников или стоков (нет правых частей), а уравнение (4.6) — с распределенными по области Q. источниками, задаваемыми правой частью fix, у) (рис. 4.2).

Поскольку уравнения (4,5), (4.6) — стационарные, то начальные условия не задаются; на границах же Г расчетной области Q + Г задаются граничные условия 1,.

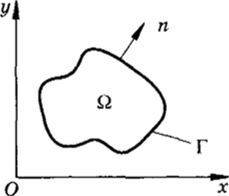
Рис. 4.2.

2 и 3-го родов.

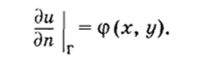
• Первая краевая задача для уравнения Лапласа (задача Дирихле):

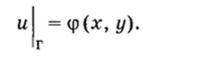
• Вторая краевая задача для уравнения Лапласа (задача Неймана):

НЕЙМАН КАРЛ ГОТФРИД (Neumann Karl Gottfried; 1832—1925) — немецкий математик, основные исследования которого относятся к теории логарифмического потенциала. Н. предложил метод (метод Неймана) решения задачи Дирихле для случая выпуклых контуров и выпуклых поверхностей. Н. исследовал вторую краевую задачу (задачу Неймана). Ему принадлежат также работы в области математической физики, теории функций Бесселя, римановой теории и абелевых интегралов.

• Третья краевая задача для уравнения Лапласа (смешанная задача):

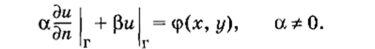
Во второй и третьей краевой задаче производные берутся в направлении внешней нормали по отношению к границе области ?2.

Постановка многомерных задам математической физики В заключение приведем примеры постановок многомерных по пространственным переменным задач для уравнений параболического и эллиптического типов (рис. 4.3).

• Первая начально-краевая задача для двумерного уравнения теплопроводности:

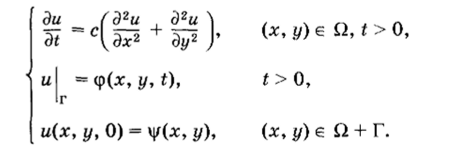
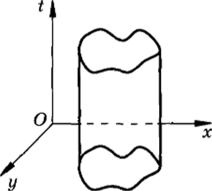
Рис. 4.3.

• Третья начально-краевая задача для двумерного уравнения теплопроводности:

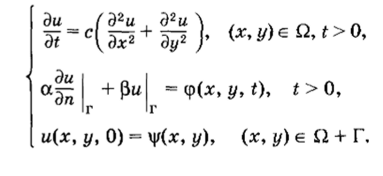
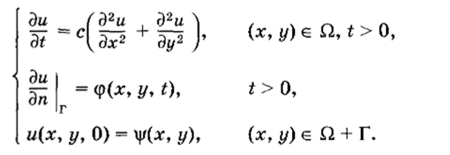
• Первая начально-краевая задача для двумерного волнового уравнения:

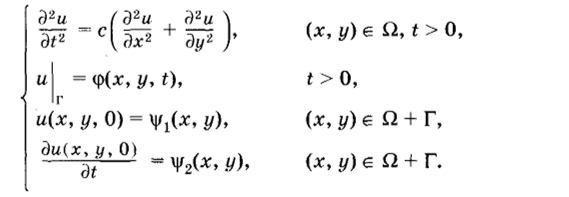
• Вторая начально-краевая задача для двумерного волнового уравнения:

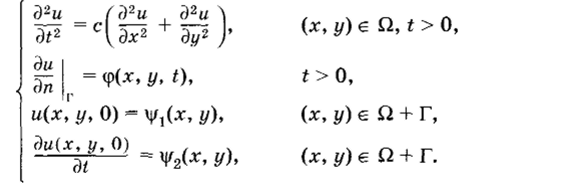
• Третья начально-краевая задача для двумерного волнового уравнения:

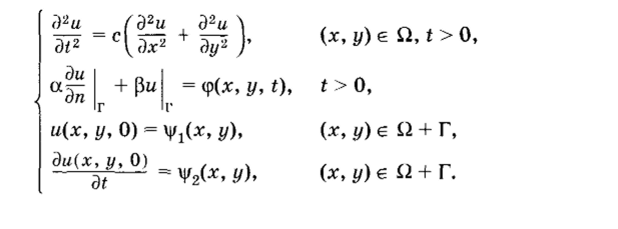
• [1] В общем случае для более чем двух независимых переменных таких канонических форм не существует.