Цветовые измерения и классификации

Цветовые модели не только классифицируют цвета, но и дают представление о цветовых смесях, а также позволяют осуществлять цветовые измерения в графической форме (по координатным осям). Цветовые измерения позволяют описать все цветовые оттенки для определения точных критериев их схожести и различия. Таким образом, цветовые измерения — это методы измерения и количественного выражения цвета. Вместе с различными способами математического описания цвета цветовые измерения составляют предмет колориметрий. В результате цветовых измерений вычисляются три числа, так называемые цветовые координаты, определяющие цвет (при некоторых строго стандартизованных условиях его рассматривания). Цветовые координаты показывают, к какой из групп спектральных составов, различимых визуально друг от друга, принадлежит измеряемое излучение.

Основой математического описания цвета в колориметрии является экспериментально установленный закон Грассмана^[1][2]: «для любых четырех цветов всегда существует связывающее их линейное соотношение, причем это соотношение будет единственным, если только какие-либо три цвета из этих четырех не связаны линейными соотношениями, причем, с другой стороны, можно найти бесчисленное множество троек цветов, которые никаким линейным соотношением не связаны»^[3].

Исходя из закона Грассмана, любой цвет можно представить в виде смеси (суммы) определенных количеств трех линейно независимых цветов. Линейно независимые цвета — это цвета, ни один из которых не может быть получен как сумма (или линейная комбинация) двух других. Систем линейно независимых цветов существует бесконечно много, но в колориметрии используются лишь некоторые из них. Три выбранных линейно независимых цвета называют основными цветами; они определяют цветовую координатную систему.

Таким образом, измеряемый цвет (вектор С) представляют как линейную комбинацию трех единичных векторов E_v Е_ъ Е₃ — основных цветов, образующих систему координат трехмерного цветового пространства. Результат измерения записывается в виде векторного цветового уравнения.

где щ, т₂, щ — отсчеты, но трем шкалам прибора, с помощью которого ведется измерение.

Суммирование цветовых векторов получается суммированием соответствующих излучений, а умножение на скаляр — соответственным изменением освещенности поля. Основные цвета прибора Е_{, Е₂, Е₃ являются, как это следует из уравнения, цветами фотометрического поля тогда, когда на трех шкалах прибора установлены отсчеты: [1; 0; 0] для ?, [0; 1; 0] для Е₂ и [0; 0; 1] для Е₃. Таким образом, цвет С подбирается смешением основных цветов прибора, а отсчеты щ, т₂, щ являются компонентами вектора С по системе единичных векторов Е, Е_2у Е₃.

Выбор системы координат (основных цветов прибора) произволен, однако часто используют три основных цвета из трехкомпонентной теории — красный (R), синий (В) и зеленый (G). Такая колориметрическая система называется системой RGB, и она является аддитивной. В таком случае уравнение (4.1) можно представить в виде.

где С — вектор в трехмерном пространстве; /?, G и В — его орты; r g b ' — координаты по трем осям.

Таким образом, для определения цвета необходимо указать три величины — его координаты в цветовом пространстве. Для системы RGB три оси координат R_y G и В образуют трехмерное пространство, где оси проведены из начала координат под любым углом друг к другу. Отложив по осям три координаты r g' и Ь можно определить точку в пространстве. Каждому цвету соответствует своя точка. Вся совокупность возможных цветов занимает некоторый объем, образуя цветовое тело. Все реально существующие цвета будут размещаться внутри некоторого выпуклого конуса с вершиной в начале координат (точка отсутствия цвета) и с неограниченными по длине образующими (рис. 4.13). Если в точку, изображающую цвет, провести прямую из начала координат, получится вектор. Представление цвета в виде вектора удобно тем, что цвета можно складывать, но правилу сложения векторов.

В настоящее время одной из наиболее распространенных цветовых моделей является барицентрическая модель (рис. 4.14), предложенная в 1931 г. Международной комиссией по освещению (МОК), которая и применяется с тех пор с небольшими изменениями. Эта модель предлагает более точные количественные методы описания цвета и различимости отдельных его оттенков по сравнению с цветовым кругом, что является наиболее актуальным для многих отраслей производства, в том числе для полиграфии и компьютерных технологий. Барицентрическая модель¹ позволяет изображать трехмерные векторы цвета точками на плоскости с приписанным этим точкам «весом» в качестве третьей координаты.

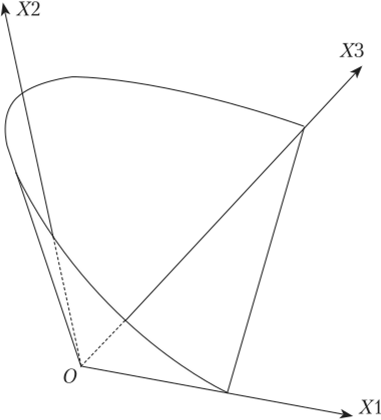
Рис. 4.13. Расположение цветов в пространстве:

0X1, 0X2, 0X3 — направления единичных векторов R, G, В

Модель МОК представляет собой треугольник XYZ, вершины которого соответствуют эталонным длинам волн, равным соответственно 700,0 нм (R — красный), 546,1 (G — зеленый) и 435,8 нм (В — синий). Выбранные стимулы удобны тем, что два из них (В и R) близки к краям видимого спектра, а третий (G) близок к его середине. Вся область представления цветов лежит внутри, между сторонами треугольника XYZ.

Связь барицентрической системы с обычной пространственной системой координат (рис. 4.13, формула (4.1)) определяется формулами:

где т_{, т₂, т₃ — компоненты вектора С в пространстве; хну — координаты точки С на плоскости треугольника XYZ q — «вес» этой точки^[4][5].

Из приведенных формул следует, что при пространственном сложении векторов в барицентрической системе суммарный вес равен сумме весов и расположен в центре тяжести складываемых весов. Геометрическое преобразование (4.3) представляет собой центральную проекцию цветового пространства из начала координат на плоскость, проведенную через концы единичных векторов пространственной системы координат (см. рис. 4.14).

Векторы одинакового направления, т. е. цвета одинаковой цветности, изображаются в плоскости треугольника той же точкой и различаются только весом.

Рис. 4.14. Барицентрическая модель: цветовой треугольник системы МОК RGB.

Барицентрическая система, как и пространственная, характеризует цвет с помощью трех координат и позволяет вести все цветовые расчеты. Например, даны два цвета F_{ и F₂, необходимо получить третий цвет С, являющийся смесью указанных двух: С = +F₂ (см. рис. 4.14). Цвета F_x

и F₂ изображены точками с координатами (0,2; 0,2) и (0,3; 0,6), в которых помещены веса q_x = 15 и q₂ = 5. Сумма С лежит в центре тяжести складываемых цветов (х_с = 0,225; у_с = 0,3) с весом qc = qi + = 20. Барицентрическая модель основывается на трехкомнонентном подходе и является стандартной системой для цветовых измерений. Однако кроме нее в науке существуют и другие системы, которые систематизируют цветовые оттенки по иному признаку. Одной из таких моделей является цветовое тело Оствальда^[6]. Система Оствальда широко используется в живописи и дизайне, но в настоящее время она представляет больше исторический интерес. Система Оствальда основана на теории оппонснтных цветов Геринга. Оствальд представил все цвета в виде замкнутого цветового тела, состоящего из двух конусов, объединенных общим основанием. Единой осью конусов является ахроматический ряд: верхняя точка — белый цвет, нижняя — черный. Для создания цветового основания конусов Оствальд использовал четыре геринговских базовых цветовых тона — синий, желтый, красный и зеленый, связав их прямой линией, проходящей через белую точку на цветовом круге (рис. 4.15). Цветовое тело Оствальда включает 1536 цветов, каждый из которых определяется через строгое соотношение белого и черного и имеет цифровое и буквенное обозначение.

Рис. 4.15. Цветовое тело Оствальда.

• [1] Колориметрия (от лат. color — цвет и греч. metreo — измеряю) — методы измеренияколичественного выражения цвета, основаны на определении координат цвета в выбраннойсистеме трех основных цветов.
• [2] Грассман Герман Гюнтер (1809—1877) — немецкий математик, физик и филолог. Далпервое систематическое построение учения о многомерном евклидовом пространстве. Разработал общую теорию действий над векторами, что привело его к открытию возможностирассматривать цветовые ощущения как трехмерные векторы, а это лежит в основе современного учения о цвете. Им установлены законы сложения цветов (1853).
• [3] Нюберг II. Д. Измерение цвета и цветовые стандарты. М.: Стандартизация и рационализация, 1933.
• [4] Эта же система в англоязычной литературе называется колориметрической системойCIE.
• [5] Герман фон Гельмгольц назвал эту координату количеством цвета.
• [6] Оствальд Фридрих Вильгельм (1853—1932) — немецкий физик и химик, философ-идеалист, лауреат Нобелевской премии по химии 1909 г. «за изучение природы катализаи основополагающие исследования скоростей химических реакций».