Релевантная логика в R.N-категориях

Трудности, возникающие на пути интерпретации в категориях предпорядка, связаны еще и с отличием в формулировке понятия импликации в неклассических логиках. Чтобы преодолеть эту трудность, прибегают к интерпретации импликации как резидуала относительно некоторой операции. Дело в том, что для большинства логических исчислений справедливо следующее утверждение: существует бинарная операция ®, такая, что для всех а, Ь, с, а®Ь < с тогда и только тогда, когда а<�Ь -" с.

При этом операция ® обычно соответствует некоторой логической связке (в частности, в случае классической и интуиционистской логик это конъюнкция), хотя в общем случае это необязательно.

В N-категориях роль резидуала выполняет относительное псевдодополнение, в случае же релевантной логики ситуация сложнее: операции ® здесь соответствует связка ° (совместимость или релевантная конъюнкция), которая хотя и производна, но ее алгебраическая модель — операция группоидного умножения. Поскольку алгебраические модели релевантной логики согласно [Максимова 1973] представляют собой т.н. стримтану, т. е. дистрибутивную решетку с резидуалом (импликацией) и дополнением, то возникает необходимость наделить N-категорию еще и структурой группоида.

Определение 1. R-категория С есть группоидная категория предпорядка, снабженная ковариантным бифунктором ®: СхС —"С, такая, что:

• (i) С имеет конечные произведения (-,-) и копроизведения [-, -];
• (ii) если а —> b есть стрелка в С, то, а ® х —>Ь®хнх®а—> х ® b есть стрелка в С для всех х из С;
• (ш) для любых x, y, z из С имеет место следующие естественные изоморфизмы:

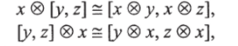
т.е. бифунктор сохраняет копроизведения;

• (iv) в С существует объект 1, такой, что 1 ®х = дгих->х®х есть стрелка в С для всех их С;
• (v) в С существуют резидуалы (с есть резидуал а относительно Ь, если следующее свойство имеет место: для любого х из С, х -" с есть стрелка в С тогда и только тогда, когда х® а b есть стрелка в С).

Будем обозначать наибольший резидуал а относительно Ь как а=>Ь. Нетрудно видеть, что резидуал => отличается от относительного псевдодополнения в N-категориях [Riscos Laita 1987, р. 507] тем, что псевдодополнение есть резидуал относительно произведений <-, -) в категориях предпорядка.

Определение 2. RN-категория есть R-категория, снабженная контравариантным функтором N: С —" С, таким, что:

(i) функтор № естественно эквивалентен тождеству в С, т. е.

N²a = а для любого объекта а из С;

(й) для любых а, Ь из С, (а => Nb)®b —> Na и а => Na -" Na суть стрелки в С.

RN-категория обладает следующими свойствами:

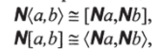
С дистрибутивна, т. е. [{а, Ь),{а, с)] = [а,{Ь, с)

Теорема 1. RN-категория является декартово замкнутой относительно бифунктора ® категорией.

Доказательство. Декартова замкнутость относительно бифунктора ® означает, что в диаграмме экспоненцирования вместо произведений фигурирует бифунктор ®, т. е. она выглядит следующим образом:

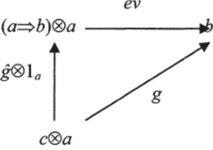
В качестве экспоненциала здесь выступает резидуал. Для стрелки g: с®а —> b стрелку g: с —> а=>Ь мы получаем из определения резидуала, а используя 1″: а -> а переходим к стрелке g®l". Рассмотрим теперь стрелку 1″: а => Ь —> а Ь. Из определения резидуала мы получаем стрелку (а => b)®a —> b которая и будет стрелкой ev, замыкая диаграмму. Поскольку конечная полнота следует из пункта (i) определения 1, то RN-категория будет декартово замкнутой относительно бифунктора ®. ?

В работе [Максимова 1973] пропозициональной регулярной логикой называется любое множество L с F_n (где F" - множество формул, содержащих конъюнкцию, дизъюнкцию и отрицание в качестве логических связок), удовлетворяющее условиям: для любых а, р, уе F"

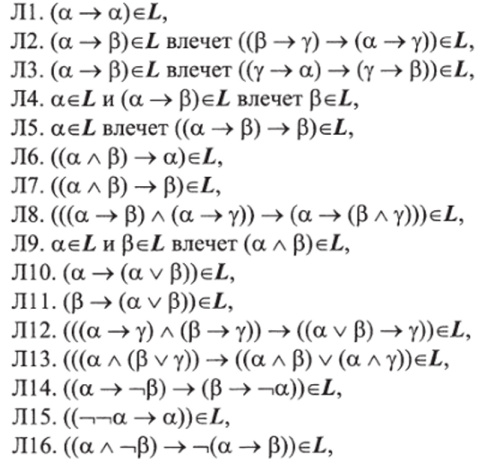
Л16. Если aeL и р есть результат подстановки некоторых формул вместо переменных в формулу а, то РeL.

Пропозициональное исчисление называется регулярным пропозициональным исчислением, если множество выводимых в этом исчислении формул составляет регулярную логику. Рассмотрим регулярные пропозициональные исчисления, в которых в качестве аксиом взяты одна или несколько следующих формул:

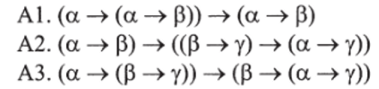
Регулярное пропозициональное исчисление с аксиомами А1 и А2 представляет собой исчисление со строгой импликацией. Добавляя сюда АЗ, мы получаем исчисление R релевантной импликации.

Словарь перевода высказываний в RN-категории будет представлять собой следующий список: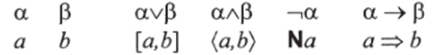

Если а есть перевод аксиомы или общезначимой релевантной формулы в RN-категорию С, то это означает, что 1 —>а есть стрелка в С. Однако по определению резидуала существование стрелки 1 —> а => b означает, что 1®а —> b есть стрелка в С. Поскольку же по (iv) 1®<�з = а, то отсюда следует, что если, например, перевод аксиомы А1 есть.

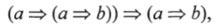
то это эквивалентно.

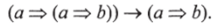
Применяя подобные преобразования к списку аксиом, мы получаем следующий список стрелок:

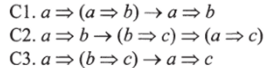
Условия С1-СЗ в чисто RN-категорном виде перепишутся следующим образом:

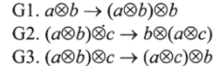
Что касается условий Л11 -Л 17, то их категорный перевод не приводит к каким-либо новым условиям на RN-категории, в чем легко можно убедиться, переводя на категорный язык соответствующие выкладки из [Максимова 1973, с. 452].

Определение 3. Пусть C_RN и С _RN будут RN-категориями (с бифункторами ® и ®' и функторами N и N' соответственно). RNфунктор F: C_R —" C_RN есть функтор, обладающий следующими свойствами (для a, b, 1 из C_Rn и 1' из С rn соответственно):

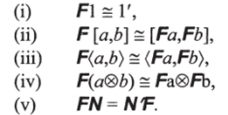
Доказательства следующих двух предложений получаются путем соответствующей категорной модификации алгебраических результатов из [Максимова 1973], основанных на понятии стримпланы, RPg-пространства и импликативно-негативного группоида.

Предложение 1. Каждая RN-категория имеет полное расширение (полнота означает здесь существование бесконечных произведений и копроизведений).

Набросок доказательства. Пусть, А будет RN-категорией и пусть Si будет множеством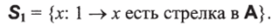

Рассмотрим множество С₀ фильтров на С, т. е. таких СсС, что.

• (a) если хе С и х -" у есть стрелка в С, то ye С;
• (b) С замкнуто относительно произведений, т. е. х, уеС влечет (х, у) еС.

Обозначим теперь через Ci семейство всех простых фильтров на С (т.е. таких С с Со, что если [х, у]еС, то хеС либо уеС). Пополняя Ci до С₂ = CiuC и определяя на С₂ стрелки как отношение включения, получаем категорию предпорядка С'. При этом множество будет плотным, что означает, что (Vx, yeC)(VweC₂)(w —> х®у есть стрелка в С, если ((БиеС₂)(и -зги w —> и®у есть стрелки в С) и (ЗуеСгХг —з у и w —) x®v есть стрелки в С])). Произведения и копроизведения на С определяются как пересечения и объединения простых фильтров, а отображение.

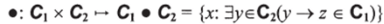
представляющее собой ковариантный бифунктор вместе с.

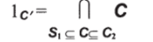
приводят к тому, что С' становится R-категорией. Чтобы превратить ее в RN-категорию, определяем отображение:

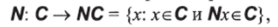
которое дает нам контравариантный N-функтор.

Таким образом, мы приходим к заключению, что полное расширение определяется нарами (q,С), где qeC и С есть простой ультрафильтр. ?

Предложение 2. Пусть C.B.S будут RN-категориями, где В есть расширение С и S есть полная категория. Любой RNфунктор F: С —" S может быть расширен до RN-функтора G: В > S.

Набросок доказательства. Определяем семейство пар (D.K), где О есть подкатегория В, а К есть RN-функтор, расширяющий G. Применяя лемму Цорна, получаем максимальный элемент (B'G). Если В * В' то возьмем ЬеВВ' и сконструируем В" = {[{b, p),(Nb, q)]: p. qeB'), которая будег представлять собой RNкатегорию, что входит в явное противоречие с максимальностью В' ([(b, p),(Nb, q)] = (brq)u (Nbr-q), т. е. опять простой ультрафильтр). ?

Далее везде Е будет означать RN-категорию.

Пусть р есть объект Е и пусть S_p обозначает категорию.

чьи стрелки те же, что ив Е. Если определить ®_р как ®_р: S_pxS_p->S_p посредством х®_ру = [х®у, р, то нетрудно видеть, что ®_р будет представлять собой ковариантный бифунктор, такой, что пара (S,"®_p) становится R-категорий с теми же произведениями и копроизведениями, что ив Е. Если же мы теперь определим N_p: S_p —> S_p как NpX = [Nx, p], то получим контравариантный функтор N_p и тройка (S_P,®_P, N_P) становится RN-категорией.

Пусть S будет непустым семейством элементов Е. Для п >2 определяем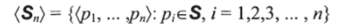

и определяем.

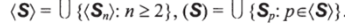
Отметим, что (S) здесь не что иное, как RN-категорный перевод простых фильтров в импликативных группоидах из [Максимова 1973].

Отношение ~s, определяемое как.

р~s <7 тогда и только тогда, когда р => q, q => р e (S), есть отношение конгруэнтности, приводящее нас к факторкатегории E/₍s). Если же мы определим в E/₍S).

INI —> lb’ll ^есть стрелка тогда и только тогда, когда х=>уе Е/₍$) то E/(S) становится категорией предпорядка. Если мы теперь определим ®s: E/(S) х E/(S) —> E/(S) посредством |NI®slWI ⁼ ||*®.И! ^и Ns E/_{s) —> E/(S) посредством N_sx = Nx, to ®_s и Ns суть ковариантный бифунктор и контравариантный функтор соответственно, а тройка (E/(S),®s, Ws) есть RN-категория с ||1|| в качестве левой единицы R-категории и произведениями (IMUMDs ⁼ 1Клг₁у)|| и копроизведениями [INI.IMI] ⁼ [х, у) соответственно.

Справедливо следующее предложение:

Предложение 3. F: Е —> ?/(s>, определенный как Fx = ||х||, есть RN-функтор.

Определение 3. (S) является максимальным, если не существует S’c S, такого, что (S) с (S') с ?.

Свойства (S) позволяют интерпретировать его как множество доказуемых высказываний теории. Элементы S получают в этом случае имя RN-аксиом и рассматриваются как образующие множества (S), аналогично тому, как аксиомы генерируют доказуемые высказывания (формулы). В роли правильно построенных формул (ппф) фигурирует множество объектов категории Е.

Определение 4. RN-категорная интерпретация релевантной логики представляет собой пару (E,(S)), описывающую множество всех ппф и множество доказуемых следствий.

Будем говорить, что RN-логика (E,(S)) (синтаксически) непротиворечива, если (S) * Е.

RN-логика (E,(S)) (синтаксически) полна, если для любого RNвысказывания р либо pe (S), либо Npe (S), но не одновременно. Это эквивалентно тому факту, что-либо р ~s 1, либо Np ~_s 1.

В случае конечного числа аксиом (которые могут быть сведены к одной, представляющей собой их конъюнкцию) мы имеем S = {р, …, р") и (S) = S, с р = {р, …, р") и справедливы следующих три утверждения:

• (Е, S_p) непротиворечива, если 1 —> р есть стрелка в Е,
• (E, S_P) полна тогда и только тогда, когда р является минимальным в упорядочении, индуцированным в Е нредупорядоченной природой стрелок, и
• (E,(S)) непротиворечива тогда и только тогда, когда (E, S_P) непротиворечива для всех pe (S)

Последний результат можно рассматривать как своеобразный вариант теоремы компактности.

Пусть теперь пара (E,(S)) представляет собой перевод релевантной логики, т. е. (E,(S)) есть RN-логика и пусть Е будет нетривиальной RN-категорией.

Определение 5. В-оценка представляет собой RN-функтор v: E-> В. Элемент реЕ будет истинным по отношению к V, если vpeS^Bi, где S®i = {х: 1 —> х есть стрелка в В}. RN-логика (E,(S)) семантически непротиворечива, если существует оценка V, такая, что ре S влечет уре S^B.

При выполнении этих условий легко доказать, что vpeS^Bi для всех pe (S), а также, что функтор F: Е -> E/_(S), определенный как IMI 1И = Vp, будет RN-функтором.

Определение 6. Моделью (E,(S)) является В-оценка V, такая, что vpeS^В для всехpeS.

Таким образом, суммируя, получаем, что (E,(S)) является семантически непротиворечивой тогда и только тогда, когда (E,(S)) имеет модель.

Теорема 2. (E,(S)) семантически непротиворечива тогда и только тогда, когда (S)) есть собственное множество.

Доказательство. Пусть (?,(S)) будет семантически непротиворечива и пусть v будет ее моделью. Поскольку vl = 1' (по свойству Л/-функтора) и поскольку -.(1 = N) ввиду того, что В нетривиальна, то Nle (S) и, следовательно, (S) является собственным. Наоборот, пусть (S) будет собственным. Доказательство проводим как в [Максимова 1973]. Сконструируем модель (?,(S)). Допустим, что существует S’eE, такое, что (S) с (S'), где (S') будет максимальным (собственным). Определим теперь.

Н = {(D): (S) с (D) ф ?}.

Н непусто, ибо (S)eH. Более того, если (D_a) есть семейство элементов Н, линейно упорядоченное по включению, то тогда 1J (D_a) = (tJ (D")). По лемме Цорна Н имеет максимальный элемент (S), что означает, что-либо pe{S либо Npe (S') для всех (S'). Теперь определяем отображение v: Е —> В условием VpeS^B_u если pe (S), либо vptSr 1, если Npe (S'). Это дает нам RN-функтор, который и является моделью (?,(S)). ?

Определение 7. (E,(S) семантически полна, если выполняется следующее условие: р доказуемо (т.е. />e (S)) тогда и только тогда, когда р истинно во всех моделях (E,(S).

Теорема 3. (?,(S)) семантически полна.

Доказательство. Очевидно, что если pe (S), то vpeS для всех оценок V. Наоборот, пусть peS будет истинным во всех моделях (E,(S)). Определим множество (S)). Если (Su (N/>)) * ?, то RN-логика (E,(Su (Np)) будет непротиворечивой и будет иметь модель V, которая, ввиду (S)c (Su (A//;)), должна также быть моделью (E,(S)). Отсюда получаем противоречие: vNpeS⁽ поскольку W/>e (Su (A/p)) (vNp s NvpeS по свойствам RNи R-функторов соответственно). Поэтому (Su (Np))= Е и отсюда pe (Su (Np)). Тогда существует такое qe (S), что [q.Np] —> р есть стрелка. Но отсюда ввиду q —> [q, Np] получаем стрелку q -> р, следовательно, <7eS_pc (S). ?