Модель № 5 для оценки безошибочности информации после контроля

Требуемая безошибочность информации после контроля обеспечивается за счет использования эффективных средств и способов выявления и исправления ошибок, в том числе по скорости этого процесса и по недопущению ошибок контроля 1-го и 2-го рода, и рациональной регламентации работы контролера.

Моделируемые случаи соотношений между временами, характеризуемыми изначальной частотой допускаемых ошибок в документе, длительностью работы контролера, наработкой до совершения ошибки 1-го и 2-го рода, объемом контролируемой информации и скоростью контроля, отражены на рис. 6.8.

Случаи 1, 2, 3 характеризуют наличие ошибок после контроля, случаи 4, 5 — обеспечение безошибочности после контроля (см. рис. 6.8).

Для описания процессов контроля безошибочности информации приняты обозначения:

V — объем контролируемой информации;

р — доля первоначальных ошибок в проверяемой информации (до контроля);

v — средняя скорость контроля информации;

п — частота ошибок контроля 1 -го рода;

Т’мар — среднее время наработки контролера на ошибку (2-го рода), после истечения которого первая же ошибка в документе оказывается пропущенной, для ПТС контроля это время наработки на отказ;

Tj_K._lip — период непрерывной работы контролера;

Угадан ^— задаваемое допустимое время на процедуру контроля информации.

Рис. 6.8. Иллюстрация формальных процессов контроля безошибочности информации (фрагмент)

Возможны четыре варианта соотношений между временем реального контроля Г_реа;…всего объема документа Г_реальн = V/v, задаваемым допустимым временем контроля Г_задан и непрерывным временем работы контролера Г_непр (рис. 6.9).

Вариант 1. Задаваемое допустимое время контроля не меньше, чем время реального контроля (т.е. Г_реальн< Г_задан), а объем проверяемой информации достаточно мал, что позволяет проверить его за один период непрерывной работы контролера (Г_реальн< Г_непр).

Для экспоненциальной аппроксимации распределений интервалов между ошибками в проверяемой информации, времени до совершения ошибки 1-го рода и времени наработки контролера на ошибку, а также при условии независимости исходных характеристик вероятность Д"осле (1)(У> Ц. V, п, Г_нар,.

Г_непр, Г_задан) отсутствия ошибок в информации после контроля для варианта 1 вычисляют по формуле.

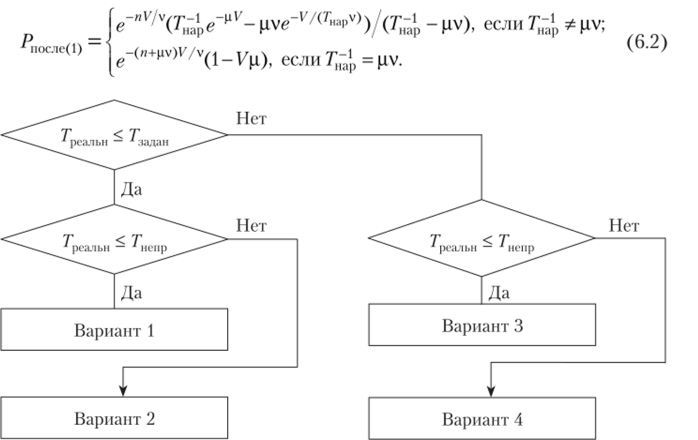
Рис. 6.9. Различные условия контроля безошибочности информации.

Вариант 2. Задаваемое допустимое время контроля не меньше, чем время реального контроля, т. е. Г_реальн < Г_задан, но объем проверяемой информации относительно большой Г_реальн > Г_непр. Это требует нескольких (N) периодов непрерывной работы контролера, в общем случае N= V/ (vr_iienp). Внутри каждого периода проверяют часть всего объема, равную в среднем К_|аСти (2> = У / N, а допустимое время контроля информации для этой части принимают равным Г_задан части (2) = ^задан/ N. Тем самым для каждой проверяемой части информации выполняются условия варианта 1. Вероятность Рпосле (2)(в. V, п, Г_нар, Г_непр, Т_1адаи) отсутствия ошибок в информации полного объема после контроля для варианта 2 вычисляют по формуле.

Вариант 3. Задаваемое допустимое время контроля меньше, чем время реального контроля, Т' _Ь1| > Г_задан, т. е. объективно может быть проверена лишь часть от всего объема информации, равная объему Т_части/₃₎ = уГ_задан В свою очередь, сам объем проверяемой информации относительно мал и может быть проверен за один период непрерывной работы контролера, т. е. Г_реальн < Г_11Спр и для проверяемого объема У_части") выполняются условия варианта 1. Вероятность ^^>_после(3)(^ v, ^п> 7'_иар, 7'_1С[|р, 7_аадан) отсутствия ошибок в информации полного объема после контроля для варианта 3 вычисляют по формуле.

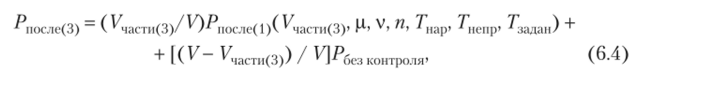
где вероятность отсутствия ошибок в непроверенной части информации V— К_{|асти (3}) равна Р_{Сжз кошроля} = еГ^м0 ?^К|ас™<³>⁾, а вероятность отсутствия ошибок в объеме проверенной информации равна /^>_После (1)(^части (3>" IT ^v> ^п> ^нар" Т Т)

^л непр' •‘задай/*.

Вариант 4. Задаваемое допустимое время контроля меньше, чем время реального контроля, Г_реальп > Г_задан, но объем проверяемой информации относительно большой, Г_реальн > Г"_епр. Аналогично варианту 3 реально может быть проверена лишь часть от всего объема, равная К,_{асти (4)} = vT_3aaail. Относительно этой части возможны два подварианта:

• • подвариант 4.1: Г_задан < Г_иепр, т. е. проверка будет завершена за один период непрерывной работы контролера;
• • подвариант 4.2: Г_задаи> Г_пепр, т. е. потребуется несколько (АО периодов непрерывной работы контролера, в общем случае N = V₄._ACTn^/ (vTj_ICIip).

Для нодварианта 4.1 вероятность P_{n0CJie (4}.)(V> ^ v, п_} Г_пар, Г_непр, Г_задан) отсутствия ошибок в информации после контроля вычисляют по формуле.

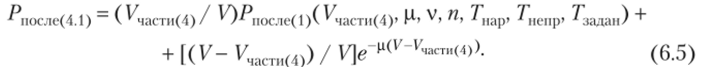
Для нодварианта 4.2 внутри каждого периода проверяют новую часть, равную в среднем К_1асти(₄.₂) = ^_чаСти (4) / М ^и допустимое время контроля ДЛЯ ЭТОЙ НОВОЙ части принимают равным Т_{ЗАдт1 части}(₄2)⁼ ^задан/ N. Вероятность Р_110Сле (4.2))(К I¹' ^v> Я, Т’нэр" ^непр" ^задан) ОТСУТСТВИЯ ОШИБОК В информации мосле контроля вычисляют по формуле.

Таким образом, вероятность отсутствия ошибок в информации после контроля Р_после за заданное время Г_задан определяется аналитическими выражениями для Рц_0Сле(у Рцосле (2у^после (3)>^после (4.1)"^после (4.2) ^R зависимости от варианта соотношений между исходными данными.

Для всех четырех вариантов частота ошибок после контроля р_после =.

— р (1 — Р_после) —

Необходимые для моделирования пределы исходных значений V, Г_задан задают в ТЗ, диапазон возможных значения р, v, п, Г_нар устанавливают в результате натурных экспериментов, дополнительного моделирования или сравнения с аналогами, значение Г_непр указывают в эксплуатационной документации.