Применение функций комплексного переменного в гидродинамике

Рассмотрим установившееся течение жидкости, при котором все частицы движутся параллельно одной и той же плоскости, причем точки, расположенные на одном перпендикуляре к этой плоскости,.

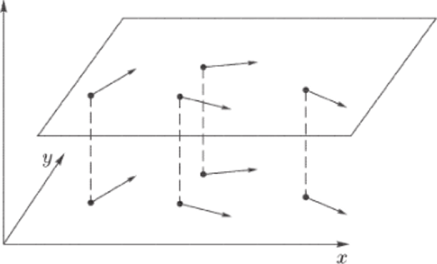
Рис. 29.

имеют равные скорости и направления движения (т.е. векторы скоростей в этих точках равны) — см. рис. 29. Такое течение называется установившимся плоско-параллельным течением. Вектор скорости V не зависит от времени, а зависит только от проекции (#,"/) этой точки на плоскость. Обозначим координаты вектора V через X, Y.

Будем предполагать, что функции X, У имею! непрерывные частные производные первого и второго порядков в некоторой односвязной области D и что поле векторов V удовлетворяет следующим двум условиям.

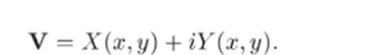
Тогда.

1) Поле V потенциально, т. е.

Это условие означает, что в потоке жидкости отсутствуют вихри (можно сформулировать это свойство и так: интеграл f Xdx + Ydy

г по любому замкнутому контуру Г, лежащему в D, равен нулю). Условие (14.1) равносильно тому, что выражение Xdx + Ydy является полным дифференциалом некоторой функции и = и (х, у), т. е. найдется такая функция и = и (х, t/), что.

• (доказательство этого факта имеется, например, в книге Н. С. Писку нова |7, т. 2. Гл. XIII, § 9|).
• 2) Поле V соленой дал ыю, т. е.

Физический смысл этого условия состоит в том, что в области D отсутствуют источники и стоки, т. е. траектории частиц линии тока не возникают и не обрываются во внутренних точках области D. Равенство (14.3) означает, что выражение —Yds -I- X dy также является полным дифференциалом: найдется функция v = v (x, y), такая что.

Отмстим без доказательства, что функция v (x, y) имеет следующий физический смысл. Возьмем любые две точки (#1,1/1) и (#2? У2) и D и соединим их произвольной гладкой кривой Г С D. Из каждой точки этой кривой восстановим перпендикуляр высотой 1 к плоскости, содержащей Г (т.е. построим «забор» высотой 1, опирающийся на Г). Тогда разность *'(#2.½) — v (x. у) равна объему жидкости, протекающей через построенную поверхность в единицу времени. Эта величина называется потоком жидкости через кривую Г; она зависит лишь от начальной и конечной точек кривой, но не от ее формы.

Рассмотрим линию уровня функции v, т. е. множество точек (#, t/) 6 D, для которых v (x.y) = С, где С — некоторая постоянная. Найдем касательный вектор к этой кривой в произвольной ее точке (#, т/). Уравнение v (x, y) = С можно рассматривать как уравнение Таким образом, тангенс угла наклона касательной равен Y/X. Отсюда следует, что вектор скорости V = {Х, У} направлен по касательной к линии уровня в каждой точке этой линии. Значит, линии v (x, y) = С являются линиями тока. Поэтому функция v называется функцией тока.

Составим теперь функцию комплексного переменного f (z) = и + + it?, где z = х + гу. Эта функция называется комплексным потенциалом поля V. Из равенств (14.2), (14.4) следует, что функция f (z) удовлетворяет условиям (6.4) Коши Римана, а значит, является аналитической в D. Итак, комплексный потенциал установившегося плоско-параллельного потенциального и соленоидального течения жидкости является аналитической функцией.

Так как f (z) аналитична, то ее производная f'(z) не зависит от направления. Дифференцируя равенство }(z) = и + iv по х и используя условие Коши Римана, получим.

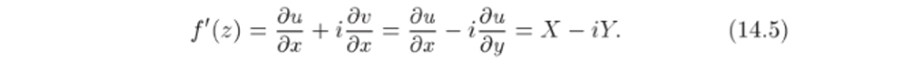
Таким образом, производная комплексного потенциала является вектором, комплексно сопряженным вектору скорости течения.

Покажем, что любую аналитическую в D функцию f (z) = и + iv можно рассматривать как комплексный потенциал векторного по-

ля V = + i потенциального и соленоидального. (В этом и со стоит гидродинамическая интерпретация аналитической функции.).

Обозначим ^ = X. = У. В силу условий Коши-Римана выпол;

дх ду

пены равенства (14.4). Дифференцируя первое из этих равенств по у, второе по х, н вычитая из второго первое, получим (14.3). Проделывая те же операции с равенствами (14.2), получим (14.1). Но условия (14.1), (14.3) и означают потенциальность и соленоидальность по ля V соответственно.

кривой у = у (х), заданной неявно. Дифференцируя обе части, но х, получим.

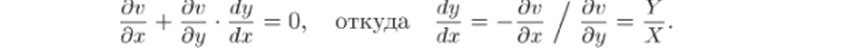
Интерпретация аналитической функции как комплексного потенциала векторного поля позволяет решать ряд важных задач гидродинамики, электростатики и др. Покажем на примере, как решается задача обтекания.

Рассмотрим бесконечно глубокое течение над плоским дном, обтекающее препятствие высотой h — рис. 30, а. В качестве области D здесь будет верхняя полуплоскость с вырезанным отрезком. Для изучения соответствующего векторного ноля найдем его комплексный потенциал. Воспользуемся тем, что линии тока удовлетворяют уравне ниям v (x, у) = С. В плоскости переменного w = и + iv уравнения v = = С определяют горизонтальные прямые. Значит, функция w = f (z) отображает линии тока и горизонтальные прямые, а область D — в область D', образованную семейством горизонтальных прямых. Покажем, что область D' является полуплоскостью Im w > vq (и нс может быть, например, полосой). Зафиксируем Z = 2ih, и пусть zo = iy. При у —> +оо поток жидкости через отрезок [z, Z2] также неограниченно возрастает. Поэтому ?;(0, у) — v (0,2h) -+ 00, а значит, и v (0,у) -4 оо при у -+ оо. Отсюда и следует, что образом области D является полуплоскость Imm > VoРавенства (14.2), (14.4) показывают, что прибавление к f (z) произвольной постоянной также дает комплексный потенциал. Поэтому можно считать, что функция w = f (z) отображает область D на верхнюю полуплоскость. Итак, для отыскания комплексного потенциала f (z) достаточно найти конформное отображение области D на полуплоскость Im ш > 0. Искомое отображение проведем в три этапа.

• 1. Функция W = z² отобразит D на плоскость с вырезанным лучем Re wi ^ —/г². Читатель может убедиться в этом, рассматривая образы каждого из четырех прямолинейных участков границы области D (отрезок [0,г/г] проходится дважды).
• 2. Функция W2 = tv + hr сдвигает полученную область на hr единиц вправо, переводя ее в плоскость с вырезанной положительной полуосью.

3. В полученной области возьмем регулярную ветвь функции го = = /го2' определяемую следующим 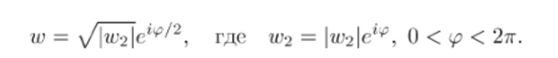образом:

При отображении w = верхний край разреза 0 ^ |гг2| < ос, = О, перейдет в такой же луч плоскости tv, а нижний край 0 ^ |tvo| < 00, <�р = 27 Г — в отрицательную полуось 0 ^ w < 00, arg tv = тг. Поэтому плоскость с разрезом по положительной полуоси перейдет в верхнюю полуплоскость.

Композиция указанных трех функций и даст нужное отображение:

Рис. 30.

Это отображение не единственное: функция к у/z² + h², к > 0. также переводит D в верхнюю полуплоскость. Постоянную к можно найти, если задать скорость потока на бесконечно большом удалении от препятствия. Действительно, из равенства (14.5) следует, что f'(z) = = |V|. Поэтому.

Устремляя 2 к оо, получим |/^/(оо)| = к = V^c • Отсюда.

и комплексный потенциал найден. С его помощью можно получить важнейшие характеристики потока: величину и направление векторов скоростей частиц, уравнение линий тока, расход жидкости и т. д. Например, из (14.6) следует, что у основания препятствия (z = 0) скорость равна нулю (застойная зона), а в точке г = ih — бесконечности (эффект острия).

Найдем уравнения линий тока. Эти линии определяются равенствами v (x, у) = С. Поэтому нужно либо отделить мнимую часть у функции f (z) =u + iv, определяемой формулой (14.7), либо рассмотреть (14.7) как систему уравнений с переменными и, х, у и исключить и. Рассмотрим второй способ. Из (14.7) получаем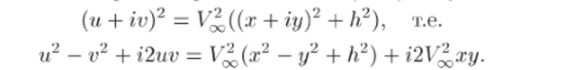

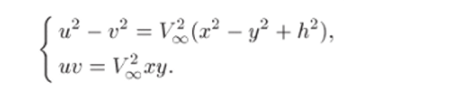
Приравнивая действительные и мнимые части, приходим к системе уравнений Исключим отсюда переменное и, выражая его из второго уравнения и подставляя в первое. Обозначим для удобства с = v/V^. Поскольку v = С — фиксированная величина, то с — тоже постоянная. После элементарных преобразований придем к равенству.

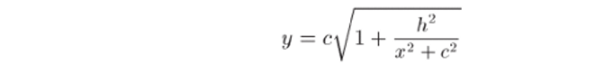
(соответствующие линии тока изображены на рис. 30, а).

Комплексный потенциал можно строить и для векторных полей в многосвязных областях. Функция /(г) оказывается при этом, вообще говоря, многозначной. Мы не останавливаемся далее на этих задачах, рекомендуя читателю книги [1]. [5], [9]. [13], в которых рассматриваются многочисленные применения функций комплексного переменного в гидродинамике, электростатике и др.

Упражнение. Рассмотрите задачу обтекания препятствия в виде полукруга (рис. 28, б).