Анализ точности результатов выборочного исследования на основе доверительного интервала

Довольно распространенным является мнение о том, что увеличение точности результатов выборочного исследования пропорционально увеличению числа элементов выборки. Это мнение не совсем справедливо. Более 90% ошибок измерений имеют «невыборочные» источники, и лишь 10% ошибок появляются в результате неправильного формирования выборки [261. Мнение об обязательном повышении точности с ростом численности выборки основывается на ряде заблуждений, к сожалению, разделяемых многими исследователями.

Пример 7.12. Заблуждение: чем больше выборка, тем она репрезентативнее. То, что это не всегда так, демонстрирует уже упомянутый выше пример с прогнозированием исхода президентских выборов в США в 1936 г.: выборка объемом свыше 2 млн респондентов не обеспечила репрезентативности, прогноз оказался неверен. Выборка, состоящая из 100 элементов, может обеспечить лучшую репрезентативность, чем выборка, состоящая из 10 000 элементов.

Пример 7.13. Заблуждение: выборка должна состоять из как минимум 10% элементов генеральной совокупности. На самом деле абсолютный объем выборки — фактор гораздо более важный, чем объем выборки относительно объема генеральной совокупности. Так, например, выборка объемом 100 элементов, извлеченная из 1000 элементов генеральной совокупности, может обеспечить примерно такую же точность оценки, как выборка объемом 1000 элементов, отобранных из 100 млн элементов, формирующих генеральную совокупность. Например, при опросах общественного мнения о возможном исходе выборов президента США обычно формируется выборка, насчитывающая всего 1500— 2000 респондентов, тогда как весь электорат США насчитывает около 150 млн чел. Однако при формировании выборки из большой популяции возникает проблема отбора соответствующих элементов.

Пример 7.14. Заблуждение: заранее невозможно ответить на вопрос о необходимой и достаточной численности выборки. Эго отчасти так. Действительно, требуемый объем выборки можно определить после того, как проведен анализ хотя бы нескольких случайным образом предварительно отобранных элементов генеральной совокупности. Но это может (и должно) быть сделано на стадии предварительного тестирования, что является обязательным этапом любого серьезного исследования. Кроме того, сделать заключение о необходимом объеме выборки можно по результатам предыдущих исследований.

Необходимый объем выборки представляет собой функцию вариации измеряемых параметров генеральной совокупности и точности оценки этих параметров, требуемой исследователем. Например, в зависимости от требуемой точности для одной и той же совокупности может быть достаточно 50,.

500 или 5000 элементов выборки. И напротив, заданную точность могут обеспечить 100, 1000 или 10 000 элементов в зависимости от того, насколько велика дисперсия полученных измерений.

Общим правилом при формировании выборки является следующее: чем больше дисперсия оцениваемых параметров генеральной совокупности, тем больший объем выборки нужен для того, чтобы обеспечить требуемую точность. Например, если мы выясняем мнение по определенной теме, когда все представители популяции (элементы генеральной совокупности) имеют предположительно одинаковое мнение, нам достаточно опросить одного представителя. Если возможны два мнения, нам необходима выборка из по меньшей мере двух элементов (но при этом мы должны позаботиться о том, чтобы в выборку попали носители этих различных мнений, и нам понадобится большая выборка, чтобы определить частотность встречаемости этих мнений). Если возможны 10 точек зрения, нужна еще большая выборка, и т. д.

С практической точки зрения главными факторами, определяющими объем выборки, являются желаемая точность оценки и бюджет исследования. По поводу бюджета особые комментарии не требуются. Если, скажем, в бюджете исследователя имеется 1000 руб., а телефонный опрос каждого респондента требует в среднем 10 руб., то максимальный объем выборки — 100 элементов. Если нужна выборка большего объема, то необходимо выбирать другие, более дешевые формы опроса. Более интересным в контексте тематики данной главы является вопрос об объеме выборки с позиций точности оценки измеряемых параметров.

Оценка параметра может быть точечной или интервальной. Примером точечной оценки является результат гипотетического выборочного исследования, установившего, что 61% опрошенных пользователей телефона определенной торговой марки остались довольны сделанной покупкой, или 73% граждан, участвовавших в опросе общественного мнения, поддерживают новые инициативы правительства [5, 6]. Как мы уже говорили, результаты выборочного исследования нельзя напрямую переносить на генеральную совокупность, т.с. мы не можем сказать, что именно 61% всех пользователей данной марки телефонов ими довольны, или что точно 73% всех граждан страны поддерживают новый закон. Очевидно, что здесь должен быть некоторый допуск, или интервал, в пределах которого можно формулировать результат, например: от 45 до 75% пользователей телефона остались довольны сделанной покупкой и т. п. Последний подход, безусловно, более оправдан при выборочном исследовании.

Точность интервальной оценки параметра, измеряемого при выборочном исследовании, определяется двумя показателями:

• а) интервалом, в котором ожидается обнаружить оцениваемый параметр;
• б) вероятностью обнаружения этого параметра в данном интервале.

Эти два показателя объединяет понятие доверительного интервала.

Процедура определения доверительного интервала основана на центральной предельной теореме — одной из основных теорем теории вероятностей и статистики. Согласно этой теореме распределение средних значений выборок, извлекаемых из одной и той же совокупности, соответствует нормальному распределению. Более того, когда выборки становятся достаточно большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной. Среднее значение всех выборочных средних равно среднему значению генеральной совокупности (р), а стандартное отклонение выборочных средних (ct_v) определяется по формуле.

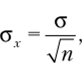
где п — объем выборки; а — стандартное отклонение (или среднее квадратичное отклонение) по генеральной совокупности (корень квадратный из дисперсии):

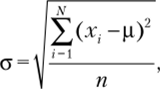
N — объем генеральной совокупности.

Величина cr_v называется также стандартной ошибкой среднего {standard error of the mean), иногда используется термин «средняя ошибка выборки». Вычисление стандартной ошибки среднего основывается на предположении о нормальности измеряемой переменной. Если это предположение не выполнено, то оценка может оказаться неверной, особенно для малых выборок.

Естественным образом возникает вопрос о том, какой объем выборки может считаться достаточно большим. Известно эмпирическое правило, согласно которому принимается, что если объем выборки (п) равен 100 или более, то применима центральная предельная теорема и допущение о нормальности распределения всех возможных выборочных средних может быть принято. Показано, что при увеличении объема выборки до 100 и более качество оценки стандартной ошибки среднего улучшается и без предположения нормальности выборки. Если же п меньше 100, то нужно иметь доказательства нормальности распределения генеральной совокупности, и только в этом случае можно полагать, что распределение, которому подчиняются выборочные статистики, является нормальным. Если таких доказательств нет, необходимо проверять нормальность выборочного распределения.

Поскольку в большинстве случаев значение стандартного отклонения по генеральной совокупности (а) неизвестно, его заменяют выборочным стандартным отклонением (5). Выборочное стандартное отклонение (стандартное отклонение по выборке) определяется как.

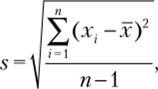
где х — среднее значение изучаемого признака по выборочным наблюдениям. В математической статистике доказано, что стандартные отклонения по генеральной и выборочной совокупностям связаны соотношением.

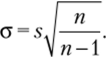
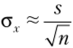
(предполагается, что выборка формируется в результате случайного повторного отбора). Отсюда следует, что стандартное отклонение по выборке определяет интервал попадания среднего по всей генеральной совокупности. Стандартная ошибка среднего зависит от стандартного отклонения, но выборке и ее объема. Например, если стандартное отклонение по выборке s = 0,74 и п = 10, то стандартное отклонение выборочных средних равно.

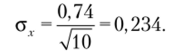
Если стандартное отклонение по выборке уменьшается в два раза, то оцениваемое изменение измеряемого параметра по генеральной совокупности также уменьшается в два раза:

Предположим, что по результатам выборочного исследования мы получаем стандартную ошибку среднего.

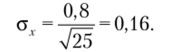
При увеличении количества респондентов в четыре раза при том же самом значении стандартного отклонения по выборке мы можем обеспечить увеличение точности лишь в два раза:

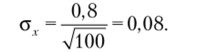
При бесиовторном случайном отборе численность генеральной совокупности в ходе формирования выборки сокращается. Поэтому при такой схеме формирования выборки стандартное отклонение выборочных средних рассчитывается как.

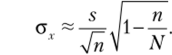
Очевидно, что для применения этой формулы (и этого механизма отбора соответственно) нам должна быть известна численность генеральной совокупности N.

Для нормального распределения существует универсальное соотношение между относительной частотой встречаемости в генеральной совокупности значений х, средним значением (р) и стандартным отклонением (а). Это соотношение называется законом нормального распределения:

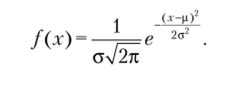
Это соотношение удобно представить для стандартного нормального распределения (или z-распределения) в виде.

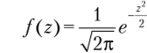
Стандартное нормальное распределение имеет среднее значение, равное нулю, и стандартное отклонение, равное единице. Поэтому для обозначения стандартного нормального распределения также используется термин единичное нормальное распределение.

Любое нормальное распределение может быть сведено к 2-распределению с помощью простого преобразования:

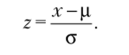
Последняя формула называется стандартным z-преобразованием, переводящим измерения в стандартную z-шкалу. В результате такого преобразования значения z выражаются в единицах стандартного отклонения от среднего.

Отсюда следует, для любого 2 можно однозначно определить площадь под кривой любого нормального распределения вне зависимости от величины среднего значения и стандартного отклонения. Так, например, для z = 1 около 68,27% всех значений признака располагаются в пределах одного стандартного отклонения по обе стороны от среднего значения при любом нормальном распределении (рис. 7.2). В пределах трех стандартных отклонений (г = 3) умещается почти вся генеральная совокупность, а именно 99,73%.

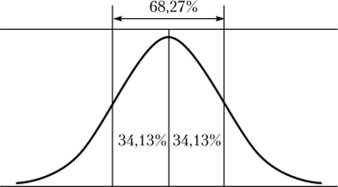
Рис. 7.2. Площадь под кривой нормального распределения (г = 1).

Важным практическим следствием этого свойства является возможность оценить точность определения изучаемого параметра на основе выборочного исследования. Так, с вероятностью Р = 0,6827 значение изучаемого параметра по генеральной совокупности, который оценивается, но элементам выборки, будет попадать в интервал х ± а_х.

Для 2 = 2 значение вероятности составит 0,9544, т. е. в 95,44% случаев значение исследуемого параметра будет попадать в интервал х ± 2а_г Для 2=3 значение вероятности составит 0,9973, т. е. в 99,73% случаев значение параметра будет лежать в интервале х ± Зст_г

Значения z для других значений вероятности можно определить из таблицы в приложении П4 или с помощью функции MS Excel НОРМСТОБР, возвращающей значение 2 при заданной вероятности.

Если известны среднее арифметическое значение по выборке (х) и выборочное стандартное отклонение (s), легко определить стандартную ошибку среднего а_х. Используя соответствующую статистическую таблицу и задавая необходимое значения вероятности (требуемый уровень статистической значимости р = 1 — Р), можно определить значение z, которое соответствует заданному значению вероятности попадания среднего значения параметра по генеральной совокупности в интервал, А = х ± za_x.

Величина, А называется доверительным интервалом (confidence interval), а величина 5 = ±zg_v — предельной ошибкой среднего (или предельной ошибкой выборки). Доверительный интервал фактически характеризует точность оценки измеряемой величины. Таким образом, для оценки точности выборочных измерений достаточно определить среднее значение и стандартное отклонение по выборке, а также задать уровень значимости.

Очевидно, что с увеличением значения z возрастает вероятность попадания среднего в доверительный интервал А, но при этом диапазон оценки становится неопределеннее и размытее, что уменьшает точность оценки (чем менее определенным является прогноз, тем с большей вероятностью он осуществится). Поэтому не следует стремиться задавать очень большое значение вероятности. Вполне достаточным является 90%-ный или 95%-ный уровень значимости (р < 0,05). Поскольку стандартное отклонение средних значительно меньше стандартного отклонения индивидуальных откликов, приемлемым считается даже 68%-ный доверительный интервал [6].

В случае когда выборка состоит менее чем из 100 элементов или когда нет достаточных оснований считать выборочное распределение нормальным, для определения доверительного интервала рекомендуется использовать другое теоретическое распределение —^{-распределение} Стьюдента. В этом случае процедура определения доверительного интервала аналогична случаю больших выборок, но вместо значения z используется значение^{-критерия} Стьюдента. Это значение зависит от объема выборки и задаваемого уровня вероятности. Значение^{-критерия} можно определить из таблицы в приложении П4 или с помощью функции MS Excel СТЬЮДРАСПОБР (1 — Рп- 1).

Пример 7.15. Для иллюстрации метода определения доверительного интервала рассмотрим следующий пример. Группа студентов университета разрабатывает проект по созданию университетского ланч-клуба (гибрида студенческой столовой и фешенебельного ресторана). Поскольку студенты помимо фонтана творческих идей и безудержного энтузиазма имеют еще и достаточно здравого смысла, подкрепленного знаниями основ математики, они решают провести мониторинг ряда параметров, на основании чего и принять решение об организации работы предполагаемого заведения. Пусть в качестве измеряемого параметра выступает «предпочтительное время обеда». Проведено предварительное выборочное измерение (объем выборки — 10 элементов, выборки формировались в результате случайного повторного отбора). Респондентам предлагалось выбрать время начала обеда из пяти предложенных вариантов: 11:00, 11:30,12:00,12:30,13:00. Отклики респондентов кодировались как 1,2,3,4,5, соответственно выбранному времени. Поскольку интервалы между позициями выбранной шкалы равны и соответствуют 30 мин, используемую шкалу можно рассматривать как интервальную. Результаты предварительного выборочного исследования представлены в таблице.

Определяя стандартную ошибку среднего по характеристикам выборки, получим.

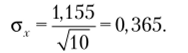
Значение стандартного отклонения переводится во временной диапазон исходя из дизайна анкеты: интервал в 1 пункт соответствует 30 мин. Поэтому значение 0,5 соответствует 0,5 • 30 = 15 мин, а 0,365 соответствует 0,365 • 30 = 11 мин. Таким образом, по результатам выборочного исследования мы можем оценить интервал изменения среднего по генеральной совокупности. Для z = 1 он составляет 3,0 ± 0,365, т. е. 12:00 ±11 мин (рис. 7.3).

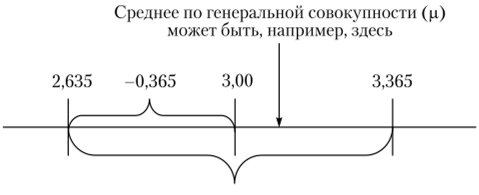
Рис. 7.3. Доверительный интервал к примеру 7.14.

При этом вероятность попадания среднего, но генеральной совокупности в этот интервал равна приблизительно 0,68, так как мы принимаем 2=1. Аналогично с вероятностью 0,95 по характеристикам выборки можно утверждать, что интервал изменения среднего по генеральной совокупности Д = 3,0 ± 0,365 -1,96 = = 3,0 ±0,715 (12:00 ±21,5 мин).

Однако, как отмечалось ранее, такой подход к определению доверительного интервала нс совсем корректен, так как объем выборки мал (п < 100). Поэтому в данном случае необходимо использовать значение f-критерия. Для п = 10 и Р = = 0,95 (95%)t= 2,262 (см. приложение I14). Соответственно, А =3,0 ± 0,365−2,262 = = 3,0 ± 0,826 (12:00 ±25 мин).

В ряде случаев подобные задачи необходимо решать по сгруппированным данным, когда указывается, сколько раз в выборке встречается определенное значение изучаемого признака. В таком случае среднее значение признака рассчитывается не как среднее арифметическое (сумма значений признака по элементам выборки, деленная на количество элементов), а как среднее арифметическое взвешенное. В научной и учебной литературе по математической статистике представлены разные подходы к определению среднего (в том числе среднего арифметического, среднего арифметического взвешенного, среднего гармонического, среднего геометрического и др.)^[1].

Число одинаковых значений признака в ряду распределения называется частотой и обычно обозначается /.

Среднее арифметическое взвешенное определяется как.

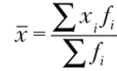
а стандартное отклонение взвешенное — как.

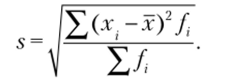
Для определения необходимого количества элементов в выборке нужно задать желаемую точность, характеризуемую предельной ошибкой среднего (а_Л). Поскольку этот параметр связан с объемом выборки, мы можем оценить необходимое количество элементов в выборке исходя из требуемой точности оценки исследуемого параметра генеральной совокупности.

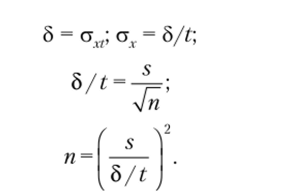
Для иллюстрации будем использовать пример 7.15. Предположим, что необходимо обеспечить точность оценки исследуемого параметра (предпочтительное время обеда) ±15 мин с вероятностью 0,95. Тогда мы задаем предельную ошибку среднего 8 = ±0,5 (±15 мин) и соответственно t = 2,26 (так как п = 10). Далее определяем минимально необходимый размер выборки:

По данным, полученным в результате выборочного исследования, находим.

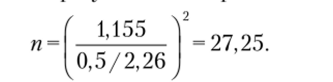
Таким образом, объем выборки должен быть не менее 28 человек, для того чтобы обеспечить точность оценки ±15 мин с вероятностью 0,95. Если необходимо увеличить точность, например до ±10 мин с той же вероятностью, получим большее значение п (в качестве упражнения читателю предлагается самостоятельно решить эту задачу).

Если предварительное тестирование не проводится, но из предыдущих исследований известна величина стандартного отклонения или дисперсии значений изучаемого признака, однако при этом не приводится объем выборки, по которому эта величина получена, значение минимального объема выборки для обеспечения необходимой точности можно получить следующим образом.

Вначале выбирается значение 2-критерия для заданной вероятности Р (или, что-то же самое, для уровня статистической значимости р = 1 — Р), затем определяется первоначальное значение объема выборки (п_{) по формуле.

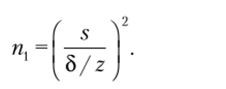
Если найденное значение меньше 100, то вместо 2-критерия используется^{-критерий} (определяемый для найденного значения /?, и заданного/;), и минимальный объем выборки уточняется:

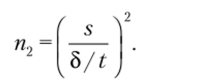
Если при этом п₂ значительно больше п_х и при этом п₂ < 100, можно провести еще одну итерацию уточнения минимального объема выборки с помощью^{-критерия,} который определяется для п₂ и р_} и т. д.

Часто выборочное исследование используется для определения параметров, представляющих собой пропорции от генеральной совокупности. Для иллюстрации вновь вернемся к примеру со студенческим проектом ланчклуба (см. пример 7.15). Предположим, инициаторы этого проекта задались вопросом: «Какой процент студентов университета будет посещать ланчклуб?».

Стандартная ошибка определения пропорции при повторном отборе определяется как.

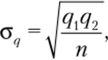
где q_{ — доля элементов генеральной совокупности, обладающих измеряемым атрибутом; q₂ — доля элементов генеральной совокупности, не обладающих измеряемым атрибутом, q₂ = 1 — q_v

Сравнивая эту формулу с формулами для определения ошибки среднего, рассмотренными ранее, легко увидеть, что произведение q_{q₂ имеет смысл дисперсии по выборке. Поэтому в литературе это произведение часто называется групповой дисперсией.

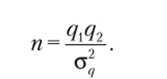
Отсюда получаем Предположим, что предварительное тестирование выявило, что 30% студентов выказали желание посещать клуб (д, = 0,3), но точное значение респондентов, принимавших участие в опросе, неизвестно. Установленная точность оценки: 8 = ±0,1 (10%), 2 = 1,96 (95%). Тогда o_q= 0,1/1,96 = 0,051 и п = 81. Дальнейшее уточнение этого значения с использованием ?-критерия дает п = 83.

В случае если предварительное тестирование не проводится, можно руководствоваться следующей логикой: произведение q$₂ никогда не превы;

0,25.

сит 0,25, поэтому размер выборки можно оценить как п = —.

• [1] См., например, работу [6].