Характеристическая функция случайного процесса

Как отмечалось ранее, при негауссовском случайном процессе отыскание закона распределения на выходе нелинейной цепи является чрезвычайно сложной задачей, зачастую не имеющей прямого решения. Существуют лишь приближенные методы решения, связанные с большими вычислительными проблемами.

Один из таких методов основан на использовании характеристических функций случайного процесса и известных соотношений между характеристической функцией и моментами распределения процесса. Так, в частности, в теории передачи информации часто требуется определить вероятностные характеристики информационных случайных сигналов, преобразованных нелинейными или параметрическими цепями и устройствами (например, в процессе нелинейного усиления, при модуляции, детектировании и т. д.). В этих случаях весьма эффективно применение теории характеристических функций. Пусть имеется случайный процесс X{t), описываемый одномерной плотностью вероятности р (х). Составляющие .r,(/), x₂(t),…, x_k(t),…, x"(t) этой функции, отражающие весь ансамбль реализаций случайного процес;

са, являются отдельными преобразуемыми стохастическими колебаниями, составляющими групповой сигнал.

В теории вероятностей для таких случайных процессов большую роль играет статистическое среднее вида.

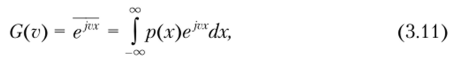
представляющее собой, но существу обратное преобразование Фурье (без коэффициента 1/(2л)) от плотности распределения вероятности р{х) и называемое характеристической функцией случайной величины X. В этом случае функция G (v) является прямым преобразованием Фурье от плотности вероятности (с коэффициентом 1/(2л)), поэтому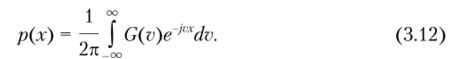

Итак, плотность вероятности р (х) случайной величины может рассматриваться как частотный спектр характеристической функции G (v), а последняя, в свою очередь, — как координатное представление ее закона распределения.

Из математики известно, что можно провести асимптотическое разложение характеристических функций для произвольного распределения. В качестве примера определим характеристическую функцию гауссовского случайного процесса с заданным математическим ожиданием т и СКО о:

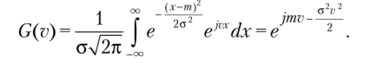oV.

Для центрированного гауссовского процесса (т = 0) имеем G (v) = e ² . Для случайной величины, равномерно распределенной на отрезке 0 < ж < а,

pi™

G (v) = —. jav

Через операцию определения характеристической функции упрощается вычисление моментов случайной величины любого порядка. Такое удобство использования характеристической функции при анализе случайных процессов и вычислении их параметров следует из свойств преобразования Фурье. В частности, характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Если известна характеристическая функция, то легко найти числовые характеристики случайного процесса.

Действительно, поскольку из формулы (3.11) получаем после дифференцирования по степени п

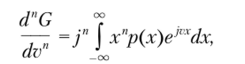
то, полагая г> = 0 и сравнивая результат с моментом п-го порядка случайной величины (3.4), находим.

Начальные моменты случайного процесса можно определить через производные характеристической функции при v = 0. Раскладывая характеристическую функцию случайного процесса в ряд Тейлора, запишем.

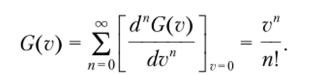
С учетом равенства (3.13) получим.

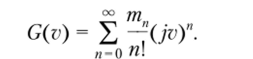
Следовательно, характеристическая функция случайного процесса определяется его моментами распределения. Учитывая связь характеристической функции и плотности вероятности распределения, можно сказать, что моменты распределения вероятности определяют и плотность вероятности случайного процесса.

С помощью характеристической функции удобно также находить плотность вероятности случайной величины, подвергнутой функциональному преобразованию, например нелинейному усилению, модуляции и т. д. Так, при и =f (x)

Теперь, если осуществимо прямое преобразование Фурье (3.12), то поставленная задача вычисления спектра выходного сигнала будет решена.

Пример 3.2.

Пусть задан случайный сигнал и = U_ncosx, у которого амплитуда U₀ = const, а фазах — значение случайной величины, равномерно распределенной на отрезке -п < х < л. С помощью характеристической функции вычислим плотность вероятности распределения амплитуд случайного сигнала.

Решение

Поскольку плотность вероятности распределения фазы случайного сигнала определяется как р_г(^х) ⁼ 1/(2л), то из формулы (3.11) находим характеристическую функцию.

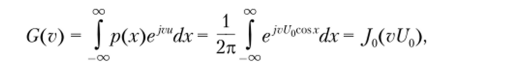
гдеJ_n — функция Бесселя первого рода нулевого порядка.

Применяя табличный интеграл и воспользовавшись последней формулой, получаем для функции плотности распределения амплитуд случайного сигнала.

Такой вид графика распределения плотности вероятности случайного процесса со случайной начальной фазой (рис. 3.11) связан с тем, что если выполнить большую серию испытаний, каждый раз случайным образом выбирая значения фазы х из заданной ее области, то сигнальная функция U₀cosx чаще будет принимать мгновенные значения, близкие к амплитудам ±U₀.

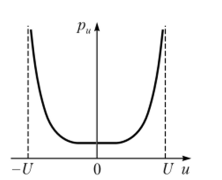
Рис. '3.11. График плотности вероятности распределения амплитуд сигнала со случайной начальной фазой.