Идеи Колмогорова о вероятности

Следует заметить, что до того, как создать систему аксиом в теории вероятностей, А. Н. Колмогоров обсуждал (|99|, 1929) некоторые примеры 'обобщенных вероятностей', которые не могут быть описаны его аксиоматикой. Вероятно нам не нужно называть эти объекты ‘обобщенными вероятностями'. Кажется естественнее называть обыкновенные вероятности (описываемые аксиоматикой Колмогорова) ‘специальными вероятностями'.

Существует и другая сторона общего использования колмогоровского подхода, которая не гак видна, как исчезновение конкретных вероятностных пространств. Эта идея о том, что только измеримые, но Лебегу множества могут играть какую-либо роль в вероятностных рассуждениях. Конечно, это следствие того факта, что Колмогоров обсуждал только продолжение по Лебегу [99] (или продолжение по Борелю [74]). Однако, в принципе, можества неизмеримые по Лебегу могут появиться в вероятностных моделях связанных с какими-либо естественными явлениями. Мы будем обсуждать такую модель в главе 2. С другой стороны, Колмогоров обсуждал в работе |99| нелебеговское продолжение меры Лебега // на отрезке [0,1], а именно, результат Банаха о том, что мера ft может быть продолжена до меры /7, определенной на а-алгебре F[₀.i] всех подмножеств отрезка [0,1]. Заметим, что Колмогоров рассматривал эту меру в качестве хорошего кандидата на вероятность. Он также рассмотрел многомерный случай и обратил внимание на то, что продолжение J1 на алгебру F[₀.i]" лебеговской меры р на кубе [0, l]^ri можно получить используя изометрию куба [0,1 ]", п = 2,3,…, и отрезка [0,1]. Затем он отметил, что в случае п > 2 такая мера не удовлетворяет принципу равенства мер конгруэнтных множеств. Это следствие примера о разложении сферы на три конгруэнтных множества, каждое из которых конгруэнтно объединению двух остальных, и счётного множества (доказательство см., например, в работе |48|):

Теорема 5.1. Сферу S можно разбить на непересекающиеся множества S = A U В U С U Q такие, что: (i) множества А, В. С конгруэнтны друг другу; (и) множество В U С конгруэнтно каждому из множеств А, В, С: (Hi) Q — счётно.

Продолжим изучать вопрос об области определения вероятности. Как мы увидели, из ансамбль-подхода автоматически не следует, что система множеств (событий) F (tts) (соответствующая свойствам тгs ансамбля S)

должна быть алгеброй. С другой стороны, если используется аксиоматика Колмогорова, тогда мы должны начинать (но крайней мере) с алгебры. Однако, могут существовать случайные явления, которые не обладают структурой алгебры. Почему объединение АиВ двух событий А, В обязательно должно быть событием? Почему дополнение D = QC события С всегда должно быть событием? Интересно, что перед тем как предложить общую аксиоматику теории вероятностей (см. [74| 1933), Колмогоров обсуждал задачу области определения вероятности [90) (1929). И в го время он имел точку зрения, которая совпадает с нашей: «Неясно также, когда мера, связанная с какой-либо задачей в вероятностном исчислении, должна быть замкнутой» (т.с. определенной на алгебре). В работе [99) Колмогоров указывал, что «не должно предполагаться то, что из существования мер двух пересекающихся множеств следует существование меры их суммы или разности: несомненно существуют важные меры и без этот свойства». В частности, он обсуждал следующий пример.

Пример 5.1. (Плотность натуральных чисел; подробнее см., например, работы [45], [91]). Для подмножества Л С N величину.

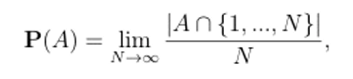
называют плотностью множества А если предел существует. Пусть Q< обозначает класс всех таких подмножеств множества N у которых существует плотность. Ясно, что каждое конечное множество Л с N принадлежит классу G и Р (Л) = 0. Также очевидно, что любое подмножество В = N А, где, А принадлежит Qd и Р (В) = 1 (в частности, P (N) = 1). Читатель легко найдет примеры множеств, А € Qd таких, что 0 < Р (А) < 1.

Предложение 5.1. Пусть А[, А₂ € Qd и А П А₂ = 0- Тогда А U А₂ Е Qd и

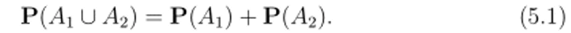
Доказательство. Так как А Г) А₂ = 0, то U А₂) П {1,…, ЛГ}| = l^i П {1,N}| 4−1А₂ П {1,…, N}. ?

Предложение 5.2. Пусть А, А₂ Е QdСледующие условия эквивалентны: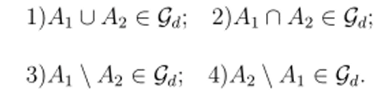

Имеют место стандартные формулы:

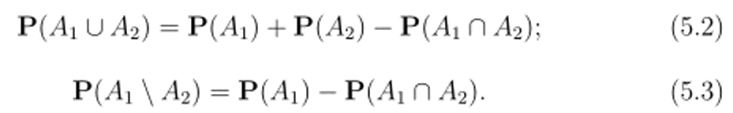
Доказательство. Имеем.

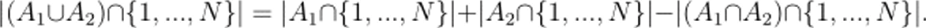
Таким образом, если, к примеру, А П Л₂ € Qd то существует предел правой части равенства. Из чего следует, что Л] U Л₂ G Qd и справедливость равенства (5.2). Остальные импликации доказываются аналогично.? Можно найти множества Л. В 6 Qd такие что, предположим, Л П В # Qd. Пусть Л множество чётных чисел. Возьмём произвольное подмножество С С Л не имеющее плотности. По сути, вы можете найти С такое, что.

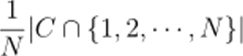
осциллирует. Возникают два случая: СП {2п} = {2п} или = 0. Положим.

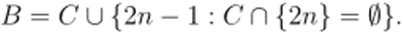
Тогда, и Л и В имеют плотности ½. Но АПВ = С не имеет плотности. Таким образом, Qd не является алгеброй множеств.

В 1929 году А. Н. Колмогоров писал в работе |99|: ¹⁴Неизвестно всякая ли мера замыкаема. Если замыкание и возможно, то не обязательно только одним способом. Может оказаться, что очень трудно найти меру, которая замыкает меру, определённую плотностью натуральных чисел". Мы можем доказать, что плотность натуральных чисел можно замкнуть (продолжить на алгебру всех подмножеств множества N), см. теорему 5.4.

Чтобы формализовать наши рассуждения о плотности натуральных числел, предлагаем следующее определение.

Определение 5.1. Система, подмножеств Q мпоо/сества Q, которая обладает свойствами, описанными в предложении 5.2 и содержит 0 и П. называется полуалгеброй множеств.

Определение 5.2. Функцию Р: Q —" [0,1], где Q полуалгебра, назовём вероятностной полумерой если она удовлетворяет условию аддитивности (5.1) и Р (П) = 1.

Определение 5.3. Тройка V = (Q.Q.P), где Р — вероятностная полумера па полуалгебре Q. назовём полу вероятностным пространством.

К сожалению, мы не сможем сказать ничего больше о таком обобщении вероятностного пространства, поскольку теория интегрирования, но вероятностным полумерам нс развита.

Мы представляем простейшую конструкцию продолжения меры р на алгебру всех подмножеств. Эта конструкция основана на представлении меры р непрерывным линейным функционалом на некотором пространстве функций и применении теоремы Хана-Банаха. Читатель, интересы которого далеки от функционального анализа, может опустить последующие доказательства и ограничиться формулировками.

Теорема 5.2. Пусть р — конечно-аддитивная мера на некоторой алгебре F подмножеств множества П. Тогда существует конечно-аддитивное продолжение Ji меры р на алгебру Fq — всех подмножеств множества П.

Доказательство. Введем пространство ограниченных функций Это нормированное пространство. Полагаем.

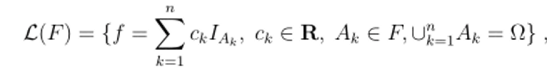
где 1а — характеристическая функция множества А. Оно является нормированным подпространством пространства В (О,). Определим линейный функционал: C (F) —> R по формуле.

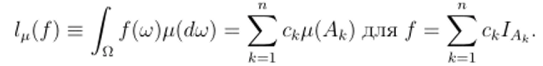
Этот функционал корректно определен (т.е., нс зависит от способа представления функции /). Если.

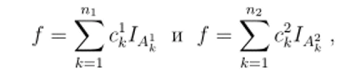
тогда всегда возможно найти множества Д € F (I = 1,…, JV), Д Г) В_т = 0,/ Ф /л, Q = UiLBh такие, что все множества A^J_k, j = 1,2, представляются как объединения множеств Д (конечно, здесь мы используем.

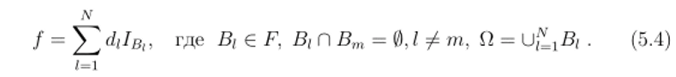
Пользуясь конечной аддитивностью меры р, получаем, что.

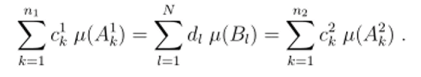
Этот функционал является непрерывным (ограниченным) на нормированном пространстве C (F), и на основе представления (5.4) мы получим:

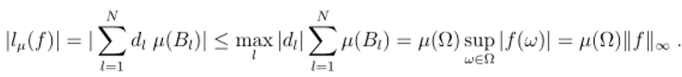
Фактически, норма ||/_;i|| = sup{|/,(/)|: ll/lloo < 1, / € ?(F)} функционала l_fl равняется р (П).

Теперь применяем следующую хорошо известную теорему функционального анализа.

Теорема 5.3. (Хан-Банах) Пусть Е линейное нормированное пространство и пусть U его линейное подпространство. Любой линейный непрерывный функционал /:?/—> R можно продолжить до линейного непрерывного функционала L: Е R так, чтобы нормы функционалов I и L совпадали: ||L,|| = l_fl.

Продолжение на алгебру Fq меры // определим формулой Ji (A) = Т_/д(/д), A G Fq, где L₍,: В (О.) —> R есть продолжение линейного непрерывного функционала l_fl: C (F) —> R, полученное с помощью теоремы Хана-Банаха. Из линейности L_fl следует, что мера Ji конечно-аддитивна.

Наконец, мы должны показать, что Ji (A) > 0 дчя любого А € Fq. Предположим, что существует А е Fq такое, что с = Ji (A) < 0. Тогда р (А) = p (Q)-c > //(П). С другой стороны, Ji (A) = L_tXh) < Рл11оо||.М = Ц/JI = д (П). Эго противоречие и доказывает неотрицательность меры Ji. ?

С другой стороны, Ji может быть не <�т-аддитивна даже если мера // (7-аддитивна. Видимо, ответ на вопрос :

" Возможно ли в общем случае построить а-аддитивное продолжение Ji на алгебру Fq а-аддитивной же меры /г?" неизвестен.

Иная трудность состоит в том, что доказательство теоремы ХанаБанаха основано на аксиоме выбора. Тем самым, мы тоже должны использовать эту аксиому, чтобы получить продолжение вероятности. Однако, место аксиомы выбора в квантовой физике не ясно. Таким образом, не так легко найти область возможных приложений вероятностей, продолженных на алгебру Fq с помощью теоремы Хана-Банаха.

Кажется, что, в общем случае невозможно доказать существование продолжения Ji меры р без аксиомы выбора.

Однако, основная проблема заключается в неединственности продолжения Ji. Согласно нашему построению Ji определяется по продолжению L_fl функционала Вообще говоря, такое продолжение неединственно.

Следствие 5.1. Пусть Р — вероятностная мера, заданная на некоторой алгебре F подмножеств из Q. Тогда существует конечно-аддитивное продолжение Р вероятности Р на алгебру Fq всех подмножеств множества П.

Доказательство. По теореме Хана-Банаха 1 = Р (П) = ||/,|| = ||L,||. Поскольку, для каждого А? Fn, ||/л||ос = 1, мы получаем, что Р (Л) = Ь,(1_Л) < ||LJ||/лНос < 1. Следовательно, Р — конечно-аддитивная вероятностная мера. ?

В некоторых физических моделях мы можем использовать ‘вероятности', определенные на алгебре F& всех подмножеств множества П, которые получены посредством теоремы Хана-Банаха. Как это было ранее замечено, вообще говоря, эти вероятности не являются сг-аддитивны ми. Тем не менее, конечная аддитивность — только математическая проблема. Настоящей проблемой является неединственность продолжения Р. Например, мы начинаем с <7-аддитивности вероятности Р, определённой на <�т-алгебре Т. Давайте предположим, что некоторые события А? Fq Т имеют физический смысл. Пусть Pi и Р₂ различные продолжения одной и той же вероятности Р па алгебру Fa- В принципе, Pi (Л) Ф Р₂(Л) — Поскольку математических аргументов не достаточно для того, чтобы фиксировать ‘вероятность', нужно использовать некоторые дополнительные физические аргументы, чтобы получить ‘правильное продолжение'.

Оказалось, что ситуация с неединственностью намного сложнее. Как и в предыдущих рассуждениях, начнем с сг-адднтивной вероятности Р. определённой на <7-алгебре F. Пусть Р^ лебеговское продолжение вероятности Р на ег-алгебру J^rj_J измеримых no Лебегу множеств. Вероятность Р[, — единственное (Г-аддитнвное продолжение вероятности Р на F/,. С другой стороны, могут существовать конечно-аддитивные продолжения Р вероятности Р на F/_y, которые не совпадают с вероятностью Рц. Как мы уже не раз обсуждали, условие^{-аддитивности} является чисто математическим условием. Следовательно, с физической точки зрения нет причин выбирать только <7-аддитивные продолжения. Таким образом, стандартный выбор, Р^(Л), вероятности для событий А 6 Fi оказывается не таким естественным с физической точки зрения. Мы думаем, что некоторые парадоксы в квантовом формализме есть следствия общего мнения о том, что только лебеговское продолжение Рдаёт ‘правильную физическую вероятность¹. В частности, доказательство известного неравенства Белла основано на таком предположении. Таким образом, парадокс Эйнштейна-Подольского-Розеиа (см. главу 2) может быть следствием общепринятого (по, вероятно, не физического) выбора продолжения вероятности.

Мы обсудили продолжения вероятности, сохраняющие норму и полученные посредством теоремы Хана-Банаха. В принципе возможно существование продолжений Lfi: B (Q) -> R линейного функционала /_/(: С —> R которые увеличивают норму: ||?_/д|| > ||/_/д||. Если мы определим продолжение меры //: F —> R) с помощью такой процедуры продолжения, Ji (A) = L,(/д), А € Тц, тогда не может быть уверенности в том что мера Ji станет неотрицательной. В этом случае, начиная с вероятности Р: F —> [0,1] мы можем получить обобщенные вероятности Р: Fq —> R с отрицательными значениями так же как и со значениями большими 1. В главе 3 мы увидим, что такие обобщенные вероятности могут иметь физический смысл. Заметим, что если Р: F —> [0,1] (т-аддитивиая вероятность, то возможно, что (увеличивающее норму) продолжение Р: Fq —> R будет также <�т-аддитивным. В таком случае мы получаем знакопеременную вероятностную меру (заряд), см. главу 3.

Кроме того, может существовать увеличивающее норму продолжение Р сг-аддитивной вероятности Р (определенной на а-алгебре F) на лебеговскую сг-алгебру F^. Оно может быть таким, что Р (Л) 1) даже для некоторого А е Fl. Следовательно, даже для событий А е Fi, которые обычно рассматривались как ‘физические события', мы можем получить отрицательные обобщенные вероятности. Такие отрицательные вероятности имеют естественные ансамбль и частотные интерпретации (см. главу 3). Должны быть какие-либо специальные физические причины для рассмотрения только сохраняющего норму продолжения Р l вероятности Р на лебеговскую 17- алгебру FlЕсли нет таких причин, тогда, в принципе, мы имеем право использовать знакопеременные вероятности Р: Fl —> R для описания физической модели. Оказалось (см. главу 3), что имеются физические основания использовать такие знакопеременные меры (вместо стандартной вероятности P/J в некоторых физических моделях. В частности она может быть такой, что Р/,(Л) = Рl{B) = А, но Р (Л) ф Р (В). В этом случае мы можем расщепить обычную вероятность, А (задаваемую мерой Лебега) на несколько обобщенных вероятностей. В частности, нулевая обычная вероятность может быть расщеплена на множество обобщенных вероятностей (подробнее, см. главы 3 и 4).

Вернемся к плотности натуральных чисел.

Теорема 5.4. Плотность натуральных чисел 6: Gd —> [0,1] можно продолжить до конечно-аддитивной меры S: Fn —"• [0,1].

Доказательство. Опять применим теорему Хана-Банаха. Однако, поскольку Qa не является алгеброй, мы не можем непосредственно применить схему доказательства теоремы 5.1. Обозначим через ЫМ (N) подпространство нормированного пространства В (N) (всех ограниченных функций /: N —> R), состоящее из всех функций /, для которых существует среднее значение:

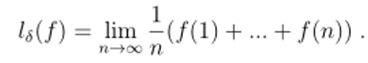
Отображение Is: ЫМ(N) —> R есть линейный непрерывный функционал и Is (Ia) = Для любого А € Gd- По теореме Хана-Банаха Is можно продолжить до линейного непрерывного функционала Ls: В (N) —> R и 1 = ?(N) = ls = ||L"$||- Положим ?(Д) = Ls (Ia) для А € F_N. Из линейности функционала Ls следует, что 6: Fn —> R аддитивно. Используя те же рассуждения что и в доказательстве теоремы 5.2, мы получим, что продолжение S неотрицательно. ?

Если А € Fn Gd, тогда.

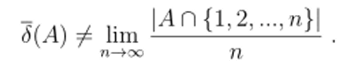
Следовательно, частотная идентификация события А невозможна (нарушается принцип статистической стабилизации; ср. с главами 2 и 4).

Продолжение 6 с нолуалгебры Gd на cr-алгебру Fn, данное теоремой 5.3, неединственно. Если в какой-нибудь физической модели некоторые множества А € Fn Gd рассматриваются как физические события, то должны быть специальные физические основания для выбора того или иного продолжения плотности S. А нам следует помнить, что принцип статистической стабилизации нарушается для событий А € Fn Gd- Как и в случае мер, определенных на алгебрах, может существовать продолжение L$ функционала Ц которое не сохраняет норму: ||L$|| > 1. В таком случае величина 6, соответствующая функционалу L&, может принимать отрицательные значения.

В принципе, мы пожалуй рассматриваем теорему 5.4 как ответ на вопрос А. Н. Колмогорова о возможности замыкания плотности натуральных чисел <5. Однако, Колмогоров хотел найти меру, которая замыкала бы плотность 5. Теорема 5.4 — неконструктивна (она основана на аксиоме выбора). В сущности она не даёт ответ на колмогоровский вопрос. Построение, которое использовалось в теореме 5.4 нельзя применить к произвольной полумере //. Таким образом, мы не знаем ответа на вопрос: «Возможно ли построить замыкание произвольной полумеры?» (ср. с Колмогоровым, 1929).