Электрические величины на комплексной плоскости

Как указывалось в параграфе 3.2, синусоидальную (гармоническую) электрическую величину — оригинал, например ток i = I_m sin (eo? ± j/) = = 421 sin (o)t ± |/), можно представить в виде радиус-вектора /," (или L = 1″, /42), «расположенного» первоначально на комплексной плоскости под углом ±|/, отсчитанным от вещественной оси в направлении против хода часовой стрелки, еслину (рис. 4.1), и — по ходу (на рис. 4.1), и вращающимся с угловой частотой (скоростью) со = 2л/ (см. рис. 4.1).

Тогда, с учетом рис. 4.1, можно записать оригинал и изображение тока так.

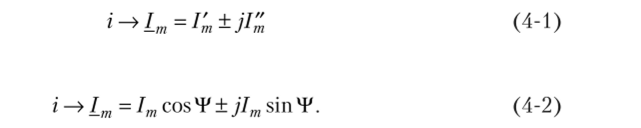
пли Изображения вектора тока/_ш, записанные в видах (4−1) и (4−2), называются соответственно алгебраической и тригонометрической формами комплекса. С учетом известной формулы Эйлера¹ е^±1^а = cosa± jsin, а их можно записать в третьей, показательной, форме:

Рис. 4.1.

В (4−3) регистрирует факт вращения вектора 1__т относительно начала осей координат против хода часовой стрелки со скоростью (частотой) о), «проходя» в любой момент времени t «путь», равный соt (рис. 4.1). Поэтому называется оператором вращения. При расчетах цепей его опускают (расчеты ведутся при t = 0). Его учитывают при переходе от комплексных изображений электрических величин к оригиналам.

В (4−1) e^v показывает, что вектор 1__т начинает свое вращение против хода (или по) часовой стрелки с положения, отстоящего от вещественной оси на угол ±ц/, т. е. вектор первоначально повернут на угол ±|/ относительно вещественной оси. Поэтому eJv называется оператором поворота. Его учитывают при расчетах цепей.

С учетом введенных понятий комплексные изображения электрических величин е = Е_т sin (cot + |/Д и = U_m sin (a)? — |/_w), i = I_m sinco^ временные диаграммы которых изображены на рис. 3.1, в трех формах запишутся так:

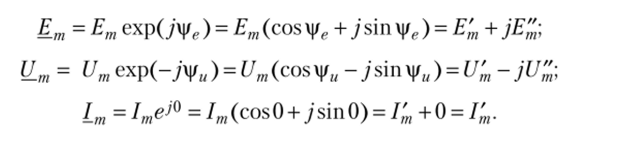
Иногда приходится электрические величины, записанные в дифференциальной и интегральной формах, изображать в комплексных формах. Например:

¹ Эйлер Леонард (1707—1783) — выдающийся математик, физик, механик, астроном. Родился в Базеле (Швейцария), много лет жил и работал в России.

Опустив в полученных выражениях оператор вращения e^±J^(0t₉ будем иметь.

Формула (4−4) показывает, что оригинал дифференцирования электрической величины заменяется векторным изображением (комплексным числом), умноженным наj (0, а интегрирования — делением наусо.

Как очевидно из рис. 4.1, модуль вектора 1__т есть отрезок, соединяющий начало осей координат 0 с точкой М с координатами /', = I_m cosy и I" = = I_m sin у, т. е. выражения «радиус-вектор на комплексной плоскости», или «комплексное число», или просто «комплекс» практически равнозначны.

Из рис. 4.1 также очевидно, что модуль радиус-вектора и начальную фазу, например 1_т и у, можно найти, если известна, например, алгебраическая форма записи комплексного числа: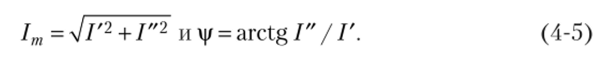

В (4−5) Г_т = I_m cosy — вещественная часть (составляющая) комплексного числа, обозначается через Rel_rn (Re — сокращенная запись английского слова real французского reel и немецкого real соответствующие русским словам — «реальный», «действительный», «вещественный»); /" = I_m sin у — мнимая часть комплексного числа, обозначается через 1т/," (1т — сокращенная запись английского слова imaginary, французского imaginare и немецкого imaginary соответствующие русскому слову «мнимый»).

Итак, синусоидальные электрические величины е, и_у i — оригиналы, можно изображать в виде комплексных чисел или радиус-векторов на комплексной плоскости Е_т = V2?, U__m = у[2Ц, I__m = V2/ соответственно. Если же известны изображения синусоидальных электрических величин Е_т, U__m, /_ш, то их оригиналы находятся как JmE__m, JmU__nr Jml__m.

Приведем некоторые полезные математические справки.

• 1. Два комплекса равны, если равны порознь вещественные и мнимые части и знаки между этими частями одинаковы, например а ± jb = с ± jd, если а = с и b = d.
• 2. Два комплекса являются сопряженными, если их вещественные части равны, а мнимые тоже равны, но с противоположными знаками, например комплексу а ± jb сопряжен комплекс a+jb и наоборот.
• 3. Произведение двух сопряженных комплексов равно квадрату модуля. Так, если М = 4а¹ +Ь², то (a±jb)(a + jb) = а² + Ь² = М². Доказательство: (<�а ± jb)(a + jb) = а² ± jab + jab + b² = а² + b² = М².
• 4. = ±j. Доказательство: = cos 90° ± j sin 90° = 0 ±j = ±j.
• 5. Умножение вектора на 6? W2 или на ±j соответствует повороту его на ±тт / 2 относительно вещественной оси, поскольку е^² = ± j.

Вопросы для самопроверки.

• 1. Как изображаются и записываются синусоидальные электрические величиныоригиналы в комплексной форме?
• 2. Чем заменяются оригиналы дифференцирования и интегрирования электрических величин?

Задача 4.1. Записать комплексные изображения мгновенных значений ЭДС е = = 282sin (со/ - л / 6), напряжения и = 141 sin cot и тока i = sin (coP+ 40°) для амплитудных и действующих значений в трех формах.

Решение

е^Е_т = 282е-/" /б= 282cosл/6-;282sinл/6 = 282 • 0,87->282 • 0,5 = (245->141) В,? = 282е->/6/^2 = 200cos л/ 6->200 sin л /6 = 200 • 0,87 ->200 • 0,5 = (174 -j 100) В; и -«?/>° = 141 В, и -> U = 141 / у/2 = 100 В; i -> /,» = сгАО = cos40° -j sin40° = (0,77 — -/0,64) А, г —> / = е-Р° / -J2= 0,71 cos40° ->0,71 sin 40° = 0,71 • 0,77 ->0,71 • 0,64 = = (0,55-/10,45) А.

Задача 4.2. Записать комплексы ЭДС Е_т = 310f/ⁱ⁰ В, напряжения С/ = (110 —> 191) В и тока / = 1 Л в видах мгновенных значений.

Решение

Для перехода от комплексных электрических величин к мгновенным значениям необходимо умножить комплексные амплитуды на е>^ш и взять коэффициенты при мнимых частях (1ш) от полученных произведений. Поэтому.

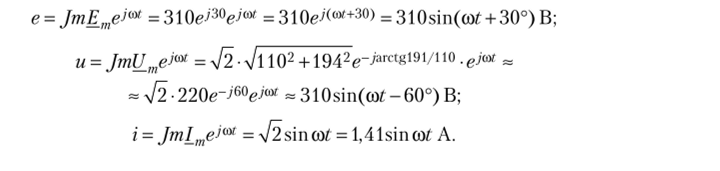
Задачи, требующие решения.

Задача 4.3. Записать мгновенные значения ЭДС е = 70sin ш/, напряжения и = = sin (co? — 20°) и тока i = 5 sin (со/ + 17°) в комплексных видах для амплитудных и действующих значений в трех формах.

Задача 4.4. Записать в показательной форме комплексы токов: 2,82 ±>1,4; 1,42 ± ± 2,82; -;6; 7.