Возврат из прерывания 2.9

Парадокс «Куча» можно кратко сформулировать так: добавление одного зерна к совокупности нескольких зерен, не образующих кучи, не делает эту совокупность кучей; следовательно, никакое число зерен не образует кучу.

Представляется, что этот парадокс можно разрешить, если использовать современное понятие нечеткого множества и считать множество возможных куч нечетким. Тогда добавление одного зерна к небольшой совокупности зерен просто увеличивает степень принадлежности этой совокупности к множеству куч. Трудно сказать, двигалась ли мысль античных логиков в направлении теории нечетких множеств или нет.

Заметим, что существует как бы обратная формулировка этого парадокса: удаление одного волоса с головы человека не делает его лысым.

Другому логику мегарской школы, Филону (не нужно смешивать его с двумя другими Филонами, которые уже упоминались выше), принадлежит теория так называемой материальной импликации — одной из трактовок логической функции «ЕСЛИ — ТО». В мегарской школе исследовались и другие трактовки этой функции [55, с. 24−26].

Переходя к Платону, выделим как одну из заметных сторон его учения теорию идей (историки философии выводят ее из сократовской практики выяснения содержания понятий). Очень кратко можно изложить эту теорию так: воспринимаемые нами веши являются воплощением вечных и неизменных — противостоящих гераклитовской текучести — идей, которые находятся как бы в особом мире, недоступном нашему восприятию. Но этот мир в какой-то степени доступен нашей памяти, поэтому познание есть своего рода воспоминание о мире идей. Получается, что основой познания является умозрение.

Но вместе с тем, как уже было отмечено в методологическом прерывании 2.3, Платон в нескольких своих произведениях высоко оценивал измерение (вернее, количественное сравнение) как источник объективных знаний и полагал, что можно измерять даже «приятное и тягостное» или «наслаждение и страдание» — чего мы до сих пор не умеем делать.

Выражение «платоновская идея» в настоящее время стало нарицательным; его часто употребляют в научных спорах — например, когда хотят сказать, что предлагаемое оппонентом понятие не связано с реальностью. Между тем само слово идея, как и некоторые другие, встречавшиеся нам раньше, имеет вполне земные корни — оно происходит от греческого глагола Seiv, означающего видеть [51, с. 13].

В. П. Зубов замечает, что Демокрит иногда называл идеями свои атомы, а также приводит ссылку на словарь Гесихия, где слово идея объяснено как подобие, форма, вид и наименьшее тело.

Полезно также знать, что в русских переводах античных авторов часто встречается слово эидос (оно уже попадалось нам в методологическом прерывании 2.8), равнозначное словам форма и вид. Со своей стороны одно и то же русское слово форма может стоять в разных местах переведенного текста вместо нескольких греческих слов, различающихся по значениям.

Поскольку Платон жил в то время, когда совсем свежа была память о противостоящих друг другу концепциях строения вещества, разработанных Эмпедоклом, Левкиппом и Анаксагором, он не мог не внести свой вклад в это противостояние.

Действительно, он предложил еще одну, совершенно оригинальную концепцию. Аристотель в восьмой главе первой книги трактата «О возникновении и уничтожении» пишет о ней так:

«Учение Платона отличается от учения Левкиппа тем, что, в то время как Левкипп признает неделимыми твердые [частицы], Платон признает таковыми плоскости; у Левкиппа неделимые твердые [частицы] различаются бесконечным множеством фигур, у Платона же [эти фигуры] ограничены [по числу], хотя и тот, и другой говорят о неделимых [телах], имеющих определенную фигуру» [53, с. 409J.

Эти платоновские плоскости, о которых Аристотель в разных местах вспоминает снова и снова, представляют собой треугольные грани или части граней правильных многогранников, составляющих, по мысли Платона, основу вещества. Пяти стихиям — земле, воде, воздуху, огню, эфиру — соответствуют пять правильных многогранников, и те стихии, частицы которых содержат в качестве граней треугольники одинаковой формы, способны превращаться друг в друга. Эта картина представлена Платоном в диалоге «Тимей»; ее краткое изложение можно найти в книге Зубова [51, с. 45—46].

Не очень вяжется с обликом Платона как абстрактного мыслителя свидетельство о том, что он устроил в Академии водяной будильник для ее участников.

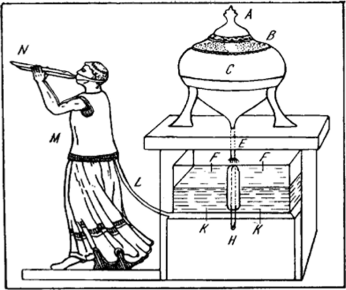
Будильник (рис. 2.14) действовал по принципу сифона. Вода, медленно вытекающая из верхнего сосуда красивой формы, постепенно заполняла средний прямоугольный _{Рис 2 14 Водяной будильник} Платона сосуд, в котором размещался сифон. Когда вода доходила до верхней точки сифона, он срабатывал и почти вся вода из среднего сосуда переливалась в нижний, вытесняя из него воздух. Вытесняемый воздух проходил через трубку, проведенную ко рту фигуры флейтиста, и раздавался звук флейты, который приглашал участников Академии на занятия. Таким образом, сифон в этой разработке, которую вполне можно назвать инженерной, действовал как пороговый элемент однократного срабатывания. Вряд ли Платон придумал это устройство сам; представляется более вероятным, что его предложил какой-нибудь его ученик.

В сочинениях Платона математики немного, но, тем не менее, говорят, что над входом в его Академию была надпись, запрещающая вход тем, кто не знает геометрию. Вероятно, Платон считал геометрию средством развития мышления об идеальных объектах. Б. Л. ван дер Варден пишет о Платоне так:

«Он руководил и воодушевлял научную работу как внутри, так и вне своей Академии. Великие математики Теэтет и Евдокс и все другие, перечисленные в каталоге Прокла, были друзьями Платона, его учителями в области математики и его учениками в области философии. Его великий ученик Аристотель, учитель Александра Великого, провел двадцать лет жизни в чудной атмосфере Академии» [19, с. 205].

Человеком, «который познакомил Платона с точными науками», Б. Л. ван дер Варден называет пифагорейца Архита из Тарента. Если верны данные о годах его жизни, Архит был на год старше Платона и умер тоже годом раньше. Платон встречался с Архитом в Италии, еще до основания Академии [44, с. 89—90].

Архит был исключительно многосторонним человеком. Он был государственным деятелем (говорили, что он не проиграл ни одного сражения). В области математики он внес вклад в решение различных проблем теории чисел; предложил, как уже говорилось в методологическом прерывании 2.4, довольно сложное построение с движущимися в пространстве фигурами для решения задачи удвоения куба. Он был также крупнейшим теоретиком музыки — ведь у пифагорейцев музыка была частью математики.

Б. Л. ван дер Варден, ссылаясь на Диогена Лаэрция, утверждает, кроме того, что Архит «был первым, кто дат систематическую разработку механики на математических основаниях». И при всем этом имеется много свидетельств о том, что он сделал деревянного голубя, который летал, и какую-то детскую трещотку [28].

Теэтет прославился открытием двух правильных многогранников — октаэдра и икосаэдра (куб, тетраэдр и додекаэдр были известны ранее), а также основательным исследованием различного рода иррациональностей — ван дер Варден насчитал 13 их видов [19, с. 235].

Сейчас историки математики записывают соответствующие выражения в буквенном виде, используя знак квадратного корня. Но Теэтет, как и его современники, мыслил геометрическими образами и говорил, например, об условиях несоизмеримости сторон квадратов, имеющих соизмеримые площади.

Нужно заметить, что греки строго соблюдали то, что мы сейчас назвали бы осмысленностью размерностей. Если некоторая величина рассматривалась как отрезок прямой, из нее нельзя было извлекать корень, не превратив ее предварительно в площадь с помощью вспомогательного отрезка единичной длины. Наоборот, произведение отрезков, имеющее размерность площади, нельзя было возводить в квадрат, так как квадрат площади не имеет геометрического смысла [Там же, с. 232—233]. Впоследствии математики отказались от этой строгости. Было ли это шагом вперед, как считают историки, или потерей — об этом, может быть, стоит задуматься.

Пожалуй, из окружения Платона наибольший интерес с позиций истории информационной сферы представляет Евдокс Книдский. По словам Б. Л. ван дер Вардена, «Евдокс был знаменит не только как математик, но и как медик, а прежде всего как астроном; кроме того, он был замечательным оратором, философом и географом» [19, с. 243]. После обучения в Академии и путешествия в Египет он основал собственную школу в Кизике, на южном берегу Мраморного моря [44, с. 97].

Евдокс, по-видимому, первым объединил длины отрезков, площади фигур и объемы тел общим понятием величины, которое сейчас (в еще более обобщенном виде) является одним из основных вообще в науке. Стаю возможным доказывать некоторые теоремы и формулировать аксиомы не отдельно для длин, площадей и объемов, а сразу для любых величин. Таковы, например, аксиомы (вероятно, принадлежащие Евдоксу), которые впоследствии были помещены в первую книгу «Начал» Евклида:

«Величины, равные одной и той же, будут равны и между собой. И если к равным прибавить поровну, то будут равны и суммы. И если от равных отнять поровну, то и остатки будут равны. И величины, совмещающиеся друг с другом, равны. И целое больше своей части» [ 19, с. 253].

Евдокс развил теорию отношении (в смысле ratio, а не relation), замечательную тем, что она была одинаково применима к соизмеримым и несоизмеримым величинам. Есть основания считать, что соответствующие определения из пятой книги Евклида тоже восходят к Евдоксу:

«Определение 3. Отношение есть некоторая связь по величине между однородными величинами.

Определение 4. Говорят, что величины находятся друг к другу в [некотором] отношении, если они, будучи взяты подходящее число раз кратными, могут превзойти одна другую.

Определение 5. Говорят, что величины находятся в том же самом отношении, первая ко второй и третья к четвертой, если любые одинаковые кратные первой и третьей будут одновременно обе или больше, или равны, или меньше любых одинаковых кратных второй и четвертой, взятых в соответствующей последовательности" [ 19, с. 258—259].

Последнее определение удобно представить в символьном виде:

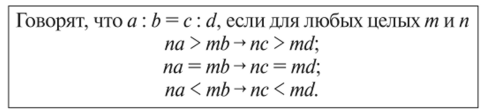
Если а и b (соответственно с и d) несоизмеримы, второй случай не будет иметь места ни при каких т и п.

Это определение по праву считается великолепным. Оно указало выход из того кризиса пифагорейской математики, который был вызван открытием несоизмеримости. Д. Я. Стройк пишет:

«Современная теория иррационального числа, построенная Дедекиндом и Вейерштрассом, почти буквально следует ходу мыслей Евдокса, но она открывает значительно более широкие перспективы благодаря использованию современных математических методов» [2, с. 63].

Однако мало кто замечает серьезный недостаток евдоксова определения равенства отношений: если представить его как алгоритм проверки справедливости пропорции, то придется перебрать всё бесконечное множество пар целых чисел тип.