Элементы векторного анализа

Пусть задано некоторое векторное поле а = а (г) (в каждой точке пространства задан вектор а) и некоторая поверхность S. Вектор а определен в каждой точке пространства, он определен и в каждой точке поверхности 5. Тогда величина.

называется потоком вектора, а через поверхность S. В математическом анализе рассматриваются способы вычисления таких интегралов для достаточно хороших подынтегральных функций, но в основе лежит представление об интеграле как о пределе суммы вида (5.5). Таким образом, объем, заметаемый поверхностью при малом смещении ее точек, равен потоку вектора смещения через эту поверхность.

Полученный результат дает ответ на вопрос задачи 5.2. Решение задачи 5.1 дает формулу для объема, проходящего за единицу времени через малую площадку (в пределах которой скорость можно считать постоянной). Обобщение этого результата на произвольную по величие поверхность приводит к формуле.

Задача 5.3. Жидкость течет по цилиндрической трубе, причем ее скорость зависит от расстояния от оси трубы по закону v® = v₀(l — r²/R²), где R — радиус трубы (как видим, у стенок, при г = R, скорость равна нулю, а на оси, при г = 0, скорость максимальна и равна v₀). Какой объем жидкости проходит через поперечное сечение трубы за единицу времени?

Решение. В плоскости сечения трубы выберем кольцо радиусом г, шириной dг. Площадь такого кольца dS= 2nrdr. В пределах кольца скорость v® одинакова, поэтому объем, проходящий через кольцо за единицу времени, будет равен v®d^ = v®? 2nrdr. Полный объем найдем, суммируя по таким кольцам, что приводит к интегралу.

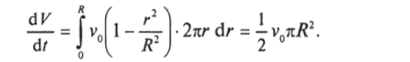
Более формально решение выглядит следующим образом. Введем цилиндрическую систему координат с осью z вдоль оси цилиндра. Для скорости имеем.

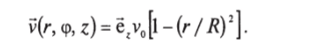
Поверхность интегрирования S — круг в сечении z = const, элемент поверхности в полярных координатах d5 = rdz-dcp, вектор нормали к элементу п (г, ч>) = ё_г. Формула (5.7) дает.

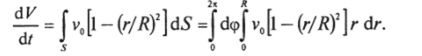
Интегрирование по углу немедленно осуществляется, и мы получаем старый результат.

При вычислении потока вектора через поверхность (формула (5.6)) особый интерес представляет случай замкнутой поверхности. Для обозначения интеграла по такой поверхности используют специальный знак При этом условились, что нормаль к элементу поверхности направлена наружу.

Представим себе неподвижную замкнутую поверхность в потоке жидкости и вычислим интеграл.

по этой поверхности, где v = v® — поле вектора скорости жидкости. Легко видеть, что в участках поверхности, для которых v • п < О, жидкость втекает в объем, ограниченный поверхностью, а где эта величина положительна, жидкость вытекает из объема (нарисуйте картинку и убедитесь в этом). Весь интеграл представит разность между вытекающим и втекающим объемами жидкости за единицу времени. Ясно, что, если жидкость несжимаема, эти объемы должны быть равны и интеграл равен нулю. Верно и обратное утверждение: если поток вектора скорости через любую замкнутую поверхность равен нулю, объем любого элемента жидкости не изменяется.

С другой стороны, рассмотрим некоторый элемент движущейся жидкости, ограниченный замкнутой поверхностью. Пусть S — положение в пространстве этой поверхности в момент времени t. В момент времени I + d/ поверхность займет новое положение, причем вектор смещения точек поверхности будет, очевидно, vd/, где v — вектор скорости жидкости в соответствующей точке поверхности в момент времени t. Согласно формуле (5.5),.

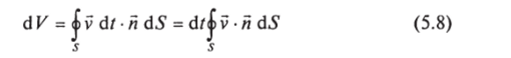
есть объем, заметаемый всеми элементами поверхности за время d/. При этом объем, соответствующий элементам поверхности, для которых v • п > 0, прибавляется к исходному объему, а для которых.

v • п < 0 — вычитается. Таким образом, формула (5.8) дает изменение за время At объема движущегося элемента жидкости.

Нам понадобится еще понятие объемного интеграла. К нему приводит такая, например, проблема. Распределение вещества в пространстве характеризуется плотностью. Эта величина вводится следующим образом. В окрестности некоторой точки г рассмотрим малый элемент объемом Д V, и пусть масса вещества в этом элементе равна Ат. Вычислим отношение Ат/А V и рассмотрим предел этого отношения при уменьшающемся А V. Этот предел существует и называется плотностью вещества в точке г:

Смысл этой величины состоит в том, что если мы выберем малый элемент объема в окрестности точки г, то масса этого элемента Ат = р (г)дК. Задание скалярной функции р = р (г) полностью определяет распределение массы в пространстве.

А теперь такая проблема. Пусть в пространстве задана плотность массы р = р (г). Рассмотрим некоторый объем Vw зададимся вопросом: как найти массу, содержащуюся в этом объеме? Решение следующее. Разбиваем объем на малые элементы, настолько малые, что в пределах элемента плотность можно считать постоянной. Пусть г. — точка, в окрестности которой находится элемент объемом AV_r Масса этого элемента Ат, = p (r.)A V_r Полная масса в объеме найдется как сумма масс всех элементов: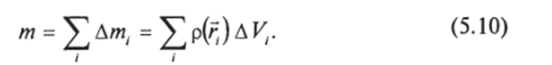

Результат тем точнее, чем на меньшие элементы разбит весь объем. Переходя к пределу, будем иметь.

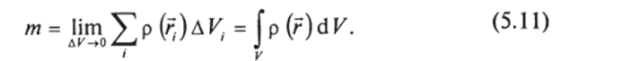
Интеграл в последнем равенстве можно рассматривать просто как обозначение предела суммы. Обратите внимание на структуру выражений под знаком суммы и интеграла. В математическом анализе рассматриваются способы вычисления объемных интегралов для достаточно хороших подынтегральных функций и областей интегрирования.

Задача 5.4. Плотность воздуха в атмосфере зависит от высоты по.

_и_

закону р = р₀е «, где Н ~ 8 км. Какова масса столба воздуха сечением S и неограниченной высоты?

Решение. Разобьем столб воздуха на горизонтальные слои с малой толщиной, так что в пределах слоя плотность можно считать постоянной (для этого толщина слоя должна быть много меньше 8 км). Пусть i -й слой находится на высоте й_#, его толщина Ah_r Масса.

Aj_.

этого элемента Ат. = р (Д,)ДИ, = р₀е'" 5 ДА,. Масса всего столба найдется как сумма масс слоев:

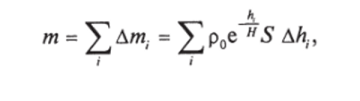
что приводит к интегралу.

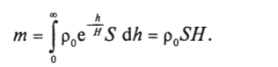
Видим, что масса столба такая же, как у столба высотой Я с плотностью р₀ (плотность у поверхности Земли). Эффективная толщина атмосферы оказывается много меньше радиуса Земли.

Для векторного поля определена операция под названием дивергенция векторного поля, которая векторному полю ставит в соответствие скалярное поле:

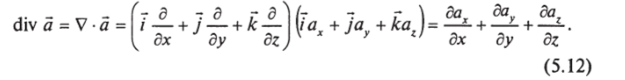
(5.12).

Значение скалярной величины div а в любой точке зависит от поведения векторного поля а в окрестности этой точки.

Задача 5.5. Найти дивергенцию векторного поля a (r) = ar, а = const.

Решение. Как видим, вектор а в любой точке направлен вдоль луча, проведенного из начала координат через эту точку, а его модуль пропорционален расстоянию до начала координат. Имеем:

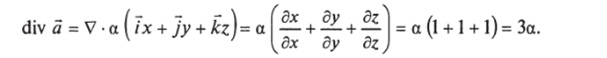
Смысл и значение введенной операции проясняется следующей важной и не очевидной теоремой Остроградского—Гаусса:

поток вектора через замкнутую поверхность равен интегралу от дивергенции этого вектора по объему, охваченному этой поверхностью.

Это довольно удивительная теорема. Пусть мы имеем векторное поле, заданное в некоторой области пространства. Выберем в этой области замкнутую поверхность. В точках этой поверхности вектор имеет определенные значения, и по ним можно вычислить поверхностный интеграл (поток вектора). В то же время можно вычислить дивергенцию этого поля во всех точках внутри выбранной поверхности и вычислить от нее интеграл по объему («количество» дивергенции в этом объеме). Теорема утверждает, что полученные величины совпадут. Но представим теперь, что мы непрерывно меняем векторное поле внутри объема, но так, что его значения на поверхности не меняются. Дивергенция в каждой точке при этом меняется, но интеграл по объему от нее не изменяется! Это своего рода математический закон сохранения, имеющий отношение к физическим законам сохранения.

Задача 5.6. Вычислить для векторного поля из задачи 5.5 поток через поверхность сферы радиусом R с центром в начале координат.

Решение. Имеем:

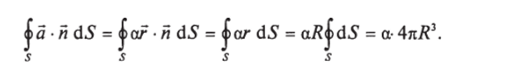
(Учтено, что направление векторов г, п совпадает во всех точках сферы г = R и Jd5 по поверхности есть площадь этой поверхности.).

Задача 5.7. То же, что и в предыдущей задаче, но центр сферической поверхности не совпадает с началом координат.

Решение. В этом случае вычислить интеграл по поверхности не так просто: направление векторов а, п в разных точках поверхности не совпадает (нарисуйте картинку), скалярное произведение этих векторов в разных точках поверхности разное и не может быть вынесено из-под знака интеграла. Воспользуемся теоремой Гаусса:

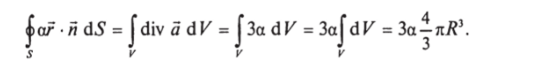
(Использован результат, полученный в задаче 5.5.) Таким образом, для данного векторного поля поток через сферическую поверхность не зависит от положения этой поверхности! Результат вовсе не очевидный. Легко сообразить, что это связано с тем, что дивергенция рассматриваемого поля постоянна, и становится ясным, что в этом случае поток через любую замкнутую поверхность не зависит от ее положения.

Задача 5.8. Для векторного поля а (г) = а г 1 — ^1 — вычислить интеграл от дивергенции по объему шара радиусом R с центром в начале координат.

Решение. Можно, хотя и хлопотно, вычислить дивергенцию этого поля и соответствующий объемный интеграл (постарайтесь это сделать). Однако результат можно написать сразу, если заметить, что в точках поверхности г = R это поле совпадает с полем из задачи.

5.6, и воспользоваться теоремой Гаусса. Но этот трюк, очевидно, не пройдет, если центр шара не совпадает с началом координат.