Конечный элемент балки в условиях плоского изгиба

Построим матрицу жесткости двухузлового балочного элемента для решения задач плоского изгиба. Элемент содержит два узла. Локальная ось х направлена от узла 1 к узлу 2. Локальная ось у соответствует правосторонней системе координат. В каждом узле возможны два перемещения: линейное перемещение v вдоль оси у и поворот 0 вокруг оси z. В дальнейшем для удобства при соответствующих ссылках будем использовать термин «обобщенные перемещения». Обобщенным узловым перемещениям соответствуют обобщенные узловые усилия/и т. Знаки обобщенных перемещений определяются правилами, установленными для правосторонней системы координат (рис. 9.10).

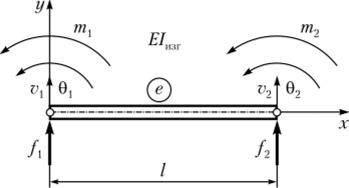
Рис. 9.10. Двухузловой балочный элемент для случая плоского изгиба

Вектор узловых перемещений и вектор узловых сил конечного элемента запишутся в виде.

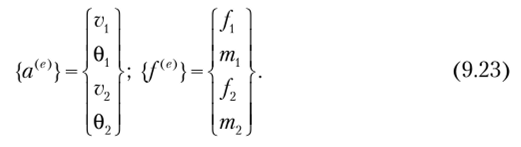
Уравнение равновесия конечного элемента запишется в стандартной форме.

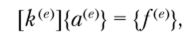
где |/v^,('⁾] — матрица жесткости конечного элемента размерности 4×4.

Для определения компонент матрицы жесткости воспользуемся методом прямых жесткостей. При проведении первого теста зададим единичное перемещение по первому обобщенному направлению v_t = 1, запретив перемещения по всем остальным обобщенным направлениям (рис. 9.11).

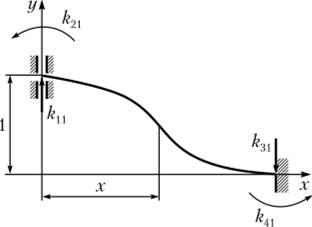
Рис. 9.11. Единичное перемещение по первому обобщенному направлению

По определению, возникшие при таком нагружении обобщенные усилия будут численно равны компонентам первого столбца матрицы жесткости элемента. Для определения усилий воспользуемся дифференциальным уравнением изогнутой оси балки (7.7):

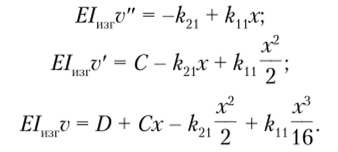
Уравнение содержит четыре неизвестные постоянные величины, для определения которых воспользуемся граничными условиями:

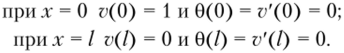
После подстановки граничных условий в уравнение находим компоненты первого столбца матрицы жесткости:

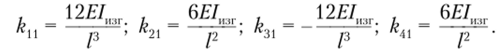
Для определения компонентов второго столбца проведем второй тест. Зададим в первом узле угол поворота 0, = 1. Остальные обобщенные перемещения запретим (рис. 9.12).

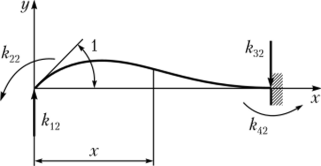
Рис. 9.12. Единичный угол поворота в первом узле

Интегрируя дифференциальное уравнение изогнутой оси балки, получаем.

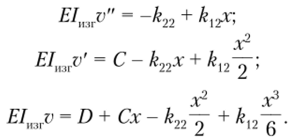
Для определения постоянных величины используем граничные условия:

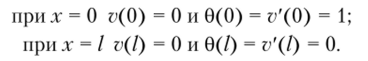
После подстановки граничных условий в уравнение находим компоненты второго столбца матрицы жесткости:

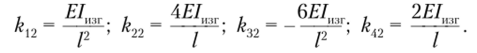
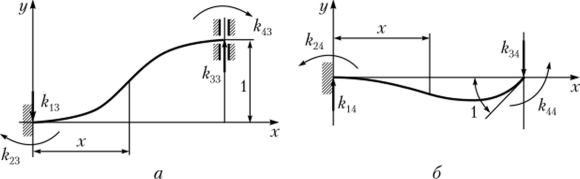
Pmc. 5. 73. Иллюстрация третьего и четвертого тестов

Третий (рис. 9.13, а) и четвертый (рис. 9.13, б) тесты проводить не будем, поскольку очевидно, что абсолютные значения компонент матрицы будут такими же, как в первых двух тестах. Уточнения потребуют только знаки.

Окончательно получаем матрицу жесткости конечного элемента в следующем виде:

Отметим, что локальные индексы в матрице жесткости балочного элемента изменяются от 1 до 4.

В качестве примера рассмотрим расчет упругой системы, состоящей из двух балок различной жесткости и упругой пружины (рис. 9.14).

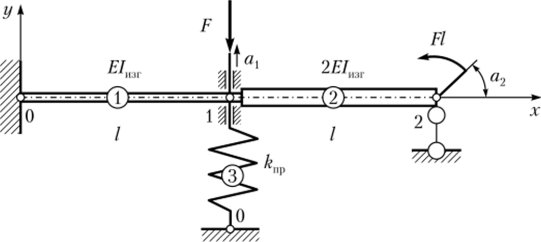
Рис. 9.14. Система из двух балок различной жесткости и упругой пружины

Конструкция содержит три элемента. Элементы 1 и 2 являются балочными элементами, элемент 3 представляет собой пружину, которую рассматриваем как конечный симплекс-элемент, работающий па растяжение-сжатие.

2Е1

Для определенности положим k_np = ——-*^-^г. При глобальной нумерации узлам, в которых запрещены перемещения, присвоен номер 0. Таким образом, рассмотрению подлежат два узла. В узле 1 разрешено только вертикальное перемещение a_v В узле 2 разрешен угол поворота а₂. В узле 1 приложена сосредоточенная сила F, действующая в отрицательном направлении, а в узле 2 — положительный изгибающий момент. Таким образом, разрешающая система для ансамбля конечных элементов будет иметь вид.

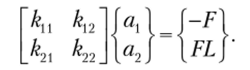
Составим матрицу соответствия индексов (табл. 9.3).

Таблица 93

Матрица соответствия индексов для рис. 9.14

Выпишем матрицы жесткости отдельных элементов и произведем их индексное окаймление:

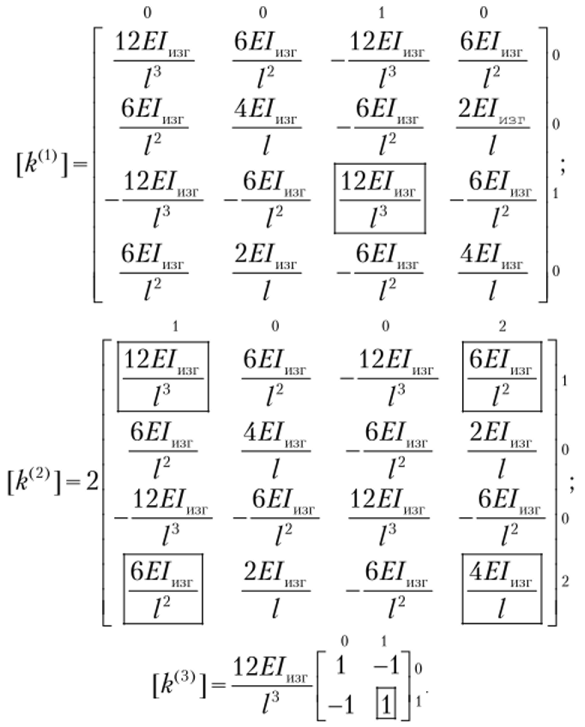
Проведем сборку глобальной матрицы жесткости ансамбля конечных элементов (компоненты, стоящие в локальных позициях, которым соответствует нулевой глобальный номер строки или столбца, в сборке не участвуют):

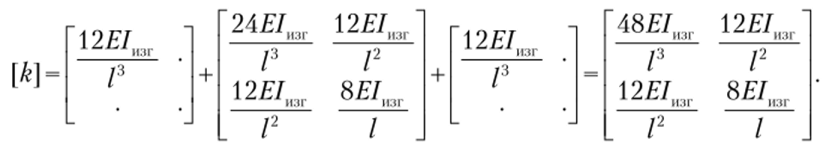
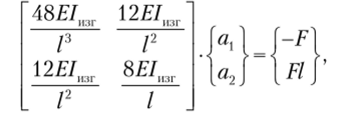
FP F1²

«ах0ДИМ01._;0!._

Подсчитаем обобщенные усилия в элементе 1:

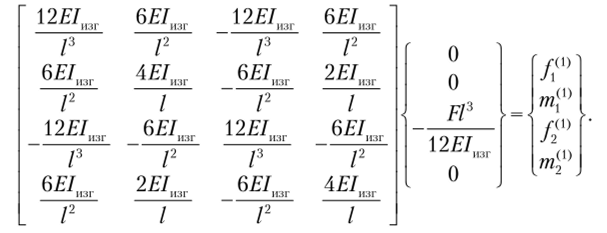
Решая систему алгебраических уравнений, находим 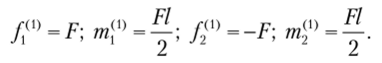Узловые усилия, возникающие в элементе 1, показаны на рис. 9.15.

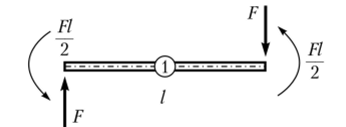
Рис. 9.15. Узловые усилия в элементе 1.