Конечный автомат как формальная модель системы. 
Обучение автоматов

При обсуждении методов построения математических моделей ФХС с точки зрения распознавания образов (см. стр. 86) отмечалось, что один из возможных путей формального описания ФХС состоит в конструировании распознающего устройства, которое прогнозирует поведение системы так же, как это делал бы соответствующий функциональный оператор. Достоинство такого «конструктивного» подхода к решению поставленной задачи состоит в его инвариантности к изменению внутренних характеристик системы и виду ее аналитического описания. Математический аппарат, адекватный данному подходу, находится на стыке нескольких дисциплин: распознавания образов, теории вероятности и математической статистики, алгебры логики, теории конечных автоматов.

Примером решения задачи указанным методом может служить работа [48], где описывается самонастраивающаяся система управления распределением температуры воды в технологическом аппарате, главным элементом которой служит обучающийся дискретный автомат. Обучающийся автомат, построенный на пороговых элементах, распознает состояние процесса по данным текущих измерений его параметров и отвечает определенной совокупностью управляющих воздействий, что обеспечивает оптимальное протекание процесса. Известно также применение для указанных целей распознающих систем, в основе которых лежат адаптивные конечные автоматы или персептроны на пороговых элементах типа «Адалина», «Альфа» и др. [4, 49—51 ].

Конечный автомат. Конечный автомат представляет частный случай динамической системы, определенной выше (см. стр. 108). Как и динамическая система, он характеризуется тройкой векторов: входных воздействий и, состояний х п выхода у, однако в данном случае множество возможных значений каждого из векторов конечно. Обозначая эти множества соответственно U, X, У, можно записать.

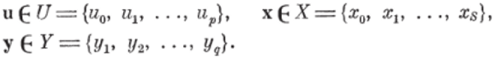
Поведение конечного автомата обычно задается в одной из трех форм: аналитической, табличной или графической. Аналитическое описание детерминированного автомата состоит из двух уравнений: уравнения перехода (<состояния) и уравнения выхода:

Здесь к — номер временного интервала (время квантуется на равные интервалы); индекс у функций f_r (•) и <�р_г (•) означает, что функции квантованы по уровням и принимают значения из соответствующих конечных множеств X и У.

Табличную и графическую формы представления детерми— / ованного автомата проиллюстрируем на конкретном примере.

Принцип табличного представления понятен из структуры табл. 2.6. Диаграмма перехода, соответствующая табл. 2.6, показана на рис. 2.4. Узлы диаграммы соответствуют состояниям, а связи между узлами — переходам.

Обобщением детерминированных автоматов являются стохастические автоматы, которые характеризуются вероятностями переходов из одного состояния в другое. Аналитическое описание стохастического автомата имеет вид.

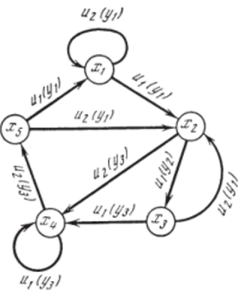
Рис. 2.4. Диаграмма перехода автомата, заданного табл. 2.6.

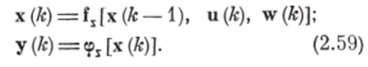
Здесь w (к) — случайная решетчатая функция (например, бернуллиева, у которой вероятность появления той или иной дискреты фиксирована и пе зависит от появления других дискрет).

В связи с обучением автоматов при построении распознающих устройств необходимо учитывать взаимодействие автомата с окружающей средой. Для этого вводится уравнение среды

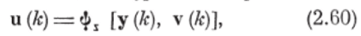
где Фх (•) — некоторая квантованная по уровню функция; v (к) — случайная решетчатая функция возмущений среды. Совокупность уравнений (2.59), (2.60) отражает взаимодействие автомата со средой: действия автомата у (к) вызывают ответпую реакцию среды и (/с), которая, в свою очередь, воздействует на автомат.

Обучение автоматов. Ключевой проблемой, возникающей в связи с взаимодействием автомата с окружающей средой, является изучение влияния среды на поведение автомата, исследование возможности приспосабливания автомата к внешним условиям и целенаправленного улучшения этого приспосабливания. Количественный анализ перечисленных вопросов требует прежде всего определения меры целесообразности поведения автомата. С этой целью поведение автомата подразделяют на три вида: благоприятное, неблагоприятное и безразличное и избирают метод поощрения или штрафования за тот или иной вид поведения. Например, благоприятным считают такое поведение, при котором ответная реакция среды переводит входное воздействие в нуль и (/с)=0, а неблагоприятным — когда и (А)=1. Код 0 или 1 считают соответственно поощрением или штрафом, а математическое ожидание р=М {и } — мерой целесообразности поведения автомата [4). Ситуация, когда выход автомата является бернуллиевой решетчатой функцией у (к)=Ь (к), соответствует безразличному поведению автомата. В этом случае мера целесообразности поведения равна условному математическому ожиданию р₀=Л/{и/у=Ь}. Отсюда естественно считать, что автомат характеризуется целесообразным поведением, если р < р₀.

В задачах обучения автоматов ставится требование не только целесообразности (т. е. выполнения условия р < р₀), но и оптимальности их поведения, при котором математическое ожидание штрафа должно быть минимальным. Различают два способа выполнения этих требований: 1) перестройка структуры преобразователя сигнала х (к) в у (А:), т. е. вида функции s (•); 2) перестройка структуры самого автомата, т. е. изменение вида функции МО;

Первый способ состоит в минимизации меры р=М {и} выбором функции (p_s (х). Рассмотрим схему решения этой задачи на примере автомата с одним входом и одним выходом (заметим, что векторный случай легко сводится к скалярному простым кодированием переменных). С учетом уравнений (2.59), (2.60), записанных в скалярной форме, основное условие оптимальности принимает вид.

Поиск характеристики преобразователя <�р, (я) можно свести к выбору постоянных коэффициентов a_lt а₂, …" ах, задавая <�р_х (х) в виде конечной линейной комбинации.

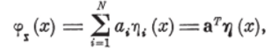
где r_f (x)=i при x=x_i и (я)=0 при х*?х_{.

Минимизация получающегося при этом функционала / = М {ф_х[а^тт2 (я), и]} выполняется в соответствии с рассмотренными ранее алгоритмами адаптации (см. стр. 84) путем обработки реализаций поведения автомата.

Второй способ обучения автомата (перестраивается его внутренняя структура) проиллюстрируем конкретным примером решения задачи оптимального прогнозирования поведения некоторой системы.

Построение автомата, прогнозирующего поведение ФХС.

(52—54]. В качестве примера рассмотрим схему построения распознающего устройства, позволяющего прогнозировать и управлять температурным режимом стекловаренной печи системы вертикального вытягивания стекла лодочным способом [52]. Стекловаренная печь — характерный пример сложной ФХС, для описания поведения которой в известной мере оправдан подход с позиций «черного ящика».

В практической реализации распознающих систем важную роль играет метод кодирования переменных. Обычно для этой цели используется двузначное кодирование (49, 50]. Для объектов химической технологии, характеризующихся существенной инерционностью и непрерывностью изменения технологических параметров, иногда целесообразно трехзначное кодирование траекторий переменных [53, 54]. Пусть Дt — интервал временного, а Д/г — интервал уровневого квантования переменной х. Тогда значение переменной в момент T=NAt вычисляется по формуле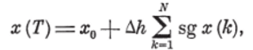

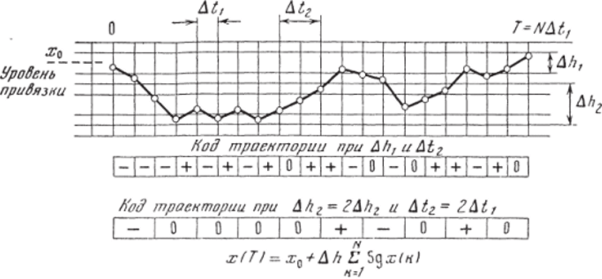
Рис. 2.5. Приыции кодирования траектории параметра.

где х₀ — начальное значение переменной («уровень привязки»); sg х (к) — знак, определяющий движение переменной по уровням квантования в к-й интервал времени; «+» — переход на один уровень вверх; «•—» — переход на один уровепь вниз; «О» — переменная остается на том же уровне, что и в интервале (к—1). Таким образом, траектория параметра па отрезке времени (О, Т ], исходящая из уровня привязки х₀, представляется последователь* ностью типа —1, —1, —1, +1, —1, …" или в более простой записи:——1—- • • (см. рис. 2.5). Кодирование перемен ных сводится к определению на каждом временном интервале Д/д. соотношений между х (А:—1) и х (к) по правилу.

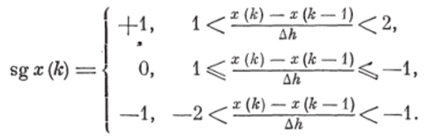
Идея построения автомата, использующего трехзначное кодирование информации, состоит в том, что на основе анализа ограниченного участка траектории параметра вырабатывается некоторый прототип (или эталон) переключения для каждого из трех возможных знаков кода и сравнением по мере близости с траекторией параметра определяется знак управляющего воздействия или прогнозируется знак движения управляемой (наблюдаемой) координаты. Подобный автомат оптимальным образом переучивается (меняет структуру) на каждом временном интервале движения процесса, что позволяет сделать его инвариантным к изменениям характеристик процесса и средств его контроля.

Рассмотрим процедуру формирования эталонов переключений для траектории параметра (температуры стекломассы) вида (см. рис. 2.5).

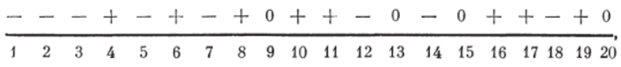
где N=20 — длина предыстории процесса. Существо процедуры состоит в построении матриц предыстории переключения, представляющих корреляционные поля для каждого из трех возможных знаков кода в траектории параметра. Принцип построения матриц предыстории переключения ясен из рис. 2.6. Закон корреляции здесь определяется как последовательность временных интервалов, отделяющих один и тот же знак в траектории параметра (т. е. однозначно характеризуется рельефом склона матриц предысторий). Столбцы матрицы предысторий будем называть признаками. Формирование эталона (прототипа) переключения сводится к выбору знаков полюсов (областей притяжения кодов признаков), обеспечивающих наибольшую меру близости между эталоном и предысториями переключения данного знака. Выбор знака каждого разряда эталона производится по большинству «+» или «—», входящих в столбец матрицы переключения (см. рис. 2.6).

Распознающие свойства эталонов переключений проверяются на той же обучающей последовательности. Для этого строки корреляционных матриц сравниваются последовательно с каждым из трех эталонов «4-», «О» и «—» и вычисляются соответствующие меры сходства. В качестве меры сходства (близости) траекторий к прототипам переключений используются (как наиболее простые) меры типа скалярного произведения х Д р

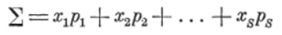
и меры типа расстояния по Хеммингу | х—р | (501.

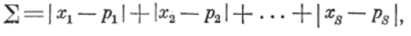
где х_{ и р_{ — код траектории и эталона соответственно. В случае ситуации равновероятного выбора (обозначена «4;») знак выбирается либо с помощью генератора случайных чисел, либо с использованием некоторого решающего правила, либо принимается знак последнего разряда столбца матрицы. Как видно из рис. 2.6, проверка прототипов на обучающей последовательности дала 13 правильных и 3 «возможно» правильных ответа из 19 предъявленных траекторий — строк матриц переключений, что соответствует примерно 25% ошибок. Видно, что правильно опознаны траектории 4-^-8, 10, 134−15, 174−20 (принята сквозная нумерация строк матриц). Ответ при показе траекторий 3, 9 и 12 определялся С помощью генератора случайных чисел. Характерно, что с уве;

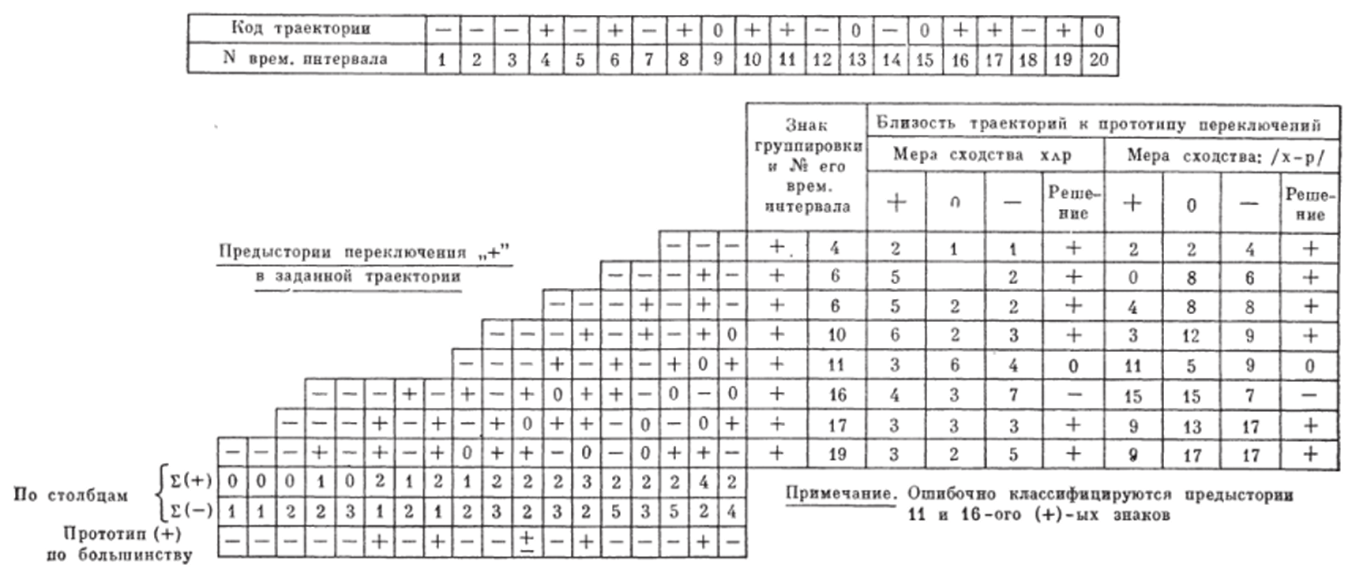
Рис. 2.6. Формирование матриц предысторий переключения «+*, «0» и «—* и результаты классификации предысторий с помощью прототипов личением числа учитываемых признаков (длины предыстории) процент правильных решений повышается.

Чтобы выполнить собственно прогноз, нужно исходную траекторию параметра (см. рис. 2.5) сравпить с каждым из трех построенных эталонов переключений «+», «О», «—» и вычислить соответствующие степени сходства. Решение определяется наибольшей степенью сходства. В данном случае к исходной траектории наиболее близок прототип переключения «-[-», что и определяет знак прогноза параметра.

Точность прогноза существенно повышается, если вместо выбора знаков полюсов эталона по большинству «-{-» или «—» в столбцах признаков применить аналогичную операцию прогнозирования знака для траектории каждого столбца. Это значит, что для каждого столбца матриц строится «своя» тройка эталонов «4-», «О» и «—», по которой осуществляется прогноз. Эти эталоны естественно назвать вторичными в отличие от первичных, соответствующих исходной траектории. Ту же процедуру можно применить для матриц, связанных с вторичными эталонами, и т. д. Таким образом, получается иерархическая структура распознавания.

Первый уровень образуют три эталона переключений исходной траектории параметра. Второй уровень составляют прототипы переключений для траекторий первичных признаков — три прототипа на каждый полюс эталона первого уровня. Третий уровень составляют эталоны переключений для траекторий вторичных признаков и т. д. до уровня, в котором эталоны формируют свои полюса по траекториям признаков, содержащим 1, 2, 3,.. ., т кодов, где т — заданное число, начиная с которого (в сторону уменьшения) знак полюса выбирается согласно следующей таблице решающих правил (табл. 2.7).

Таблица 2.7.

Перссптронная структура алгоритма (см. рис. 2.7) [54]. Изложенная выше схема решения является одним из вариантов персептронных структур. Исходная траектория в трехзначном коде.

(+1, О, —1) рассматривается как сенсорный 5-слой, состоящий из N элементов, которые соединяются связями с элементами (или компонентами) первого ассоциативного слоя Л_х. Направление связей и число Л^элементов зависят от заданной величины т и законов корреляции знаков в траектории параметра,^{-элементы} представляют собой логические блоки, использующие решающие правила выбора знака полюса (см. табл. 2.7), и имеют один выход, по которому передается сигнал знака на следующий слой А ₂- Каждый элемент слоя Л₂ выполняет функцию определителя меры сходства между знаком полюса и соответствующим ему знаком 5-элемента и имеет два входа и один выход, где формируется сигнал меры сходства. Одна часть Л₂-элементов, которые объединены в группы эталонов, связаны с компонентами слоя Л₃, где сигналы от группы компонент А_г суммируются. Другая часть Л₂-элементов непосредственно связана с компонентами высших слоев, где они входят в состав групп эталонов. Элементы слоя Л₃ объединяются по три в слое Л₄, в котором происходит сравнение сигналов, поступающих из слоя Л₃, и выбор по максимуму условной вероятности одного из трех знаков кода, который передается в слой Л₅. Компоненты слоя Л₅ выполняют те же функции, что и компоненты Л₂: они определяют меру сходства пары, образованной элемептом слоя Л₄ и одной из компонент сенсорного слоя, а также вырабатывают сигнал, поступающий на сумматор слоя Л₆ (так же, как от А₂ на А₃). Последний слой ассоциативных элементов содержит три элемента, подобных компонентам слоя А₃. Объединение выходов из них реализуется в одном Л-блоке, который работает аналогично элементу Л₄ и производит окончательную классификацию входного изображения на три класса: «+1», «О» и «—1».

В описанном типе персептрона существуют два следующих друг за другом режима работы: начальный (или подготовительный) режим и режим решения. В период подготовительного режима производится установление связей между 5- и Л-элементами по правилам построения корреляционных матриц. Во время второго режима решаются одновременно две задачи: формирование эталонов и принятие решения. В рассмотренной структуре персептрона отсутствует система подкрепления связей. Это объясняется тем, что перед данным персептроном стоит задача произвести классификацию изображения по трем классам только на основании анализа самого изображения. При смещении «окна» предыстории на один такт происходит переориентация связей между 5- и Л-элементами.

Оценка эффективности поведения автомата. Изложенный подход позволяет построить модель ФХС в виде обучающегося конечного автомата, основанного на корреляционных матрицах переключений для траекторий входного и выходного сигналов. Состояние автомата описывается тремя векторами признаков — полюсов х₊, х₀, х_ для каждого знака переключения выходной.

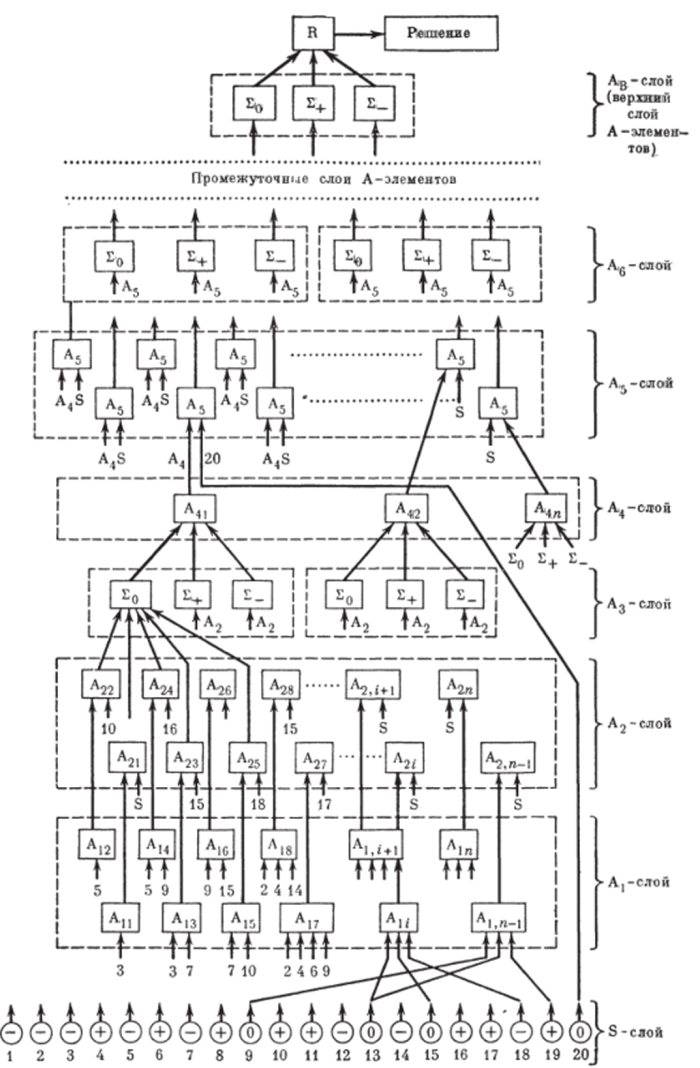
Рис. 2.7. Персептронная структура алгоритма предсказания координаты. Уравнение такого автомата можно записать в виде (2.58).

где у (&+1) — знак выходного параметра на (Л+1)-м шаге; р (и (/с), х_и (к))— мера сходства вектора признаков входного сигнала и (к) и вектора полюсов его состояния х_и (к) на к-м шаге для трех возможных знаков переключений выходной координаты на (Л+1)-м шаге; р (у(к), х_у (А:)) — мера сходства вектора признаков выходного сигнала у (к) и вектора полюсов его состояния х_у (к) на к-м шаге для трех возможных знаков переключений выходной координаты на шаге; X — пороговое значение решающего правила отбора полезных признаков; А — пороговое значение решающего правила выбора знака у (A:-f-l).

Введем фупкцию потерь C_tJlр (у (Аг+1), у₀ (Л+1))], где р (у, у₀) — мера сходства кодов выходного сигнала объекта у₀ (/с+1) и автомата у (Л+1). Величины Собразующие платежную матрицу.

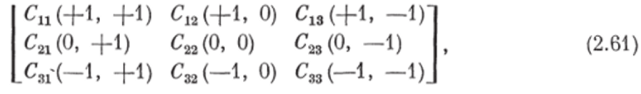
характеризуют потери, возникающие при отнесении автоматом приращения выходного параметра на (&+1)-м шаге к одному из трех классов: -j-1, 0, —1. По главной диагонали платежной матрицы расположены потери при правильных решениях, по обеим сторонам от нее — потери от ошибочных решений.

Суммарные потери определяются величиной среднего риска:

где P_t, Р_2У Р₃ — вероятности появления знаков 1, 2, 3 в выходном сигнале объекта; р (]/i) — условная вероятность появления знака j в выходном сигнале модели при наличии знака i в выходном сигнале объекта.

Заменяя ипдексы 1, 2, 3 на «+», «О», «—», запишем соотношение (2.62) в более наглядной форме:

Ёсли принять диагональные значения функции штрафа при правильном распознавании равными нулю С₊₊=С^,₀₀=С._=0, то получим выражение.

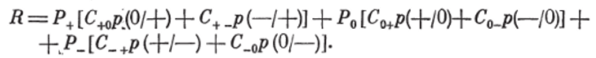
При постоянных значениях функций шрафа C_{j и вероятностей Р₊, Р₀₁ минимум среднего риска достигается минимизацией условных вероятностей.

Если компоненты матрицы шрафо в (2.61), расположенные по обе стороны диагонали, одинаковы, например равны единице, то минимум среднего риска достигается максимизацией вероятностей правильных распознаваний:

Настройка обучающейся модели осуществляется поиском значений Х_оит и Д_011Т на основе ограниченных предысторий входного и выходного параметров, чем достигается выполнение условий (2.63) и (2.64) для оценок апостериорных вероятностей р (J/k) решений модели.

? * *.

В данной главе были рассмотрены некоторые характерные приемы формального построения функционального оператора ФХС на основе принципов «черного ящика», когда единственно доступной информацией об объекте являются его входные и выходные сигналы. В качестве результирующего функционального оператора в 'анном случае могут выступать модели, построенные на базе идей адаптации и обучения, уравнения регрессии и булевы модели (преимущественно при описании статического состояния ФХС), уравнения пространства состояний (при описании динамического поведения ФХС), специальные распознающие устройства, обучающиеся автоматы или любая другая форма описания, получаемая на основе анализа и обработки внешних информационных характеристик объекта.

Характерная черта этого подхода состоит в абстрагировании от внутренней структуры ФХС и тех законов, которым подчиняются физико-химические процессы, протекающие в системе. Данный подход оправдан в тех случаях, когда априорные сведения об объекте весьма ограничены и когда реальная система настолько сложна, что, даже располагая информацией о состоянии ее элементов, практически невозможно связать эту информацию с общим поведением системы в целом.

Однако для реальных промышленных объектов химической технологии, как правило, характерно наличие априорной информации о внутренней структуре процессов, протекающих в них. При этом связь между поведением всей системы в целом и составляющих элементов можно установить либо на основе общих методов механики сплошной среды, либо на основе блочного принципа построения модели системы, исходя из набора элементарных типовых операторов. Поэтому изложенный здесь первый подход к синтезу функционального оператора ФХС, рассматриваемый как самостоятельный метод, обычно уступает по своей гибкости и эффективности второму и третьему подходам, о которых речь пойдет ниже. Вместе с тем очевидно, что в комплексном использовании и взаимном дополнении формальных и неформальных методов описания ФХС заложены большие возможности повышения эффективности решения проблемы синтеза функциональных операторов ФХС.