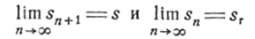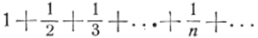Необходимый признак сходящегося ряда

Предполагая ряд (22) сходящимся, легко показать, что его общий член и_п стремится к нулю при неограниченном возрастании номера п. Действительно, так как последовательность чисел s_n сходится, то.

так как.

или, что-то же,

Итак, во всяком сходящемся ряде общий член стремится к нулю при неограниченном возрастании его номера п. Равенство (24) выражает необходимый признак сходимости бесконечного ряда; следовательно, в тех случаях, когда этот признак не выполняется, ряд расходится. Так, например, ряд 1 —{— ^ …

расходится при q^> 1, так как в этом случае его общий член qⁿ не стремится к нулю при неограниченном возрастании п: при |1 число qⁿ стремится к бесконечности, при | </1 = 1 модуль этого числа qⁿ всё время равен единице. В предыдущем пункте мы видели, что этот ряд есть собственно расходящийся, если |^|^>1; при |</| = = 1 этот ряд будет, вообще говоря, колеблющимся (за исключением q= 1, когда он собственно расходящийся), потому что в этом случае.

1 — О^п

сумма первых п его членов s_n = -j—— (q ф 1) не стремится к бесконечности при неограниченном возрастании п.

Установленный признак сходимости (24), будучи необходимым, не является достаточным, т. е. этот критерий может выполняться и в случае расходящегося ряда, как это показывает пример известного из анализа гармонического ряда.