Процессы течения расплавов полимеров в переходной зоне двухшиекового экструдера

Экспериментальные исследования на двухшнековых экструдерах с полимерами показали наличие между зонами пластикации (плавления) и дозирования (выдавливания) участков шнеков, винтовые каналы которых не полностью заполнены расплавом. Это объясняется тем, что объем С-образной секции винтового канала в зоне загрузки выполняется большим, чем в зоне дозирования, а удельный объем полимера по мере его… Читать ещё >
Процессы течения расплавов полимеров в переходной зоне двухшиекового экструдера (реферат, курсовая, диплом, контрольная)
Процессы течения расплавов полимеров в винтовых каналах и в зазорах зацепления двухшнековых экструдеров в настоящее время мало изучены, а в имеющихся публикациях авторы исходят из теории одношнековой экструзии или простых геометрических представлений. Недостаточность информации в этой области объясняется сложностью гидродинамических процессов, протекающих в двухшнековых экструдерах. Только с середины 70-х годов XX в. начали появляться теоретически обоснованные исследования в этой области.
При решении рассматриваемой задачи используются общепринятые допущения — несжимаемость жидкости, стационарность процесса, условия прилипаемости, пренебрежение инерционными и массовыми силами.
Для упрощения рассматривается изотермическая задача, жидкость принимается ньютоновской, а неньютоновский характер реальных полимеров учитывается использованием понятия эффективной (кажущейся) вязкости. При этом эффективную вязкость перерабатываемого материала необходимо определять по среднеинтегральной скорости сдвига, методика расчета которой изложена ниже.
Экспериментальные исследования на двухшнековых экструдерах с полимерами показали наличие между зонами пластикации (плавления) и дозирования (выдавливания) участков шнеков, винтовые каналы которых не полностью заполнены расплавом. Это объясняется тем, что объем С-образной секции винтового канала в зоне загрузки выполняется большим, чем в зоне дозирования, а удельный объем полимера по мере его плавления уменьшается. Сложность гидрои термодинамических процессов, протекающих в винтовых каналах и зазорах зацепления шнеков, затрудняет выбор такой геометрии шнеков, которая обеспечивала бы полное заполнение винтовых каналов на всей их длине (от зоны плавления до зоны дозирования).
В настоящее время за основу при выборе геометрических размеров шнеков берут коэффициент сжатия (отношение объемов С-образных секций в зонах загрузки и дозирования), определяемый экспериментально.
Выбранную степень сжатия обеспечивают применением секционных шнеков (ступенчатое изменение объемов С-образных секций), изменением глубины винтовых каналов или шага нарезки. Во многих случаях применяются шнеки без компрессии (сжатия). При любой из указанных конструкций шнеков трудно добиться, чтобы винтовые каналы их по всей длине зоны плавления полностью были заполнены расплавом полимера.
Участок шнеков с не полностью заполненными винтовыми каналами вносит существенный вклад в суммарное смесительное воздействие, производительность и мощность привода двухшнековых экструдеров. Следовательно, учет этой зоны при анализе работы двухшнековых экструдеров необходим.
Модель течения расплава полимера в зоне прокатки двухшнековых экструдеров показана на рис. 2.53. Выражения для скоростей потока и давления в зоне прокатки можно получить решением уравнений движения и неразрывности.
Уравнение движения в этом случае с учетом принятых выше допущений принимает следующий вид:

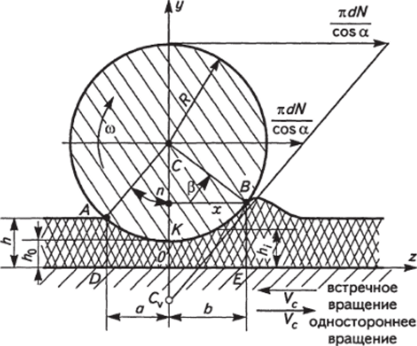
Рис. 2.53. Модель течения полимера в зоне прокатки двухшнекового экструдера.
Решение уравнения (2.95) при граничных условиях: для встречного вращения шнеков.
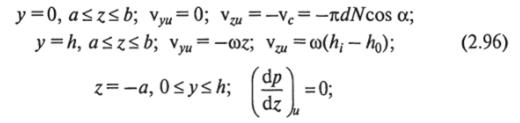
для одностороннего вращения шнеков.
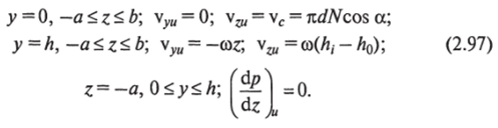
Для скоростей vOT получим следующие выражения: для встречного вращения шнеков.
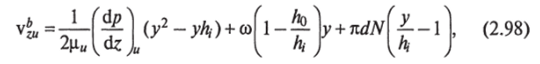
для одностороннего вращения шнеков.
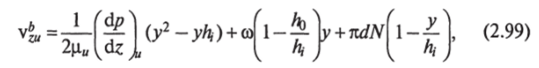
где (dp/dz)" — градиент давления в винтовом канале С-образной секции переходной зоны; ц" — эффективная вязкость расплава полимера; to —угловая скорость шнеков; d—диаметр сердечника шнека; N — частота вращения шнеков; А —глубина винтового канала.
Для нахождения градиента давления (d/?/dz)" обратимся к уравнению неразрывности, имеющему в рассматриваемом случае вид.

Беря от обеих частей этого уравнения интегралы по у в пределах от 0 до, А и принимая во внимание условия (2.96) и (2.97) для Чуй, получим выражение 
интегрированием которого по у находим:
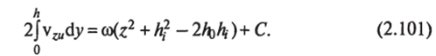
Совместным решением (2.98) и (2.101) с учетом последнего из граничных условий (2.96) определяем значение постоянной интегрирования С. 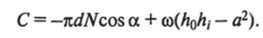
Градиент давления в переходной зоне.
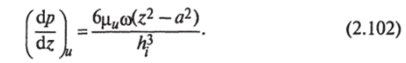
Текущее значение толщины h, является функцией координаты z- Из рис. 2.53 видно:
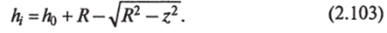
Тогда.
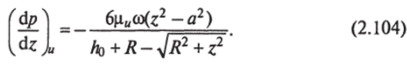
Нетрудно убедиться, что выражения для градиента давления (dp/dz) одинаковы для встречного одностороннего вращения шнеков. Величина (dp/dz) зависит только от угловой скорости <�в и эффективной вязкости ца, определяемой отдельно для встречного и одностороннего вращения шнеков.
Для нахождения вертикальной составляющей уи скорости потока в переходной зоне обратимся к уравнению неразрывности (2.100), откуда следует:
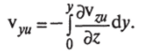
Тогда при встречном вращении шнеков.
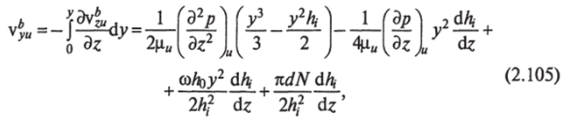
а при одностороннем вращении.
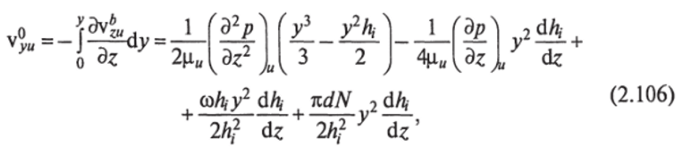
где ^ и «легко находятся из (2.103) и (2.104).
dz ydz2