Основные подходы к определению начальных значений

Рассмотрим три возможных подхода к определению начального значения базисного периода Т{) и соответствующих ему начальных коэффициентов кратности kx для каждой номенклатуры (этапы 2 и 3 вышеприведенного алгоритма).

Первый подход описан в работе Ю. И. Рыжикова^[1]. За основу начального значения периода группирования принимается период между независимыми поставками первой номенклатурной позиции, которой соответствует минимальная величина отношения Д²С_; / ДС_Х/. Тогда начальное приближение для базисного периода рассчитывается по формуле:

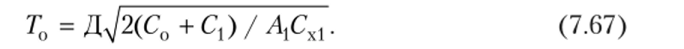
Базисному периоду соответствует коэффициент кратности k = 1. Для остальных позиций необходимо последовательно перебирать значения k_h начиная с 1 и продолжая до тех пор, пока выполняется условие.

Тогда наименьшее k_r при котором начинает не выполняться условие (7.68), и является начальным коэффициентом кратности для i-й позиции номенклатуры.

Второй подход описан в работе М. Харига¹. Выбор начального значения базисного периода Т₀ можно выполнить по множеству номенклатур, заказываемых в каждом периоде, при этом первые j-й номенклатурные позиции поставляются одновременно. В этом случае формула для расчета Т₀ будет иметь следующий вид:

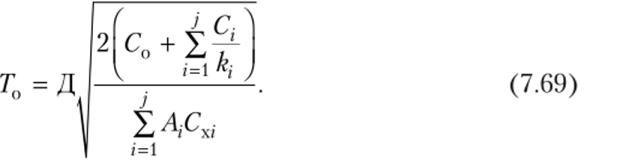
Присоединять к указанному множеству/ совместно заказываемых товаров следующие позиции окажется нецелесообразно в тот момент, когда будет выполняться следующее неравенство:

При подстановке (7.69) в формулу (7.70) получим условие прекращения накопления данного множества, имеющее вид неравенства:

/ .

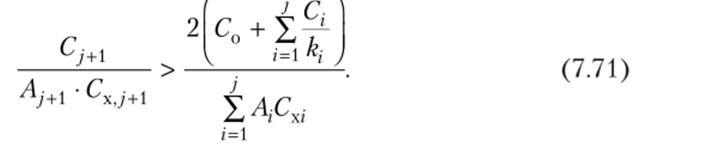
Проверка неравенств (7.70) и (7.71) начинается со второй позиции товарной номенклатуры, при этом в правой части неравенств подставляются значения С₀ + С, и А_хС_хХ. При выполнении условия (7.71) для j-й товарной позиции для всех последующих, для которых i > /, вычисляется оптимальный период между поставками Т_{ при независимых поставках и начальные значения коэффициентов кратности k_t но формуле.

¹ Ilariga М. Two new heuristic procedures for the joint replenishment algorithm //Journal of Operational Research Society. 1994. № 4. P. 463—471.

Третий подход представляет собой синтез первого и второго подходов^[2]. Начальное значение базисного периода принимается равным периодичности при независимых поставках первой позиции номенклатуры в ранжированном ряду на этапе 1 и рассчитывается по формуле (7.67).

Соответствующий базисному периоду набор коэффициентов, с помощью которых производится формирование базового варианта групп различной кратности, определяется по формуле (7.72).

? Разбор ситуации Пусть требуется выбрать наилучшую стратегию поставок из следующих вариан тов: 1) независимые поставки каждой позиции номенклатуры; 2) одновременная поставка всех номенклатурных позиций; 3) поставки по системе «кратных периодов».

В табл. 7.13 приведены данные о пяти видах продукции,/= 0,2.

Таблица 7.13

Исходные данные для выбора стратегии.

Сначала рассчитаем оптимальные параметры независимых поставок каждой номенклатурной позиции (табл. 7.14), а также отношение Д²С, / / AjC_xj, которое пригодится при расчетах для поставок по системе «кратных периодов».

Таблица 7.14

Результаты расчетов оптимальных параметров независимых поставок пяти номенклатур от одного поставщика.

Далее рассчитаем параметры одновременной многономенклатурной поставки пяти видов товаров:

• минимальные суммарные затраты:

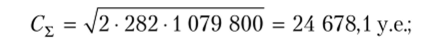
• величины размера заказа каждой номенклатуры по формуле (7.7):

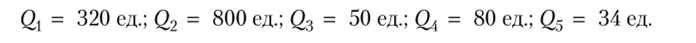
период между поставками:

количество поставок:

Теперь рассчитаем оптимальные параметры многономенклатурной поставки по системе «кратных периодов».

На первом этапе произведем ранжирование номенклатурных позиций по возрастанию предварительно рассчитанных отношений Д²С; / AjC_xi и произведем их перенумерацию (табл. 7.15).

Таблица 7.15

Ранжирование и перенумерация товарных позиций для системы «кратных периодов».

На втором и третьем этапе произведем выбор начального приближения для базисного периода Т₀ и определим соответствующие ему начальные коэффициенты кратности k_i для каждой номенклатуры. Выполним расчеты с помощью трех известных подходов.

Согласно первому подходу в качестве начального значения периода группирования принимаем период между независимыми поставками для первой номенклатуры из ранжированного ряда, рассчитываемый по формуле (7.67):

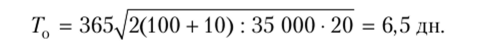
Таким образом, для первой номенклатуры коэффициент кратности равен k = 1. Теперь для каждой из оставшихся позиций будем последовательно перебирать значения k_v начиная с 1, до тех пор, пока выполняется условие (7.68). Наименьшие k_v при которых начинает не выполняться условие (7.68), и будут являться начальными коэффициентом кратности для каждой i-й позиции номенклатуры.

Пусть для второй позиции k₂ = 1, проверим выполнение условия (7.68):

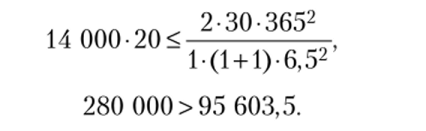
Условие (7.68) не выполняется — это означает, что необходимо принять k₂ = 1 в качестве начального коэффициента кратности для второй номенклатурной позиции.

Выполним ту же проверку для третьей позиции. Пусть k_s= 1, проверим выполнение условия:

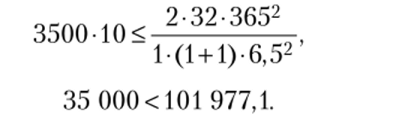
Так как условие (7.68) выполняется, необходимо продолжить поиск начального значения коэффициента кратности для данной позиции. Примем, что = 2, проверим выполнение условия:

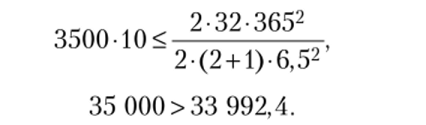
Таким образом, k₃= 2 — наименьшее значение среди коэффициентов кратности, при котором для третьей позиции перестает выполняться условие (7.68), примем его в качестве начального значения.

Аналогичным образом найдем начальные значения коэффициентов кратности для остальных номенклатур. В результате проверки начальные коэффициенты кратности для четвертой и пятой позиций оказались соответственно равны k_A = 3 и k₅ = 4.

Согласно второму подходу выбор начального базисного периода Т_п осуществляется по множеству товарных позиций, заказываемых в каждом периоде, при этом первые j позиции заказываются одновременно. На первом этапе задача сводится к определению количества таких позиций. Изначально первая номенклатура поставляется независимо, т. е.у = 1. Проверим, стоит ли поставлять вторую позицию одновременно с первой, для этого проверим выполнение условия (7.71):

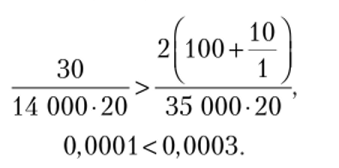
Так как условие (7.71) не выполняется, необходимо включить вторую позицию в группу позиций, поставляемых одновременно с первой.

Теперь проверим, стоит ли поставлять третью позицию одновременно с первыми двумя, для этого проверим выполнение условия прекращения накопления группы (7.71):

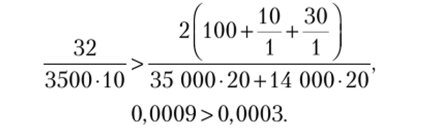
Так как условие выполняется, следует прекратить накопление группы, и третью позицию не поставлять одновременно с первыми двумя.

Таким образом, начальное значение базисного периода Г₀, соответствующее одновременной поставке двух номенклатур, т. е. для j = 2, a k_x — k₂ = 1, может быть рассчитано с помощью формулы (7.69):

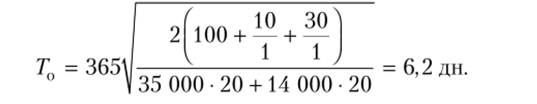
Далее для всех номенклатур, поставляемых отдельно от первых двух, рассчитаем начальные значения коэффициентов кратности по формуле (7.72):

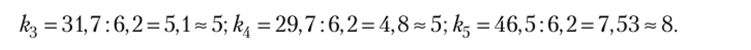
Согласно третьему подходу начальное значение периода группирования принимается равным периоду между независимыми поставками первой позиции номенклатуры в ранжированном ряду на этапе 1 и равно Т₀ = 6,5 дн.

Найдем набор начальных значений коэффициентов, соответствующих базисному периоду, по формуле (7.72):

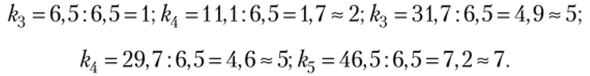
Представим результаты вычислений, полученных на втором и третьем этапах алгоритма с помощью трех способов расчета, в виде табл. 7.16.

Таблица 7.16

Результаты расчета начального значения базисного периода Т₀ и начальных коэффициентов кратности k_i

На четвертом этапе алгоритма рассчитаем вспомогательные параметры Р₀ и Р₁ с помощью формул (7.53) и (7.54). Далее для полученных коэффициентов, но формулам (7.52) и (7.55) вычислим оптимальный базисный период Г* и оптимальные затраты С*_ъ.

Проведем подробные вычисления для базового варианта групп различной кратности, полученного с помощью первого подхода:

Результаты вычислений вспомогательных параметров, а также оптимального периода группирования и суммарных затрат на управление запасами для базового варианта групп различной кратности приведены в табл. 7.17.

Таблица 7.17

Результаты расчета вспомогательных параметров (3₀ и р₄, оптимального базисного периода V и оптимальных затрат.

Поскольку наименьшие затраты на управление запасами были получены с помощью первого способа определения базового варианта групп различной кратности, то именно для него и будем в дальнейшем выполнять все оставшиеся этапы алгоритма.

Таким образом, базовый вариант предполагает, что первый и второй вид продукции поставляются одновременно с базисной периодичностью Т* (к_Л = k₂= 1), в то время как остальные позиции поставляются с периодичностями, кратными базисному периоду k{T*, при этом ?₃ = 2, k_A = 3, k₅ = 4. Для того чтобы найти оптимальную конфигурацию группировок номенклатурных позиций, перейдем к пятому этапу алгоритма и рассчитаем для каждой позиции левые и правые границы интервала постоянства группировок — Т_Я1 и Г_ш — по формулам (7.58) и (7.59).

Например, для первой позиции эти границы будут равны:

Рассчитанные границы для остальных товарных позиций приведены в табл. 7.18.

Таблица 7.18

Результаты расчета левых и правых границ интервала постоянства группировок — T_JU и Т_ш

По табл. 7.18 проверяем выполнение условия (7.60). Для первой, второй и четвертой позиций выполняется данное условие, т. е. оптимальный базисный период Т* находится между левой и правой границами интервала постоянства группировок. Что касается третьей и пятой позиций, для них данное условие оказалось нарушено, соответственно, группы кратности для этих позиций определены неверно.

На шестом этапе выявляем все номенклатурные позиции, для которых Т_Я1 > Т*_у в нашем случае речь идет о третьей и пятой номенклатурах.

Для каждой такой номенклатуры рассчитаем приращения величин Р₀ и Pj при переходе i-й номенклатуры из группы с кратностью k_t в группу с кратностью k_i + 1 но формулам (7.61) и (7.62):

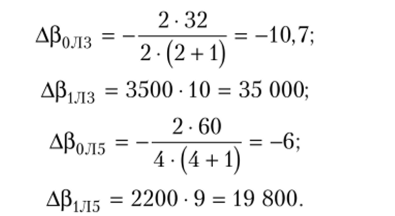
Далее найдем сумму приращений величин Р₀ и для всех выявленных номенклатур. В данном случае они будут равны:

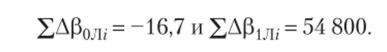
Заменим для третьей и пятой позиций k_t на k_t + 1, тогда k₃ = 3, k₅ = 5, и рассчитаем новые левые границы интервала постоянства группировок Т_ш по формуле (7.58). Новые левые границы для третьей и пятой номенклатур соответственно равны:

Далее вычислим новые значения (3₀' и (3/ но формулам (7.63) и (7.64):

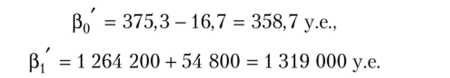
Для новых значений Р₀' и (3/ пересчитаем оптимальный базисный период Т* и оптимальные затраты С*_ъ по формулам (7.52) и (7.55).

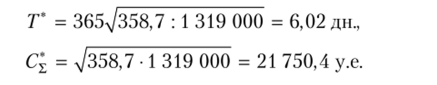
Таким образом, новая конфигурация группировок номенклатурных позиций предполагает, что они поставляются со следующими коэффициентами кратности: k_x — 1, k₂ = 1, k₃= 3, k_A = 3, k₅ = 5.

Рассчитаем для третьей и пятой позиции правую границу постоянства группировок по формуле (7.59). Границы интервала постоянства группировок с учетом откорректированных для третьей и пятой номенклатур представим в табл. 7.19.

Таблица 7.19

Результаты расчета левых и правых границ интервала постоянства группировок — Т_Л; и Г_ш — для новой конфигурации группировок номенклатур

Выполним новый поиск номенклатур, для которых не соблюдается левая часть неравенства (7.60), т. е. T_JU > Т*. Так как такие позиции отсутствуют, то переходим к следующему этапу алгоритма.

На этапе 7 алгоритма проверяем, есть ли номенклатуры, для которых 7'_{П (} < Т*. Анализ табл. 7.19 показал, что такие номенклатуры также отсутствуют.

Переходим к 8 этапу. Повторная проверка условия (7.60) показала, что оптимальный базисный период Т* = 6,02 дн. для всех номенклатурных позиций попадает в соответствующие интервалы постоянства группировок. Это означает, что для всех номенклатур группы кратности определены верно и найденная конфигурация группировок оптимальна. После восстановления первоначальной нумерации оптимальная конфигурация группировок будет включать в себя поставки номенклатур с коэффициентами кратности k_x = 1, k₂ = 1, &з = 5, k₄ = 3, k₅ = 3.

Анализ затрат на управление запасами при всех вариантах поставок показал, что при поставке по системе «кратных периодов» достигаются наименьшие затраты по сравнению с независимыми поставками каждой номенклатуры и одновременной поставкой всех номенклатур, о чем свидетельствуют данные табл. 7.20.

Таблица 7.20

Затраты на управление запасами при различных вариантах поставок пяти номенклатур от одного поставщика.

На рис. 7.2 отражены различные варианты поставок пяти номенклатур от одного поставщика.

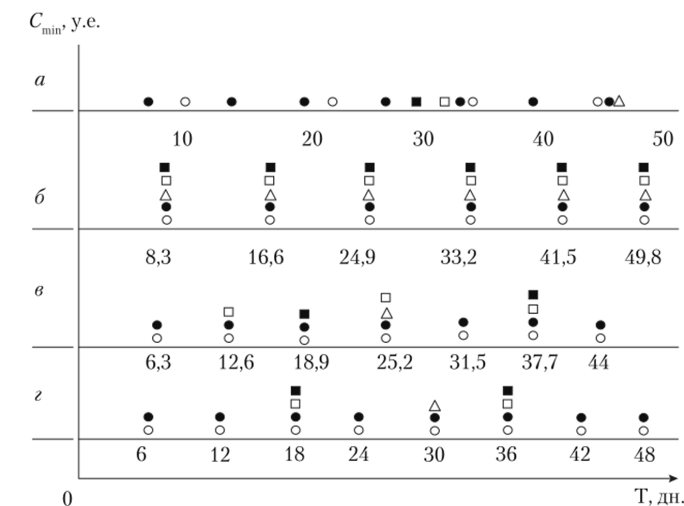
Рис. 7.2. Различные варианты многономенклатурных поставок:

а — независимая поставка (C_min= 27 655,9 у.е.); б — одновременная поставка (C_min = 24 678,1 у.е.); в — кратная поставка, базовый вариант (C_min = 21 782,9 у.е.); г — кратная поставка, оптимальный вариант (C_min = 21 750,4 у.е.); о — 1-й вид продукции; • — 2-й вид продукции; Л — 3-й вид продукции;? — 4-й вид продукции;? — 5-й вид продукции Для расчета размера заказа каждого вида продукции по системе «кратных периодов» воспользуемся формулой (7.56). Для продукции первого вида находим:

Соответственно, для остальных товаров получим 0₉ = 577 ед., = = 181 ед., Q./j = 173 ед., Q₅= 74 ед.

Таким образом, полученное решение является наилучшей стратегией поставок для рассматриваемых начальных условий. ?

• [1] Рыжиков Ю. И. Логистика, очереди и управление запасами: учеб, пособие /Ю. И. Рыжиков. СПб.: Изд-во ГУАП, 2011.
• [2] Модели и методы теории логистики / под ред. В. С. Лукинского. 2-е изд.