Анализ цепей с использованием функциональных рядов

Об использовании функциональных рядов в нелинейных цепях. Для анализа нелинейных цепей широкое применение находят функциональные ряды Вольтерра (ФРВ).

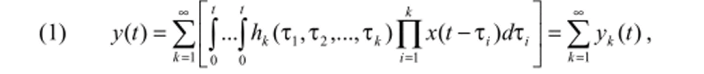
где А*(Ть т₂,…, т*) — ядро Вольтерра к-го порядка [12].

Класс электрических цепей, в котором используются ФРВ, называется классом Вольтерра — Винера, так как Н. Винер был одним из первых исследователей, который применил их для анализа цепей.

Характерные особенности цепей этого класса:

=> существование явной связи между воздействием и откликом;

=> одновременный учет нелинейных и инерционных (динамических) свойств цепи;

=> простые возможности перехода к описанию цепи для частных случаев:

t

• для линейной цепи к интегралу свертки: у = J A, (t).v (/ - т) dx;

о.

• для безынерционной цепи к степенному ряду у =hX + h₂ х² +…, который получается после подстановки Ai (Tj) = A|5(Ti); Л₂(Т|, т₂)= ⁼A₂S (t,)8(t₂); … в (1);

=> возможность блочного представления (рис. 1 _уа) отклика (1), что может значительно упростить задачу анализа для конкретных воздействий как по уровню, так и частотным свойствам и облегчить задачу выделения интересующих продуктов нелинейного преобразования. Использование блочной конструкции в виде последовательного соединения нелинейной и линейной цепей (рис. 1,6,в) позволяет при аппроксимации характеристики нелинейной цепи степенным полино- к

мом F (z) = 5>*z* представить отклики в следующем виде:

к

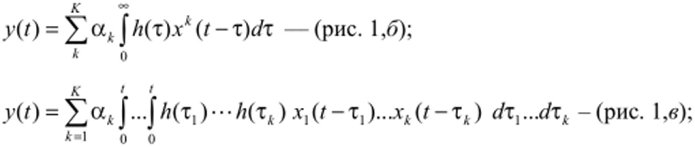
=> возможность перехода от оператора во временной форме (1) к оператору в частотной форме (см. и. 7.6) и обратно с помощью преобразований Лапласа (или Фурье), что облегчает задачу исследования сложных электрических цепей на основе частотных методов;

=> возможность представления системы нелинейных дифференциальных уравнений, записанной с использованием ФРВ, в виде линейных подсистем относительно ядер соответствующих порядков [24], что позволяет использовать эффективные методы анализа линейных цепей.

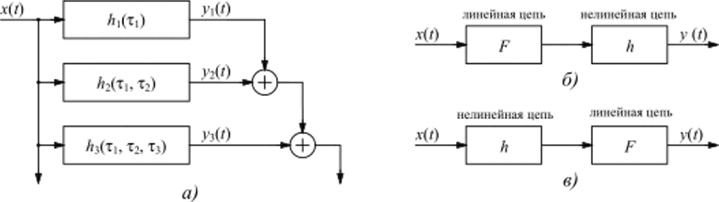
Рис. 1. Блочное представление электрической цепи.

В настоящее время разработано большое количество методов анализа цепей на основе ФРВ, которые относят к группе спектральных методов анализа и разделяют на методы малого параметра (методы символьного анализа, нелинейных токов, степенного ряда, многомерных рядов Маклорена) и методы последовательных приближений с использованием рядов Вольтерра — Пикара [1, 11, 12, 24].

Помимо анализа представление отклика нелинейной цепи в виде ФРВ позволяет также решить задачи идентификации, синтеза и оптимизации [12].

Известны методы, идеологически нс отличающиеся от ФРВ. К ним относятся метод анализа нелинейных многополюсников, метод нелинейного тока, метод многомерных рядов Маклорена, рядов Вольтерра — Пикара и др. Следует выделить метод многомерных рядов Маклорена, для которого разработаны высокоэффективные алгоритмы, позволяющие вычислять ядра Вольтерра высоких (/? > 3) порядков при многочастотном воздействии. Их применяют для анализа преобразователей частоты, детекторов и автогенераторов. Имеется ряд модификаций метода ФРВ для повышения эффективности при проведении численных расчетов.

К необходимым условиям использования ФРВ для анализа нелинейных цепей относят:

=> непрерывность и дифференцируемость оператора передачи цепи, однозначность связи «вход-выход»;

=> возможность разложения характеристик нелинейных компонентов цепи вблизи исходной рабочей точки в ряд Тейлора. Это условие равносильно требованию ограничения амплитуды воздействия, что соответствует слабо нелинейному режиму работы цепи;

=> существование устойчивого решения;

=> единственность решения системы уравнений цепи на постоянном токе;

=> отсутствие самовозбуждения при отключенном воздействии и нулевых начальных условиях, т. е. при х(/) = 0 цепь должна находится в состоянии устойчивого равновесия y (t) = 0.

Системы, для которых справедливо описание на основе ФРВ, называют аналитическими. К их основным фундаментальным свойствам относят физическую осуществимость и устойчивость [24].

Для проведения анализа нелинейной цепи с использованием ФРВ необходимо располагать выражениями ядер Вольтерра. В том случае, когда исходными данными служат схема или уравнения цепи, существуют методики [12], позволяющие найти точные аналитические выражения для ядер Вольтерра теоретически любого порядка. Если же параметры цепи известны приближенно или вообще неизвестны либо уравнения цепи слишком сложны, то применяют экспериментальные способы определения ядер Вольтерра.

При проведении анализа должна быть уверенность в том, что при заданном внешнем воздействии ряд (1) сходится. Поскольку вычисление ядер сопряжено с известными трудностями, представляют интерес оценки радиуса сходимости ряда (1) для заданной цепи. Для некоторых классов цепей такие оценки приведены в [12, 24]. Однако они не всегда удобны для практического использования и зачастую дают заниженные значения радиуса сходимости ряда. В инженерной практике распространен другой подход к решению вопроса сходимости и оценке погрешности, состоящий в последовательном расчете членов ряда (1) и сравнении каждого последующего члена с суммой предыдущих.

Стратегия формирования системы уравнений, построения отклика цепи для низких порядков (и = 1… 5) и ряд других вопросов описан в литературе [1, 11, 12, 24]. Рассмотрим некоторые методы, позволяющие установить связь между воздействием и откликом [1].

Метод примою разложении. Эгот метод состоит в таких преобразованиях исходных уравнений электрической цепи, в результате которых они принимают форму разложения в ряд Вольтерра (1). Затем с помощью л-кратного преобразования Фурье определяют ядра Вольтерра в частот;

ной области H_nZ, f₂,…, f_2n или передаточные функции. Связь между входным и выходным величинами в общем случае имеет вид.

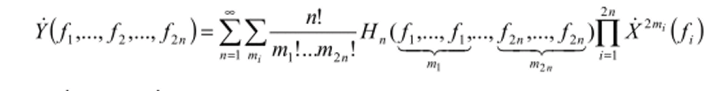
где X (f) и Y (J) — комплексные полуамплитуды спектральных составляющих сигналов на входе и выходе нелинейной системы; 2] означает суммирование по всем возможным наборам т, — х, отве;

щ

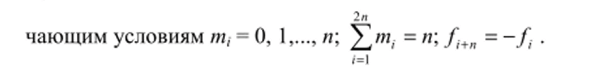
Метод испытательных сигналов. Его суть заключается в определении передаточной функции Вольтерра H"{fu •••> />) при входном воздействии.

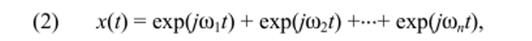
где (о, = 2nfi i = 1, 2,п, причем со, несоизмеримы.

Пусть нелинейная цепь:

=> содержит нелинейное сопротивление с вольт-амперной характеристикой.

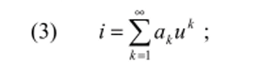
=> описывается уравнением.

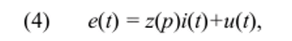
где e (t) — входной сигнал; i (t) и u (t) — соответственно ток через нелинейное сопротивление и напряжение на нем; p=d/dt — оператор дифференцирования.

При выбранных входном воздействии (2) и характеристике (3) ряд Вольтерра для напряжения на выходе нелинейной цепи u (t) будет иметь вид.

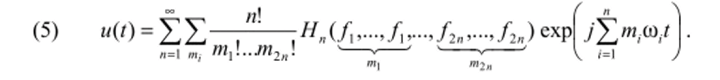
При использовании рассматриваемого метода передаточные функции Вольтерра определяются последовательно, но мере увеличения их порядка, поэтому сначала положим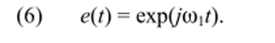

В этом случае в соответствии с (5).

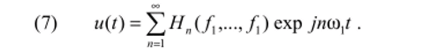
Подставив (7) в (4) с учетом (3) и (6), получим.

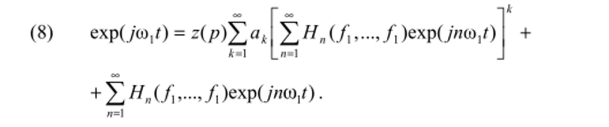
Приравняв коэффициенты в левой и правой частях (8) при схр (/0),/), получим 1 =tf|z (/(0|)-#i (/i) н- //|(/1), откуда находим.

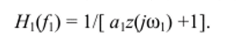
Для определения передаточной функции второго порядка H (f> f₂) принимаем e (t) = exp (/C0|f) + ехр (/'оы) и г. д. Продолжая подобные операции, можно вычислить передаточные функции любого порядка.

Сложность вычислений с ростом п резко увеличивается. Поэтому метод испытательных сигналов обычно применяют для определения передаточных функций первых порядков (/? < 4). Следует отметить, что метод пригоден только для получения аналитических выражений для, /,) — ^и его нельзя непосредственно использовать для экспериментального определения и для расчета с помощью ЭВМ передаточных функций общего вида. 'Эго связано с тем, ч то воздействие (2) не являемся действительным числом.

Метод нелинейных генераторов. В основе этого метода лежит последовательное определение выходных реакций>"(/) (1) для п= 1, 2, 3,… Для пояснения его особенностей рассмотрим нелинейную цепь, описываемую дифференциальным уравнением (4). Допустим, что при воздействии на нее входного сигнала е(/) выходная реакция порядка п имеет вид u"(t). Тогда при подаче на вход сигнала e_E(t) =Ee (t) выходную реакцию /?-го порядка можно представить как u_E«(t) =E?u_n(t) [1], где Е — фиктивная переменная, введение которой существенно упрощает решение поставленной задачи.

После подстановки e_E(t) и u_En(t) в (4) получим.

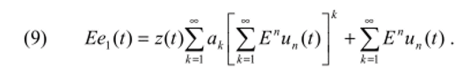
Для определения U (t) продифференцируем обе части (9) по Е, а затем примем Е= 0, тогда.

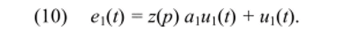
Таким образом, реакция первого порядка u (t) отыскивается в результате решения линейного дифференциального уравнения (10), которое описывает исходную цепь, если в ней вместо нелинейного сопротивления (2) включить линейную проводимость, равную а.

Для определения реакции второго порядка u₂(t) дважды продифференцируем (9) по ?, после чего, приняв Е = 0, получим.

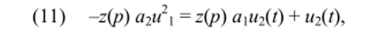
где М|(/) — решение уравнения (10).

Описанная процедура повторяется до тех пор, пока не будут рассчитаны все выходные реакции u (t), 112(f)"" ' u_n(t). Затем, применяя к найденному отклику !#(/) = Ъ (_п(0 преобразование Фурье, определяется спектральный состав выходного сигнала.

Таким образом, для определения реакции u_k(t) k-vo порядка каждый раз необходимо решать линейное дифференциальное уравнение, описывающее исходную цепь, в которой источник входного сигнала заменен нелинейным генератором. При этом ЭДС генератора выражается через выходные реакции более низкого порядка.

В общем случае ЭДС нелинейного генератора для расчета выходной реакции я-го порядка.

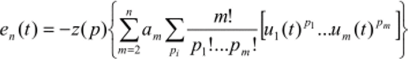
где Хр, означает, что суммирование производится по всем наборамр, р_ъ …, р_т, удовлетворяющим условиям.

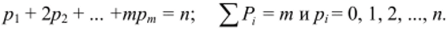
Определение выходных реакций различных порядков можно упростить, если первое слагаемое в характеристике (3), отражающее линейную зависимость между /(/) и м (/), отнести к линейной части схемы.

При анализе нелинейных цепей общего вида на каждом шаге, позволяющем рассчитать выходную реакцию последующего порядка, приходится решать не одно линейное дифференциальное уравнение, а систему.

Таким образом, выходную реакцию нелинейной цепи методом нелинейных генераторов находят, многократно решая линейное дифференциальное уравнение вида (10) при различных значениях левой части.

Наиболее трудоемким этапом анализа нелинейных систем с применением аппарата функциональных рядов Вольтерра является определение.

передаточных функций или выходных реакций соответствующего порядка. Если же эти характеристики известны, то отыскать выходной отклик при заданном входном воздействии не составляет труда. Отметим, что после отыскания выходных реакций требуемого порядка можно не определять передаточные функции Вольтерра, так как разложение u (t) в ряде Фурье позволит сразу оценить его спектральный состав.