Формирование ММС в базисе узловых напряжений

Общее представление ММС. В базисе узловых напряжений исходные уравнения (1) можно представить в виде [15].

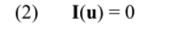
и для расчета схемы при использовании метода Ньютона сформировать алгоритм.

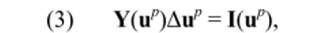
где I (u) — вектор узловых токов; Y = [Э1/Эи] — матрица узловых проводимостей; р — индекс ньютоновских итераций; Ди⁷' = и⁷*¹ — и⁷' — вектор поправок.

Представим ММС (3) для схемы, содержащей п узлов, в матричной форме.

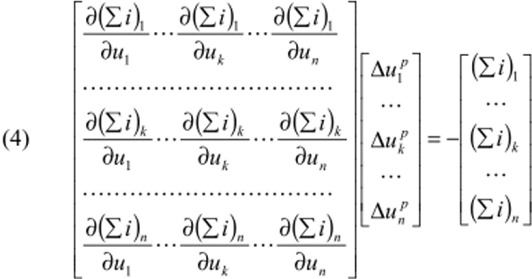
где / = /(и 1,и_к,и") — ток ветви или полюсный ток многополюсника; (Z/)y, у = 1,… к, …, п — узловой току-го узла, т. е. алгебраическая сумма токов компонентов схемы, соединенных в у-м узле (инцидентных у-му Э (1″).

узлу); —— —собственная (при у = к) или взаимная (при у Ф к) узловая.

ди_к

проводимость Yjk между узлами у и к.

Статический режим. При формировании (4) последовательно рассматривается каждый компонент схемы и определяется его вклад в вектор узловых токов 1(и) и матрицу Y узловых проводимостей.

Формирование вектора узловых токов I (u) состоит в образовании для каждого узла схемы суммы полюсных токов компонентов, соединенных с этим узлом. При этом обычно ток, втекающий в узел, входит в узловой ток этого узла со знаком «-», а вытекающий — со знаком «+». Например, ток двухполюсника / = f (и_г—м,), включенного между узлами г и /, направленный от узла г к узлу /, будет участвовать в формировании г-го компонента I, вектора узловых токов I в качестве слагаемого со знаком «+» иу-го компонента /у — со знаком «-».

Формирование матрицы узловых проводимостей Y. Для /г-полюсника, каждый полюсный ток /* которого непосредственно зависит от потенциа;

лов всех остальных полюсов, т. е. /* = /*(wi, м*, и_п), матрица полюсных проводимостей многополюсника.

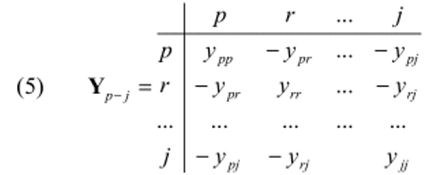
где р, г, …, j— номера полюсов многополюсника в схеме; урр, у_гп — собственные проводимости полюсов р, г, …J, равные суммам проводимостей л-полюсника, инцидентных полюсамр, г, …J соответственно;^, у_Рр … — взаимные проводимости между полюсами л-полюсника.

При формировании матрицы Y (u) дл я всей схемы используется метод позиционного суммирования [15], согласно которому => элемент Уц матрицы Y (u) получается суммированием всех проводимостей схемы, включенных между узлами / и к. При этом также учитывается взаимная проводимость у,*, которая входит в состав матрицы Ypj л-полюсника, если / и к являются его полюсами;

=> в состав элемента У" матрицы Y (u) входит в виде слагаемого собственная проводимость уа л-полюсника, когда /-й узел схемы одновременно является полюсом л-полюсника.

На основании изложенного, можно построить следующий алгоритм формирования М М С [ 15]:

Шаг 1. Уравнение каждого элемента схемы представляется в виде i, = = Y., u+I" где Y" 1_э — матрица полюсных проводимостей элемента и вектор полюсных токов;

Шаг 2. Выделяются и обнуляются двумерные или одномерные массивы для записи в них матрицы узловых проводимостей схемы Y и вектора узловых токов I, являющихся основными компонентами ММС.

Шаг 3. Рассматривается очередной А'-й элемент схемы. Компоненты его вектора I, и матрицы Y, заносятся на соответствующие позиции массивов I, Y и суммируются с их содержимым.

Шаг 4. Если список элементов нс исчерпан, то повторяется п. 3, если исчерпан, то формирование ММС на этом заканчивается.

Динамический режим. При формировании ММС для расчета переходных процессов в составе вектора I (u) и магрицы Y (u) нужно учесть уравнения емкости /_с = Cdu^dt и индуктивности u_L = Ldirfdt. Для этого уравнения дискретизируют на заданном (выбранном) интервале At

по формулам численного дифференцирования или интегрирования и представляют в виде.

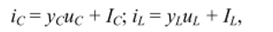
где у о Уь ^ul — проводимости и напряжения реактивных ветвей; /_с, I_L —.

источники тока.

Если уравнения электрического равновесия составляются для точки то при использовании неявных численных методов решения дифференциальных уравнений получают алгоритмы вида.

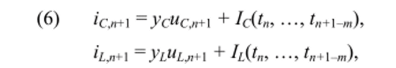
а при использовании явных методов — вида.

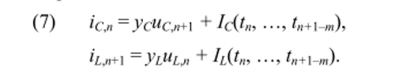
Конкретная форма представления (6), (7) зависит от выбранного метода численного интегрирования дифференциальных уравнений (Эйлера, трапеций, ФДН и др.).