Статически определимые и статически неопределимые системы

Система называется статически определимой, если число неизвестных в ней равно числу полезных уравнений равновесия. Для всякой пространственной системы сил (рис. 1.12, я) можно составить.

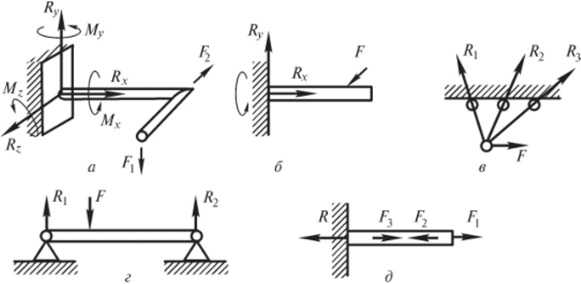
Рис. 1.12. Различные системы сил систему из шести уравнений равновесия и, решив ее, найти шесть неизвестных сил. Однако среди этих уравнений могут быть тождества, обрашаюшиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил должно быть равно числу уравнений минус число тождеств.

Для произвольной плоской системы сил (рис. 1.12, б) можно составить три уравнения, не являющихся тождествами, например сумму проекций всех сил на две любые оси и одну сумму моментов всех сил, относительно какой-либо точки.

Для плоской системы сходящихся сил (рис. 1.12, .

Для плоской системы параллельных сил (рис. 1.12, г) бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Соответственно из двух любых уравнений равновесия можно найти лишь две неизвестные силы.

Для системы коллинеарных сил (действующих вдоль одной прямой линии) (рис. 1.12, д) можно составить лишь одно полезное уравнение — сумму проекций всех сил на эту прямую, которая равна сумме сил.

Система называется статически неопределимой, если число неизвестных в ней больше числа полезных уравнений равновесия. Степень статической неопределимости равна разности между числом неизвестных и числом полезных уравнений равновесия (не являющихся тождествами). Для раскрытия статической неопределимости существуют разные способы, которые будут рассмотрены далее. Заметим лишь, что всякая реакция возникает в местах наложения внешних связей (ограничений движения системы): нет ограничения — нет реакции, есть ограничение — есть реакция. В то же время любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений. В результате появляется возможность сделать число уравнений равным числу неизвестных и решить систему уравнений.

На рис. 1.13, я показана система, когда стержень недостаточно закреплен, он может свободно вращаться под действием силы. Это — механизм. Такие задачи требуют учета сил инерции и рассматриваются в курсе теории машин и механизмов. Система из двух стержней (рис. 1.13, б) — статически определимая: два усилия в двух стержнях определяются из двух уравнений равновесия. Система из трех стсржней (рис. 1.13, в) — один раз статически неопределима: неизвестных усилий — три, полезных уравнений равновесия — два, степень статической неопределимости 3 — 2 = 1.

Рис. 1.13. Статически определимые и статически неопределимые системы.

На рис. 1.13, г показана система, три раза статически неопределима: неизвестных усилий — пять, полезных уравнений равновесия — два, степень статической неопределимости 5 — 2 = 3.

При большом количестве опор и шарниров определить степень статической неопределимости довольно трудно. Проще это сделать следующим образом. Мысленно отбросьте связи по одной до тех пор, пока система не превратится в механизм. Верните на место одну связь (любую). Система станет статически определимой. В таком виде число отброшенных связей равно степени статической неопределимости системы.

Решение статически неопределимых задач — значительно более сложная и трудоемкая проблема. Практически без использования компьютера можно решить лишь 2—3 раза статически неопределимые задачи. С использованием Mathcad можно решить задачи с большой степенью статической неопределимости.