Вращающееся магнитное поле

Как уже отмечалось, одной из основных причин широкого распространения трехфазной системы токов является возможность получения с ее помощью вращающегося магнитного поля, которое используется для создания асинхронных и синхронных двигателей.

Впервые вращающееся магнитное поле, возбужденное трехфазной системой токов, было применено выдающимся русским.

Рис. 5.9.4.

электротехником М.О.Доливо-Добровольским в 1889 г. при создании простейшего по устройству и надежного в эксплуатации асинхронного трехфазного двигателя.

Под вращающимся магнитным полем понимают постоянный по величине магнитный поток, вращающийся в пространстве с постоянной угловой скоростью. Такое поле можно получить, например, при вращении постоянного магнита вокруг оси, перпендикулярной линиям индукции, или внутри системы трех катушек, плоскости которых повернуты на угол 120° и которые питаются токами, смещенными во времени на 1/3 периода.

При симметричном исполнении катушек (одинаковое число витков, намотанных одним и тем же проводом на одинаковых сердечниках) амплитуды намагничивающих токов в них будут равны друг другу:

Г рафики мгновенных значений токов i_A, /_я, i_c даны на рисунке 5.10.1, а.

Рис. 5.10. l, a

Каждая из катушек в центре создает свою составляющую суммарного магнитного поля, индукция которого пропорциональна току и направлена по оси катушки (см. рис. 5.10.16). Вследствие этого мгновенные значения магнитных индукций катушек описываются выражениями.

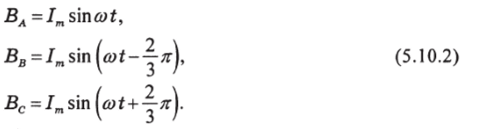
В общем центре мгновенные индукции катушек, складываясь создают магнитную индукцию результирующего поля.

Это поле удобно определять через составляющие по осям Хи Y.

Проведем координатные осиХи Yтак, чтобы ось Xсовпадала с геометрической осью катушки, А (см. рис. 5.10.1). Очевидно, что.

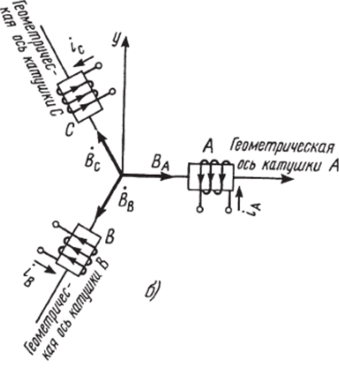
Рис. 5.10.10.

составляющая В_х вектора результирующей магнитной индукции на оси X равна сумме составляющих В^, В_хВ, В_хС, на ту же ось векторов магнитной индукции.

Из рисунка 5.10.1 имеем.

Подставляя в последнее уравнение значения магнитных индукций из уравнения (5.10.2) получим.

Аналогичным образом находим составляющую результирующего вектора магнитной индукции по оси У

Из рисунка 5.10.1 имеем.

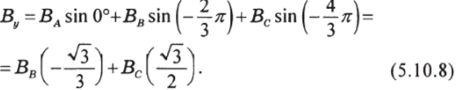
Подставляя в уравнение (5.10.8) значения магнитных индукций из уравнений (5.10.2) получим.

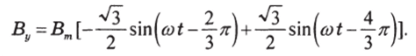
После упрощения получим.

По составляющим и находим значение суммарной магнитной индукции:

Уравнение (5.10.10) показывает, что результирующее поле постоянно по величине. Угол Д образованный вектором результирующей магнитной индукции с осью У (рис. 5.10.2),.

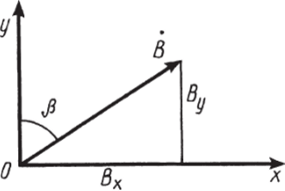
Рис. 5.10.2.

определится из условия

Из уравнения (5.10.11) следует, что направление вектора суммарной магнитной индукции непрерывно изменяется с течением времени, т. е. поле будет вращающимся. Угловая скорость вращения этого поля будет равна.

Таким образом, вектор суммарной магнитной индукции вращается в плоскости осей катушек с постоянной угловой скоростью Q = со, оставаясь постоянным по величине. Очевидно, что конец вектора магнитной индукции опишет окружность. Такое вращающееся поле называется круговым.

В асинхронных трехфазных двигателях для создания двухполюсного вращающегося магнитного поля три намагничивающие катушки (обмотки) располагаются на внутренней поверхности неподвижной части двигателя-статоре.

На рисунке 5.10.3 изображена схема размещения трех катушек.

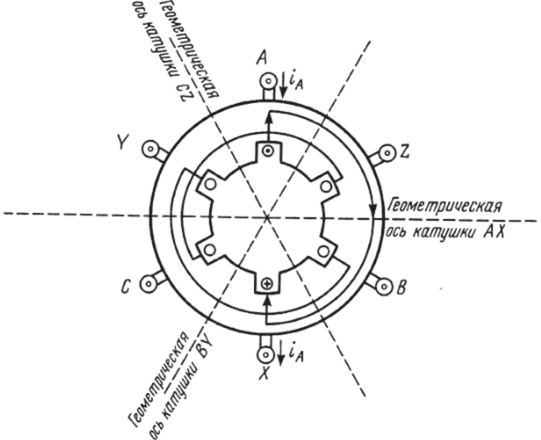
Рис. 5.10.3.

(С целью упрощения рисунка катушки изображены одновитковыми.)

Условимся считать ток в катушке положительным, когда он направлен от начала кату шки к ее концу, и отрицательным при обратном направлении (на рисунке 5.10.3 дано изображение положительного тока фазы АХ). В сечении витка фазы АХ крестиком и точкой изображено направление тока.

При подключении трехфазной системы напряжений возникает вращающееся магнитное поле. Картина результирующего поля непрерывно изменяется, но ее можно построить для любых фиксированных моментов времени в течение периода Т. Картина результирующего магнитного поля для момента времени /, когда ток в обмотке фазы АХ максимален и положителен i_A = /_ж > 0, показана на рисунке 5.10.4,а.

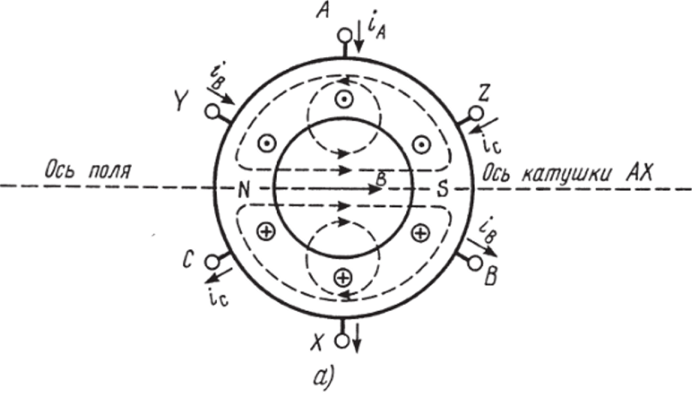
Рис. 5.10.4а

Для рассматриваемого момента времени токи в обмотках фаз BY и CZ отрицательные и равны половине максимального тока 1_т фазы АХ так как i_a + i_b + i_b = 0 в любой момент времени (см. рис. 5.10.1, я). Вследствие этого в рассматриваемый момент времени токи в обмотках фаз BY и CZ направлены от концов к их началам. Направление силовых линий магнитного поля, созданного группой проводников с одинаковым направлением тока в них, определено по правилу правоходового винта (буравчика).

Из рисунка 5.10.4,я видно, что в левой половине сердечника силовые линии направлены из стали в воздух, в правой — наоборот, следовательно, левая половина сердечника представляет северный полюс, а правая — южный. Ось суммарного поля совпадает с геометрической осью обмотки фазы АХ.

Выберем теперь другой момент времени: /₂, тогда ток в обмотке фазы BY максимален и положителен (i_B = 1_т > 0). Из рисунка 5.10.1, а следует, что в тот же момент времени токи в обмотках фаз АХ и CZ отрицательны и равны половине максимального тока 1_т. Повторив тот же метод построения упрощенной картины линий магнитной индукции суммарного поля, убеждаемся, что осьсуммарного поля повернулась на 120° и совпадает с осью обмотки фазы BY (рис. 5.10.4,6).

На рисунке 5.10.4,в показана упрощенная картина линий магнитной индукции суммарного поля для момента времени /₃, когда ток в обмогке фазы CZ положителен и максимален.

Рис. 5.10.4,?, 6

Из рисунка видно, что ось суммарного поля повернулась на угол 120° относительно оси обмотки фазы и совпадает с осью обмотки фазы CZ.

Анализируя картины магнитных полей, изображенных на рисунке 5.10.4, легко установить, что ось суммарного магнитного поля располагается по оси катушки той фазы, в которой ток максимален и вращается в направлении фаз с отстающим током. Если изменить порядок чередования фаз трехфазной сети с прямого на обратный, то и направление вращения суммарного поля изменится на противоположное.

Определим теперь скорость вращения двухполюсного вращающегося магнитного поля. Как следует из рисунка 5.10.4, а, б, в, ось двухполюсного вращающегося поля поворачивается на 360° (т.е. совершает один оборот) за время Т, равное периоду изменения тока. Очевидно, что за 1 мин (60 с) магнитное поле сделает п оборотов:

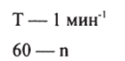
Составив соответствующую пропорцию, получим.

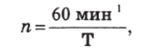
Учитывая, что /= 1/Т, найдем.

Двухполюсное поле вращается со скоростью, пропорциональной частоте изменения токов в обмотках фаз (катушках) статора. Следует обратить внимание на то, что вектор магнитной индукции результирующего магнитного потока совпадает с осью катушки той фазы, ток в которой имеет максимальное значение. Трехфазная система током может возбуждать в трехфазной обмотке статора не только двухполюсное, но и многополюсное вращающееся магнитное поле. Для этого необходимо количество катушек в фазе увеличить в число раз, равное числу полюсов магнитного поля, а угловые размеры катушек уменьшить во столько же раз. Так, для создания поля с двумя парами полюсов (р-2, четырехполюсное поле) в каждую фазу обмотки статора необходимо включить по две катушки, соединенных последовательно, а угловые размеры уменьшить в 2 раза, т. е. стороны витков уложить в пазы, расположенные под углом 180/2 = 90°, а оси катушек разных фаз расположить под углом 120/2 = 60°.

Схема расположения катушек четырехполюсной обмотки в пазах статора для фазы АХ приведена на рисунке 5.10.5. На рисунке 5.10.6 дана схема расположения катушек четырехполюсной обмотки в пазах статора.

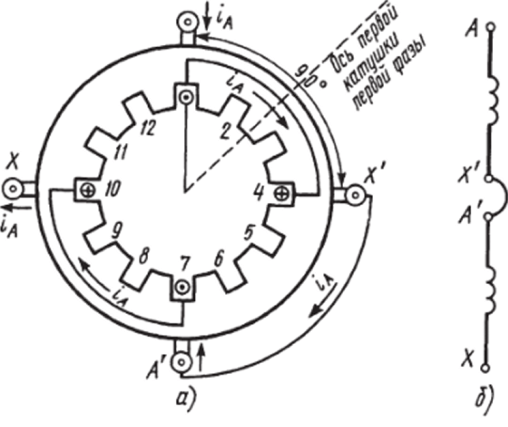
Рис. 5.10.5.

Рис. 5.10.6.

Для момента времени /" когда ток в фазе АХ достигает максимального значения (i_a = 1_т > 0) крестиками и точками указаны направления токов в сечениях витков катушек статора. Упрощенная картина четырехполюсного магнитного поля показана на рисунке 5.10.7,а.

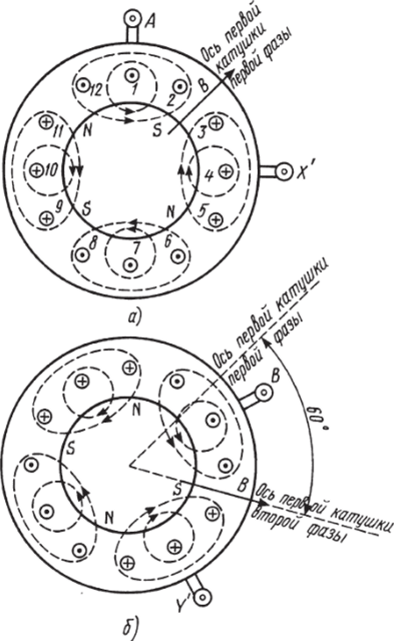
Рис. 5.10.7.

Построив аналогичным образом (рис. 5.10.7,в) упрощенную картину четырехполюсного магнитного поля для момента времени /₂, при котором ток в обмотке фазы BY достигает максимального значения (i_a = I_m> 0), нетрудно заключить, что вектор результирующего магнитного поля за время 1/3 периода повернулся на угол 60°. Следовательно, за время Т он повернется на угол 180°, т. е. на ½ оборота, а за 1 мин = 60 с.— п. Составив соответствующую пропорцию, получим.

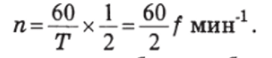
Если в статоре будет возбуждено шестиполюсное поле (/? = 3), то за один период изменения токов в катушках статора ось поля повернется на 1/3 оборота, при восьмиполюсном магнитном поле — на 1/ 4 оборота.

В справедливости сделанных выводов можно убедиться, построив соответствующие упрощенные картины магнитного поля для тех же самых выбранных моментов времени.

Поэтому скорость вращения магнитного поля относительно статора будет равна.

т.е. скорость вращения магнитного поля прямо пропорциональна частоте возбуждающих токов и обратно пропорциональна числу пар (р) полюсов.

При стандартной частоте (f= 50 Гц) скорость вращения магнитного поля в зависимости от числа образуемых им пар полюсов имеет значения, приведенные в таблице: