Что такое логика? Зачем ее изучать? Треугольник Фрегэ

Все три рассуждения построены по одной схеме: если первое, то второе; имеет место первое, значит, верно и второе. Сначала устанавливается связь между первым и вторым утверждениями, затем констатируется первое (приняты две посылки), тогда из этого с необходимостью вытекает второе. Это заключение вытекает с какой-то принудительной силой. Формальная логика изучает проблемы смысла и значения… Читать ещё >
Что такое логика? Зачем ее изучать? Треугольник Фрегэ (реферат, курсовая, диплом, контрольная)
Размышляя, мы всегда ощущаем определенное давление и несвободу: согласившись с одними утверждениями, мы вынуждены принять и другие, вытекающие из них, независимо от нашего отношения к ним. Если мы считаем, что каждая рыба плавает, мы вынуждены констатировать, что сова к рыбам не относится. Что является причиной этого принуждения? Какие законы лежат в основе нашего мышления?
Над этими вопросом человек задумался давно. Из подобных размышлений возникла наука логика.
Итак, логику можно определить как науку о законах и приемах правильного мышления. Но слово «логика» многозначно. Под логикой могут понимать определенную последовательность событий, поступков; логика может отражать свойства мышления, такие как определенность, последовательность, доказательность, и наконец, логика может рассматриваться как наука о мышлении[1].
По мнению Ж. Пиаже, логическое мышление — самый сильный интеллектуальный инструмент, который имеет человек для познания мира. Пока не будут сформированы умственные операции, человек не сможет понять то, что его окружает. Решение математиче;

Рис. 21.1.
ских задач в конце концов тоже сводится к логике, так как в решении каждой задачи используются различные высказывания или логические функции и операции над ними, а также и различные правила вывода, которые являются объектом изучения логики.
Американский психолог Д. Карнеги писал: «Разница между правильным и неправильным образом мыслей состоит в том, что правильный образ мыслей основан на анализе причин и следствий, он ведет к логическому конструктивному планированию; неправильный образ мыслей часто ведет к напряжению и нервным срывам»1.
Как же различать правильные и неправильные рассуждения?
Разобраться в этом нам помогут примеры. Первый из них был известен еще в Древней Греции.
- 1. Всякий человек — живое существо; Сократ — человек, значит, Сократ — живое существо.
- 2. Если человеку исполнилось 18 лет, то он может участвовать в выборах губернатора города; Дмитрию исполнилось 18 лет, значит, он будет участвовать в выборах губернатора.
- 3. Если Земля вращается вокруг своей оси, реки на ее поверхности подмывают один из своих берегов; Земля вращается вокруг своей оси, значит, реки на ее поверхности подмывают один из своих берегов.
Все три рассуждения построены по одной схеме: если первое, то второе; имеет место первое, значит, верно и второе. Сначала устанавливается связь между первым и вторым утверждениями, затем констатируется первое (приняты две посылки), тогда из этого с необходимостью вытекает второе. Это заключение вытекает с какой-то принудительной силой[2][3].
0 чем бы мы ни рассуждали таким образом, рассуждение остается правильным.
Попробуйте придумать свои примеры, предложив вместо первое и второе два конкретных утверждения.
Теперь давайте изменим схему так: если первое, то второе; имеет место второе, значит, верно и первое. Например: если у человека повышена температура, то он болен; человек болен, значит, у него повышена температура. Верно ли такое рассуждение?
Очевидно, что нет. Ведь человек может быть больным и без температуры.
Итак, характерной чертой правильного рассуждения является то, что оно от истинных утверждений (посылок) ведет также к истинной посылке (заключению). Если же хотя бы одна из посылок ложна, то заключение может быть как истинным, так и ложным.
Логику, таким образом, можно определить как науку о правильных рассуждениях. Причем правильность рассуждения определяется только формой этого рассуждения. Последнее утверждение является основным принципом логики, которую в связи с ним называют формальной.
Например, рассуждение, имеющее форму «если А, то Л», будет при истинных посылках давать истинное заключение независимо от содержания утверждений А и В.
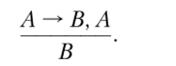
Формальная логика изучает проблемы смысла и значения выражений языка, различные отношения между понятиями, определение понятий, деление и классификацию, вероятностные и статистические рассуждения, доказательства, парадоксы, софизмы. Но главное — анализ правильности рассуждений, исследование «принудительной силы речи»[4].
Формальная логика, исследуя логическую форму, т. е. способ связи утверждений, анализирует и содержание, присутствующее в ней.
Рассмотрим два утверждения: «Все кошки черные» и «Треугольная пирамида имеет четыре грани».
Заменим содержательные компоненты утверждений буквами S и Р, не несущими никакого содержания. В итоге в обоих случаях получим «S есть Р». Это и есть логическая форма, полученная в результате отвлечения от конкретного содержания. S обозначает субъект утверждения (о чем утверждение), а Р — предикат (что говорится о субъекте).
Логический анализ мышления всегда имеет форму исследования языка, в котором он протекает и без которого он не является возможным. В этом плане логика — наука о мышлении — есть в равной мере наука о языке. Одна из особенностей искусственного языка состоит в строгой определенности его словаря, синтаксиса и семантики. В языке логики выделяют следующие категории.
Содержательные символы — выражения языка, имеющие содержание даже в том случае, если они взяты сами по себе. К ним относятся имена и высказывания. Имена обозначают какие-либо объекты, высказывания описывают или оценивают некоторые ситуации.
Логические символы — выражения языка, не имеющие самостоятельного содержания, но в сочетании с одним или несколькими выражениями образующие сложные выражения с самостоятельным содержанием. Из логических символов выделяют следующие:
- • логические связки, позволяющие из одних высказываний образовывать новые: и; или; если, то; неверно, что … и т. п.;
- • логические связки, позволяющие из двух имен получить высказывание: есть, все … есть, некоторые … есть; все … не есть; некоторые … нс есть.
Содержательные символы определяют содержание мысли, логические — ее логическую форму. Чтобы выявить логическую форму рассуждения, следует отвлечься от его содержания. С этой целью в логике принято заменять содержательные элементы знаками, не имеющими никакого содержания, а указывающими только вид заменяемого выражения. Этот искусственный язык пригоден только для одной цели — строгой формулировки логических законов (рис. 21.2).
Выражение языка — имя, если оно может использоваться в качестве подлежащего или сказуемого либо именной части сказуемого в простом предложении: «5 есть Р».
Например, из имен «Лобачевский» или «Менделеев» или «человек, создавший неевклидову геометрию» мы можем получить осмысленные предложения. Составьте их. Определите истинностные значения (истинно или ложно).
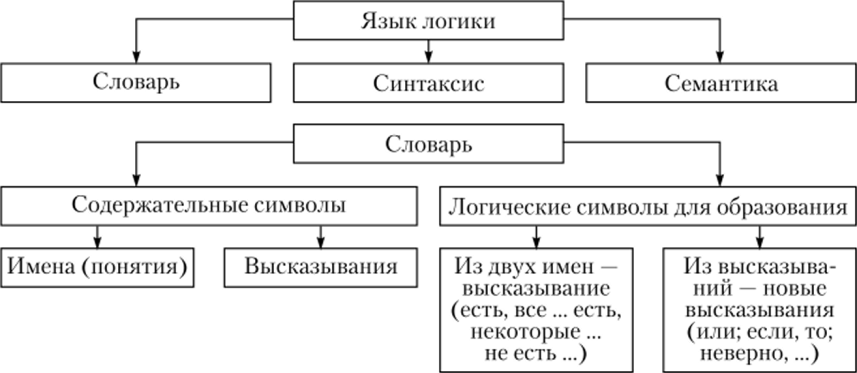
Рис. 21.2.
У вас должны получиться такие ответы. Лобачевский — человек, создавший неевклидову геометрию. Менделеев — человек, создавший неевклидову геометрию. Первое истинно. Второе ложно.
Употребление имен должно подчиняться следующим принципам.
- 1. Принцип однозначности: имя должно обозначать только один предмет, класс предметов или свойство. В естественном языке слова и выражения обычно многозначны. Поэтому этот принцип применительно к такому языку формулируется менее строго: в пределах одного контекста или одного рассуждения они должны быть однозначными, т. е. относиться к одним и тем же объектам.
- 2. Принцип предметности: всякое предложение должно говорить о предметах, обозначаемых входящими в него именами. Так, предложение «Москва — столица России» говорит не об именах «Москва» и «Россия», а о городе Москва и стране России.
Имена (понятия) различаются по количеству обозначаемых ими предметов. Единичное имя обозначает один и только один предмет (луна, высочайшая вершина мира, человечество).
Общее имя обозначает более чем один предмет (книга, планета, химический элемент, человек).
Пустое, или беспредметное, имя не обозначает ни одного предмета (русалка; король, правящий во Франции в 1900 г.).
Имена делят также на конкретные (обозначает предмет, вещь или лицо) и абстрактные (обозначает свойство или отношения между предметами), что подчеркивал еще древнегреческий философ Антисфен: «Человека и лошадь я вижу, а человечности и лошадности не вижу».
Опираясь на интуитивную логику, определите, какие из умозаключений являются правильными:
- а) все математики — музыканты, значит, некоторые музыканты — математики;
- б) если к телу, движущемуся равномерно и прямолинейно, не подводится сила, оно движется без ускорения; тело движется без ускорения, значит, к нему не подводится сила;
- в) аргон, гелий, неон не горючи. Все они — инертные газы. Следовательно, инертные газы не горючи;
- г) все дифференцируемые функции непрерывны, следовательно, некоторые непрерывные функции дифференцируемые;
- д) некоторые люди умеют писать. Некоторые люди умеют читать. Значит, некоторые люди умеют и писать, и читать;
- е) глина — это жидкость или газ. Но глина — не газ, значит, глина — жидкость;
- ж) комедия, по определению Аристотеля, «есть подражание людям худшим, хотя и не во всей их подлости». Многие подражают худшим людям, хотя и нс идут в этом до конца. Значит, многие разыгрывают комедию;
- з) все растения дышат, микробы не дышат. Значит, микробы — не растения.
Среди общих имен выделяют понятия. Понятие — одна из форм мышления.
В XIX в. Г. Фрегэ выделил составляющие понятия. Понятие может быть раскрыто через такие составляющие, как термин, значение и смысл, связь между которыми, как мы писали в теме о понятиях (разд. II, параграф. 7.1), можно изобразить в виде семантического треугольника Фрегэ (рис. 21.3).
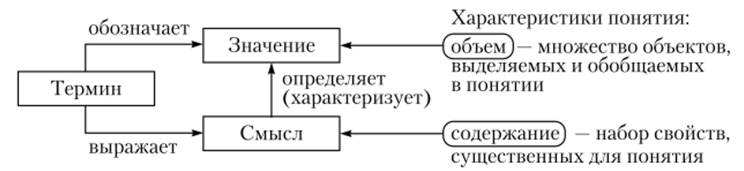
Рис. 213
Значение понятия отражено в его объеме — множестве объектов, которые описываются понятием. Учитывая, что знакомство с понятием лучше начинать с конкретных представителей, т. е. объема понятия, а именно множества объектов, входящих в понятие, то целесообразно познакомить учащихся с элементами теории множеств.
В современных образовательных стандартах для школы раздел «Элементы логики», как и раздел «История науки», выделен в самостоятельный методологический раздел, изучение которого может происходить на протяжении всего школьного курса математики.