Особенности ограничений для процедур оптимизации рентабельных цепей поставок

Для принятия решений по транспортному обеспечению поставок теперь требуется разобраться, как надо вести себя в общей ситуации, в частности если при оптимизации моделируемой системы управления запасами указанные выше условия (ограничения) (5.7) не будут выполняться. Напомним, что здесь такой вопрос надо обсуждать, причем применительно к анализу именно рентабельных цепей поставок. На формальном уровне в зависимости от показателей (параметров) рассматриваемой системы управления запасами ситуация, когда условия (ограничения) (5.7) не выполняются, для конкретной цепи поставок может быть обусловлена следующим:

• 1) не выполняется только первое из двух неравенств системы (5.7);
• 2) не выполняется только второе из двух неравенств системы (5.7);
• 3) не выполняются оба указанные выше неравенства системы (5.7).

Для рентабельных цепей поставок (именно такие, как уже было отмечено, только и рассматриваются здесь) последние два случая будут исключены автоматически. Действительно, в формате указанных случаев нельзя будет говорить о рентабельности цепи поставок, поскольку годовая прибыль не сможет покрыть расходы на поставку, на хранение товаров, а также на требуемые отчисления для поддержки бизнеса.

Как видим, в формате интересующих нас рентабельных многономенклатурных моделей управления запасами здесь осталось понять, как при оптимизации принимать решения применительно к следующей ситуации. Речь идет о ситуации, когда система неравенств (5.7) не выполняется, но только из-за нарушения именно первого из двух ее неравенств. При этом второе неравенство в системе (5.7) выполняется, соответственно работа цепи поставок является рентабельной. Факт (а точнее, возможность наступления такой ситуации) невыполнения первого из указанных неравенств (5.7) для соответствующей многономенклатурной EOQ-модели требует анализа следующих ситуаций:

• 1) накопленной к моменту времени Т_опт / 2 выручки не хватит, чтобы покрыть издержки хранения поставленного товара на соответствующем интервале повторного заказа [0; Г_опт], причем с учетом требуемых дополнительных отчислений на поддержку бизнеса;
• 2) накопленной к моменту времени Г_опт окончания интервала повторного заказа выручки уже будет достаточно, чтобы говорить об эффективной работе цепи поставок.

Как и в формате аналогичной EOQ-модели с одной номенклатурой поставляемого товара (см. гл. 1), нетрудно доказать, что такая ситуация для реальных рентабельных многономенклатурных цепей поставок на практике, как правило, будет невозможна. Поэтому при моделировании интересных для бизнеса цепей поставок такую ситуацию можно не рассматривать. Доказательство проведем методом от противного.

Итак, пусть для многономенклатурной EOQ-модели выполняется второе неравенство системы (5.7). Разумеется, этот факт подчеркивает рентабельность использования оборотного капитала в задаче транспортного обеспечения поставок и (или) эффективность работы такой цепи поставок. Соответственно, выполняется неравенство.

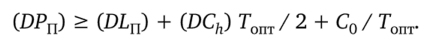
Кроме того, пусть при этом пусть не выполняется первое неравенство указанной системы, т. е. имеем:

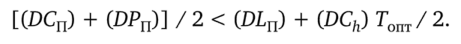
В последнем неравенстве выделим выражение [(DP_n) — (DL_n)], записав его в левой части такого неравенства. Кроме того, такое же выражение можно выделить и в предыдущем неравенстве (из последних двух, причем также в его левой части). После этого можно составить новое неравенство, сравнив верхнюю и нижнюю оценки для указанного выражения [(ДР_П) — (DL_n)].

При этом получим.

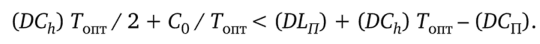
После упрощения окончательно имеем.

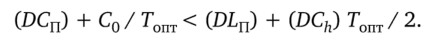
Теперь осталось обратить внимание на то, что при оптимальных параметрах стратегии управления запасами для многономенклатурной EOQ-модели годовые затраты на поставки совпадут с годовыми издержками хранения. Поэтому при оптимальной стратегии в последнем неравенстве всегда можно воспользоваться совпадением численных значений выражений С₀/ Г_опти (DC_h) Г_опт/ 2. После сокращения указанных совпадающих между собой выражений окончательно получаем следующее неравенство: (DC_n) < (DL_n).

На содержательном уровне в формате реальных цепей поставок такое неравенство, как уже отмечалось в гл. 1, скорее всего будет указывать на противоречие. Действительно, такое неравенство означает, что суммарные отчисления на поддержку бизнеса из выручки от реализованного товара должны быть больше, чем стоимость такого товара. Понятно, что для реальных цепей поставок такое условие вряд ли будет реально выполняться. Тем не менее с чисто теоретических позиций надо понимать, что указанный случай, когда выполняется неравенство.

(DC_n) < (DL_n), все-таки, возможен. Поэтому формально требуется продолжить анализ.

Такая ситуация будет иметь место (даже с учетом рентабельной работы цепи поставок), если для показателей анализируемой здесь многономенклатурной модифицированной EOQ-модели дополнительно будет выполняться следующее неравенство: (DC_n) < (DP_n), т. е. если товар будет приносить весьма большую прибыль.

Другими словами, при анализе конкретной цепи поставок товара при управлении запасами все-таки может оказаться, что не выполняется только первое из неравенств системы (5.7). При этом нами доказано, что это может случиться только в случае, когда суммарная годовая прибыль (DP_n) от поставляемого товара превысит суммарные годовые затраты на покупку такого товара (DC_n). Как отразится указанная ситуация на процедурах оптимизации работы рассматриваемой многономенклатурной цепи поставок? Соответствующие процедуры анализа идентичны тем, которые были представлены ранее в гл. 1 при анализе такой модели с одной номенклатурой товара.

Действительно, один из вариантов решения такой проблемы может состоять в том, что удастся изменить условия соответствующие контракту. Например, это будет иметь место в ситуации, когда в формате рассматриваемой здесь многономенклатурной EOQ-модели можно будет априори оговорить, что отчисления из выручки (выплаты вида L_ni) на поддержку бизнеса будут делаться не в середине, а в конце каждого интервала повторного заказа (т. е. в моменты времени, кратные Г_опт).

При такой модификации модели первое неравенство в системе неравенств (5.7) изменится. Оно при указанных новых условиях контракта будет соотноситься с ситуацией, когда выручка к моменту Т_опт /2 должна быть достаточной, чтобы покрыть только издержки хранения на интервале времени [0; Т_опт]. Указанные выплаты составят Т_опт №С_А) Т_опт/ 2]. Поэтому первое неравенство системы (5.7) примет новый вид: [(DC_n) + (DP_n)] > (DC_h) Г_опт.

Методом от противного теперь нетрудно доказать, что применительно к указанным новым условиям контракта по реализации отчислений на поддержку бизнеса всегда будет иметь место следующий важный факт, а именно покажем, что второе неравенство системы (5.7) для такой ситуации станет более общим (по отношению к первому неравенству). Это, в частности, будет означать, что первое неравенство такой системы в указанной ситуации станет просто следствием второго из двух отмеченных неравенств. Соответственно, такое первое неравенство (в указанном новом его виде) можно будет отбросить: в системе неравенств (5.7) в указанном случае вместо первых двух неравенств достаточно будет записывать только одно неравенство (второе). Другими словами, отмеченный здесь факт будет показывать, что анализ интересующей нас ситуации не требуется.

Приведем требуемое доказательство такого факта методом от противного.

Итак, пусть известно, что второе неравенство системы (5.7) выполняется. Как уже отмечалось, при оптимальных параметрах стратегии управления запасами имеет место равенство С₀ / Г_опт = (DC_h) Г_опт / 2. Воспользуемся этим, чтобы второе неравенство системы (6.7) записать в виде.

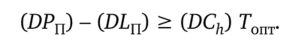
Кроме того, пусть при этом (от противного) не выполняется указанный новый вариант первого неравенства системы (5.7), т. е. имеет место неравенство.

Покажем, что приведенные последние два условия/неравенства всегда будут обусловливать противоречие с такими предположениями. Действительно, нетрудно видеть, что при выполнении двух последних разнонаправленных неравенств (которые относятся к выражению вида (DC/Д Т_опт) появляется возможность записать следующее неравенство:

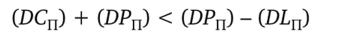
или, после сокращения,.

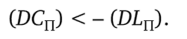
Оно, очевидно, противоречит здравому смыслу. Таким образом, требуемое утверждение доказано.

Как видим, нами доказан результат, который был отмечен выше. Пусть в формате рассматриваемой многономенклатурной EOQ-модели заранее принимается, что требуемые для поддержки бизнеса отчисления от выручки будут делаться в конце интервала повторного заказа. Тогда ситуация, относящаяся к случаю невыполнения системы неравенств (5.7), причем только из-за нарушения именно первого из двух ее начальных неравенств, всегда будет невозможна.

Более того, если второе неравенство системы (5.7) будет выполнено, то в указанных условиях (при указанном формате выплат отчислений на поддержку бизнеса) всегда будет выполнено и первое из условий (в указанном новом его формате) такой системы неравенств. Разумеется, в таких условиях при оптимизации решений о поставках первые два неравенства системы (5.7) надо заменить только одним неравенством (вторым). Кстати, в таком случае вместо указанного второго неравенства системы (5.7) также можно использовать эквивалентное неравенство (5.6).

Как видим, указанная проблема, относящаяся к формату нарушения системы неравенств (5.7) при оптимизации решений о поставках для многономенклатурных моделей управления запасами, действительно будет решена. Соответственно, для рентабельных цепей поставок отмеченную ситуацию (с нарушением только первого из неравенств указанной системы) при оптимизации запасов можно будет не рассматривать.

Как и в гл. 1, обратим также внимание на то, что указанную проблему можно решать и на основе другого подхода. Напомним, планируя работу цепи поставок, можно использовать заемный капитал для реализации требуемых отчислений на поддержку бизнеса, причем именно в середине интервала повторного заказа, если этого требует оптимизационная модель.

Конечно, в таких моделях потребуется также учесть, что из-за привлечения кредита изменится рентабельность оборотного капитала цепи поставок. В этом учебнике такие модели не рассматриваются. Изложение методов анализа моделей с использованием заемного капитала потребует формата отдельной работы.