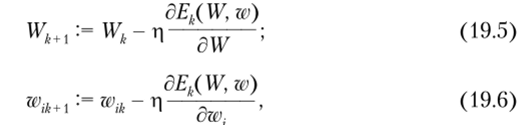Алгоритм обратного распространения ошибки

Самым распространенным способом обучения многослойных сетей является применение алгоритма обратного распространения ошибки, который относится к алгоритмам локальной оптимизации и соответствует принципиальной схеме итеративных методов, которая в общем виде представлена на рис. 19.3.

В схеме, показанной па рис. 19.3, описывается задача максимизации функции f (x) на области определения D, а также введены следующие обозначения: cor: D —*? D — корректирующее отображение, правило, согласно которому строится точка х_Ь1, если уже построены x_v х₂,…, х_к;

Р: R" —> R — оценочная функция, позволяющая для двух любых точек из R" определить, в какой мере одна «лучше» другой^[1].

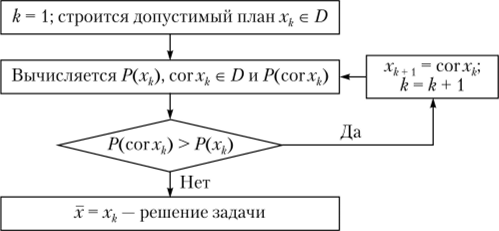
Рис. 193. Общая схема итеративных методов.

Применительно к задаче настройки весов многослойной нейронной сети изложенная выше схема решения экстремальных задач предстает в виде алгоритма, который может быть описан следующим образом.

Шаг 1. Весам сети присваиваются произвольные начальные значения.

Шаг 2. Выбирается очередная пара из обучающего множества (Х^к, Yj^[2]), k= 1…Nu вектор Х^к подается на вход.

Шаг 3. Вычисляется выход сети.

Шаг 4. Определяется разность между выходом, вычисленным сетью (значением, которое формируется последним слоем сети), и требуемым выходом Yj^[2]. Аналогом оценочной функции из описания общей схемы итеративных методов в данном случае является функция ошибки — Е_к, пропорциональная квадрату отклонения желаемого выхода от реального.

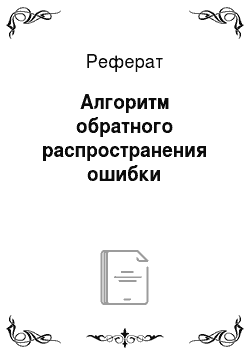
Шаг 5. Веса сети корректируются таким образом, чтобы минимизировать ошибку, для чего используется градиент функции ошибок. Корректирующее отображение для весов в случае двухслойной нейронной сети для классического варианта алгоритма обратного распространения ошибки определяется выражениями:

где W— вектор весов выходного слоя (предположим, что выходной слой состоит из одного нейрона); w_i — вектор весов, связанных с г-м нейроном скрытого слоя, i = 1,2, …, L; ц = const — коэффициент скорости обучения (О < ц < 1); k — номер итерации.

Шаг 6. Шаги со 2-го по 5-й повторяются до тех пор, пока ошибка для всех элементов обучающего множества не достигнет приемлемой малой величины или когда ошибка перестанет уменьшаться.

Шаги 4 и 5 как раз и составляют «обратный проход», за что алгоритм и получил свое название, так как здесь сигнал ошибки, первоначально определенной для последнего слоя, последовательно распространяется обратно по сети вплоть до входного слоя и используется для корректировки весов^[2].

• [1] Исследование операций: в 2 т. / пер. с англ. И. М. Макарова, И. М. Бескровного; подред. Дж. Моудера, С. Элмаграби. М.: Мир, 1981.
• [2] Круглов В. В., Дли М. И., Годунов Р. Ю. Указ. соч.
• [3] Круглов В. В., Дли М. И., Годунов Р. Ю. Указ. соч.
• [4] Круглов В. В., Дли М. И., Годунов Р. Ю. Указ. соч.