Теория графов. 
Конфликтология

Для изучения структурных характеристик конфликта в единой теории конфликтов используется теория графов. Она представляет важное математическое обобщение различной техники социально-психологического анализа — социограмм Я. Морено, ролевого анализа, треугольников Ф. Хайдера. Теория графов лежит в основе разнообразных методов анализа социальных сетей. В единой теории конфликта теория графов используется для построения структурных моделей конфликтов.

Структурная модель конфликта является базисной и состоит из следующих основных компонентов:

• 1) непустого множества элементов (субъектов) системы;
• 2) непустого множества отношений, в которых находятся элементы рассматриваемой социальной системы;
• 3) обозначения каждого отношения как позитивного или негативного (с возможной числовой характеристикой степени позитивности или негативности отношений).

Моделью, объединяющей все три указанных компонента, является означенный граф или диграф (ориентированный, направленный граф, все линии которого либо позитивные, либо негативные, либо смешанные).

Для исследования структурных характеристик конфликта как наиболее фундаментальных введем следующие определения из теории графов и диграфов.

Определение 1. Граф G = (X, Y) — структура, состоящая из конечного множества различных точек (вершин) X = {А, В, С,…} и множества неупорядоченных линий (ребер, дуг) Y= {АВ, ВА, АС,…}.

Точки графа обозначают объекты произвольной природы, его неупорядоченные линии — ненаправленные (симметричные) отношения между анализируемыми объектами. Граф можно рассматривать как модель системы с симметричными отношениями. Примеры графов приведены на рис. 2.2.

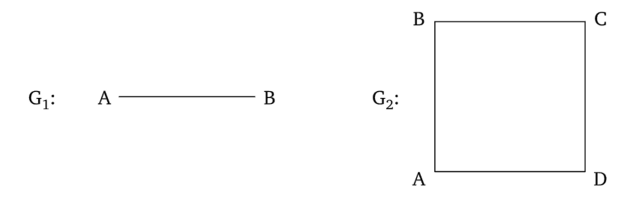
Рис. 2.2. Виды графов.

Допустим, графы G_: и G₂ обозначают одно и то же ненаправленное отношение — «быть знакомым». Тогда граф Считается: «А и В знакомы друг с другом», граф G₂: «А и В, В и С, С и D, D и, А попарно знакомы друг с другом (но, А и С, В и Бне являются попарно знакомыми)». Особенностью всех графов является то, что они обозначают симметричные (равные и обратно направленные) отношения. Отношение «быть знакомым», очевидно, симметричное, ибо еслиА знаком с В, то и В также должен быть знаком с А. Обратное также верно. Следовательно, в графах линии прямые и обратные вида АВ и ВА неразличимы: АВ = ВА.

Определение 2. Диграф (направленный, ориентированный граф) D= (X, Y) — граф, все или некоторые линии которого упорядочены.

Диграф — обобщение графа и используется для моделирования систем с симметричными и асимметричными отношениями. В диграфах прямые и обратные линии считаются различными, или упорядоченными (в паре АВ первым элементом является А, в паре ВА первым элементом является В). Таким образом, выполняется в общем случае неравенство: АВ Ф ВА. Диграф D, состоящий из двух точек, X = {А, В}, и двух упорядоченных линий, Y= {АВ, ВА}, изображен на рис. 2.3.

Рис. 2.3. Пример диграфа Риз двух точек и двух упорядоченных линий.

Если линию АВ интерпретировать как отношение «А отец В», тогда линия ВА будет обозначать отношение «В ребенок А». Если же линию АВ трактовать как «А левее В», тогда линия ВА будет обозначать «В правее А».

Пример диграфа D, состоящего из трех точек, X = {А, В, С}, и трех упорядоченных линий, Y= {АВ, СВ, СА}, изображен на рис. 2.4.

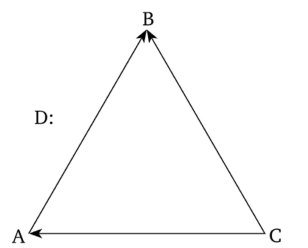
Рис. 2.4. Пример диграфа Риз трех точек и трех упорядоченных линий.

Если линия АВ обозначает отношение «А брат В», а линия СА — отношение «С племянник А», тогда линия СВ будет обозначать отношение «С сын В». Если же линию АВ интерпретировать как отношение «А больше В», линию СА как отношение «С больше А», тогда линия СВ будет обозначать отношение «С больше В».

Определение 3. Означенный граф (диграф) — граф (диграф), все или некоторые линии которого обозначены как положительные (позитивные), а остальные как отрицательные (негативные).

Пусть положительная линия символизируется как непрерывная и отрицательная — как прерывистая. Примеры означенного графа и диграфа приведены на рис. 2.5.

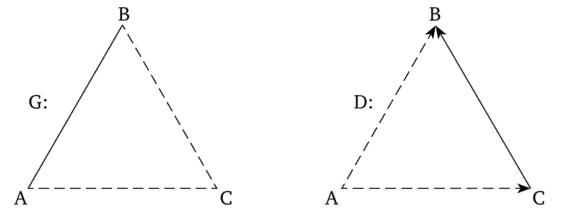
Рис. 2.5. Примеры означенного графа G и означенного диграфа D.

Пусть положительно обозначенная линия символизирует отношение «нравится» и отрицательно обозначенная линия — отношение «не нравится». Тогда линия АВ графа вчитается как «А и В оба нравятся друг другу», а, А и С, В и С — как «А и С, В и С оба не нравятся друг другу»; линия АВ диграфа D — как «В не нравится А», линия АС — как «С не нравится А», линия СВ — как «В нравится С» (обратные отношения не обозначены).

Определение 4. Путь графа (диграфа) — множество линий (упорядоченных линий) вида АВ, ВС, …, TS, в котором точки А, В, С, …, S различны.

Определение 5. Длина пути графа (диграфа) — число входящих в него линий.

Определение 6. Цикл графа (диграфа) — путь графа (диграфа) вместе с линией, соединяющей первую и последнюю точки.

Определение 7. Цикл графа называется простым, если ни одна из образующих его точек не встречается более одного раза.

Понятия цикла достаточно для анализа графов, но недостаточно для анализа диграфов. Обобщением цикла выступает понятие полуцикла согласно следующему определению.

Определение 8. Полуцикл диграфа — цикл графа (диграфа), образованный взятием только одной линии из каждой пары АВ или ВА, ВС или СВ, … множества всех его возможных линий.

Каждый цикл является полуциклом, но обратное в общем неверно. Каждый цикл длиной 2 представляет цикл. Принципиальное отличие цикла от полуцикла, интерпретируемое графически, состоит в том, что, двигаясь по его линиям от любой точки (вершины), мы всегда через некоторое число линий к ней же и вернемся; в случае полуцикла такой возврат в общем случае не гарантируется. Как будет показано в следующем параграфе, данное свойство циклов, обозначающее петлю обратной связи, определяет все динамические свойства конфликтов.

Пример неозначенного диграфа D, содержащего три полуцикла, из которых только один является циклом, приведен на рис. 2.6.

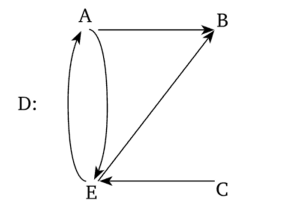
Рис. 2.6. Пример диграфа D с одним циклом и тремя полуциклами.

Согласно рис. 2.6, диграф D имеет следующие полуциклы:

• 1. АЕ, ЕВ, АВ (не является циклом)
• 2. ЕА, ЕВ, АВ (не является циклом)
• 3. АЕ, ЕА (является циклом)

Определение 9. Цикл и полуцикл диграфа считаются простыми, если ни одна из его точек не встречается более одного раза.

Далее рассматриваются только простые циклы и полуциклы.

Определение 10. Знак Бцикла графа (полуцикла диграфа) равен произведению знаков его линий и вычисляется согласно следующим правилам (знак «+» символизирует положительную модальность отношения, знак «-» — отрицательную модальность отношения):

Согласно приведенным правилам, цикл (полуцикл) имеет знак «+», если содержит нулевое или четное число отрицательных линий, и имеет знак «-», если содержит нечетное число отрицательных линий.

Допустим, дан означенный диграф D, содержащий следующие полуциклы (рис. 2.7):

• 1. АС, С, А (цикл).
• 2. АВ, СВ, АС (не цикл).
• 3. АВ, СВ, СА (не цикл).

Рис. 2.7. Пример означенного диграфа D с одним циклом и тремя

полуциклами Согласно определению 10, полуциклы диграфа DHa рис. 2.7 имеют следующие знаки:

• 1. s (AC, СА) = s (AC) х s (CA) = (-) х (-) = (+).
• 2. s (AB, СВ, АС) = s (AB) х s (CB) X s (AC) = (+) х (+) X (-) = (-).
• 3. s (AB, СВ, СА) = s (AB) х s (CB) х s (CA) = (+) х (+) х (-) = (-).

Определение 11. Полуцикл (цикл) сбалансирован, если его знак равен «+ «(содержит нулевое или четное число отрицательных линий), и несбалансирован, если его знак равен «-» (содержит нечетное число отрицательных линий).

Второй и третий полуциклы диграфа D на рис. 2.6 не сбалансированы, так как их знаки отрицательные. Сбалансированность полуцикла означает, что знаки его элементов совместимы друг с другом, что все его элементы, если полуцикл является циклом, охвачены положительной обратной связью. Несбалансированность полуцикла (цикла) свидетельствует о несовместимости знаков его элементов, потому что если полуцикл является циклом, то его элементы охвачены отрицательной обратной связью.

Как отмечалось, между циклами и полуциклами имеется существенное структурное различие — в циклах начальная и конечная точки всегда совпадают, а в полуциклах не всегда. Но в означенных диграфах это различие теряет свое значение. Принципиальной характеристикой означенного диграфа остается лишь знак его цикла или полуцикла. Независимо от того, является ли данный полуцикл циклом или нет, только его знак свидетельствует о совместимости или несовместимости его элементов. Иными словами, в означенных диграфах решающее значение приобретает знаковая совместимость и несовместимость элементов.

Определение 12. Означенный граф (диграф) сбалансирован, если и только если все его циклы (полуциклы) имеют позитивный знак.

Второй и третий полуциклы диграфа D на рис. 2.6 не сбалансированы. Значит, и диграф D не сбалансирован.

Определение 13. Означенный граф (диграф) является конфликтным, если и только если он не сбалансирован.

Конфликтный граф символизирует структуру знакового противоречия, конфликтный диграф — структуру комплементарно-знакового противоречия. Примеры конфликтного графа и диграфа, моделирующих знаковое и комплементарно-знаковое противоречие, приведены на рис. 2.8.

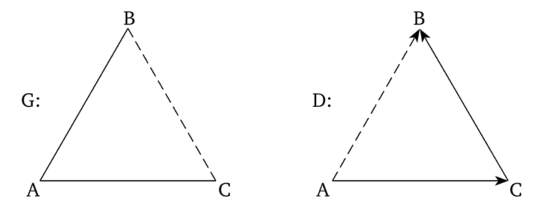
Рис. 2.8. Примеры конфликтного графа G и диграфа D.

Формальным критерием наличия конфликта может служить, во-первых, то, что каждый элемент несбалансированной системы находится в несовместимых отношениях с каждым другим ее элементом, и, во-вторых, то, что каждый элемент находится в негативном отношении к самому себе. Оба условия эквивалентны друг другу. Например, согласно графу G на рис. 2.7, элемент, А позитивно связан с элементом В посредством линии АВ и одновременно негативно связан с В посредством линий АС, СВ. Аналогично для элементов В и С. Если выбрать элемент, А (элементы В или С соответственно) в качестве начала и конца цикла в этом же графе, знак цикла будет отрицательным. Значит, каждый элемент конфликтного цикла (полуцикла) находится в отношении отрицательной обратной связи с самим собой.

Определение 14. Сбалансированный граф (диграф) называется синергетическим (символизирует синергетический способ разрешения конфликта), если и только если каждый его полуцикл содержит нулевое число отрицательных отношений.

Примеры синергетического графа и диграфа с одним полуциклом приведены на рис. 2.9 (все отношения положительно означены).

Рис. 2.9. Примеры синергетического графа G и диграфа D.

Смысл синергизма состоит в объединении всех элементов системы в одну общую «дружественную» коалицию, члены которой относятся друг к другу и к самим себе только положительно. Формальное условие такого объединения — отсутствие негативных линий (отрицательных отношений) между элементами системы.

Определение 15. Сбалансированный граф (диграф) называется антагонистическим (символизирует антагонистический способ разрешения конфликта), если и только если он содержит четное число отрицательных линий.

Примеры антагонистического графа и диграфа с одним полуциклом приведены на рис. 2.10.

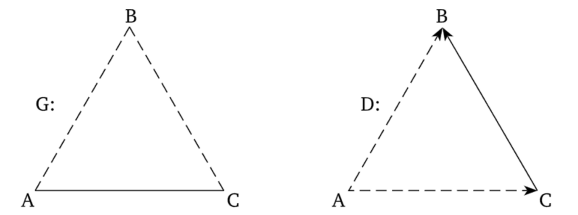
Рис. 2.10. Примеры антагонистического графа G и диграфа D.

Смысл антагонизма состоит в разделении всех элементов системы на две (и только две) «враждующие» коалиции, члены каждой из которых относятся друг к другу и к самим себе положительно, а к каждому члену «враждебной» коалиции отрицательно.

Теория графов позволяет сформулировать множество теорем о структурных свойствах конфликтных и бесконфликтных систем^[1]. Здесь без доказательства будет приведена только одна теорема.

Фундаментальная структурная теорема анализа и разрешения конфликтов. Система из n > 1 элементов, все отношения которой означены, находится в бесконфликтном состоянии, если и только если это состояние либо синергетическое, либо антагонистическое.

Фундаментальная структурная теорема (ФСТ) занимает в теории анализа и разрешения конфликтов особое место, и имеет смысл остановиться на разъяснении ее конфликтологического значения более подробно.

Трудоемкую процедуру выявления всех циклов, определения их знаков и сбалансированности ФСТ заменяет более эффективной техникой определения конфликтности/бесконфликтности исследуемой системы. Рассмотрим пример. Известно, что принцип сбалансированности отношений симпатии и антипатии (дружбы и вражды) давно нашел отражение в следующих правилах бесконфликтного общения:

• 1. Друг моего друга — мой друг.
• 2. Друг моего врага — мой враг.
• 3. Враг моего друга — мой враг.
• 4. Враг моего врага — мой друг.

Согласно ФСТ теореме, каждому из приведенных правил соответствует определенное бесконфликтное состояние системы из трех элементов, вместе характеризующих ее потенциал бесконфликтности (табл. 2.2).

Таблица 2.2

1.	AB — «А — друг В» ВС = «В — друг С» АС = «А — друг С».		Синергетическое состояние: все отношения между А, В и С положительные (А, В и С образуют одну коалицию).
2.	АВ — «А — враг В» ВС = «В — друг С» АС — «А — враг С».		Антагонистическое состояние № 1: А, с одной стороны, В и С — с другой, образуют две антагонистические коалиции.
3.	АВ — «А — друг В» ВС = «В — враг С» АС = «А — враг С».		Антагонистическое состояние № 2: А и В, с одной стороны, С — с другой, образуют две антагонистические коалиции.
4.	АВ = «А — враг В» ВС = «В — враг С» АС = «А — друг С».		Антагонистическое состояние № 3: В, с одной стороны, А и С — с другой, образуют две антагонистические коалиции.

Все четыре означенных диграфа из табл. 2 символизируют бесконфликтные состояния рассматриваемой системы, состоят из одного множества элементов, п = 3, и содержат один и тот же полуцикл: АВ, ВС, АС. Согласно теореме 2, в системе с тремя элементами допустимо 23 — 1 = 4 бесконфликтных состояния. Из них одно синергетическое (первое в табл. 1) и три антагонистических (со второго по четвертое).

Первое бесконфликтное состояние системы характеризуется тем, что все п = {А, В, С} элементов соединены позитивными линиями. Нет ни одной негативной линии. Следовательно, все элементы образуют синергетическую коалицию, и притом единственную, т = 1. Согласно второму бесконфликтному состоянию, элемент, А негативно связан как с элементом В, так и с элементом С, но последние два элемента соединены друг с другом позитивной линией. Следовательно, имеет место непротиворечивое разбиение множества элементов на антагонистические коалиции: rrij = {А} и т₂ = (В, С}. Согласно третьему бесконфликтному состоянию, элемент, А позитивно связан с элементом В, но как элемент А, так и элемент В негативно связаны с элементом С. Следовательно, и здесь все элементы непротиворечивым образом разбиваются на антагонистические коалиции т₁ = {А, В} и т₂ = {С}. Наконец, согласно четвертому бесконфликтному состоянию, элемент, А позитивно связан с элементом С, а элемент В негативно связан как с элементом А, так и с элементом С. Следовательно, и здесь имеет место непротиворечивое разбиение всех элементов на антагонистические коалиции ml — {А, С} и т₂ — {В}.

Рассмотренные разбиения исчерпывают все допустимые варианты бесконфликтного состояния рассматриваемой системы (бесконфликтный потенциал данной системы). В системе из трех элементов допустимо 23 = 8 различных распределений положительных и отрицательных отношений. Так как четыре из них бесконфликтные, оставшиеся четыре, согласно теореме 3, являются конфликтными и вместе характеризуют конфликтный потенциал данной системы (табл. 2.3).

Таблица 2.3

1.	AB = «А — друг В» ВС = «В — друг С» АС — «А — враг С».		Конфликтное состояние № 1: никакие коалиции между А, В и С невозможны).
2.	АВ — «А — враг В» ВС — «В — друг С» АС = «А — друг С».		Конфликтное состояние № 2: никакие коалиции между А, В и С невозможны.
3.	АВ = «А — друг В» ВС = «В — враг С» АС = «А — друг С».		Конфликтное состояние № 3: никакие коалиции между А, В и С невозможны.
4.	АВ = «А — враг В» ВС — «В — враг С» АС = «А — враг С».		Конфликтное состояние № 4: никакие коалиции между А, В и С невозможны.

В рассмотренном примере означенные диграфы состояли из одного полуцикла. Модели реальных конфликтов могут содержать хотя и конечное, но очень большое число полуциклов. В этом случае ФСТ позволяет сформулировать алгоритм, быстро и безошибочно дифференцирующий системы на конфликтные и бесконфликтные с любым числом элементов и циклов (полуциклов).

Алгоритм распознавания конфликтных и бесконфликтных состояний

1. Составляется список всех элементов панализируемой системы в произвольном порядке. Пусть т_х и т₂ обозначают взаимно исключающие и совместно исчерпывающие множество всех элементов пподмножества.

• (коалиции) (n= m₁um₂; m₁nm₂ = 0). До начала разбиения пмножества mj и ш₂являются пустыми. Произвольно выбирается элемент, скажем А, и включается в множество пц в качестве первого элемента.
• 2. Произвольно выбирается из списка пновый элемент, скажем В, и сравнивается с А. Если элементы, А и В связаны только позитивно (простыми и сложными путями), то элемент В включается к множество /Пц если они связаны только негативно (простыми и сложными путями), то элемент В включается в множество ш₂.
• 3. Выбор элементов проводится последовательно до полного исчерпания списка или до обнаружения элемента, который одновременно принадлежит обоим множествам т₁ и т₂.
• 4. Если все элементы писчерпывающим образом разделились на множества ш_г и ш₂, причем множество ш₁или множество т₂, но не оба, может оказаться пустым, тогда анализируемая система бесконфликтна; в противном случае, т. е. когда существует хотя бы один элемент, который принадлежит обоим множествам гщ, и ш₂ одновременно, она конфликтна.

Проанализируем басню Эзопа «Убийца», в которой имеется несколько участников и циклов (потенциально восемнадцать), с помощью указанного алгоритма.

Некий человек совершил убийство, и родственники убитого его преследовали. Он прибежал к реке Нил, но тут столкнулся с волком. В страхе он забрался на дерево, нависшее над рекой, но увидел змею, которая там раскачивалась. Тогда он бросился в воду; тут-то крокодил его подстерег и сожрал.

Басня показывает, что для человека, запятнанного преступлением, ни земля, ни воздух, ни вода не будут убежищем. В данной басне формально есть пять участников конфликта; убийца, родственники погибшего, волк, змея и крокодил. Фактически волк, змея и крокодил персонифицируют функцию неотвратимого возмездия. Предмет конфликта — желание убийцы избежать расплаты. Причина конфликта — несовместимость тяжести совершенного преступления с желанием избежать справедливого наказания. Введем обозначения: У = «Убийца», Ж = «Желание убийцы избежать расплаты», В = «Волк», 3 = «Змея», К = «Крокодил».

Модель конфликта (означенный граф) в развернутом виде изображена на рис. 2.11.

Рис. 2.77. Модель конфликта басни «Убийца».

Означенный граф на рис. 2.11 содержит шесть циклов, из которых только три сбалансированы.

• — Цикл (ВЗ, ЗК, КВ) сбалансирован, так как содержит нулевое число негативных отношений.
• — Цикл (ВЗ, ЗК, КЖ, ЖВ) сбалансирован, так как содержит четное число негативных отношений.
• — Цикл (ВК, КЖ, ЖВ) сбалансирован, так как содержит четное число негативных отношений.
• — Цикл (ВЖ, ЖУ, УВ) не сбалансирован, так как содержит нечетное число негативных отношений.
• — Цикл (ВК, КЖ, ЖУ, УВ) не сбалансирован, так как содержит нечетное число негативных отношений.
• — Цикл (ВЗ, ЗК, КЖ, ЖУ, УВ) не сбалансирован, так как содержит нечетное число негативных отношений.

Система, состоящая из произвольного числа элементов, конфликтна, если содержит по крайней мере один несбалансированный цикл. Система на рис. 2.10 содержит три несбалансированных цикла. Значит, она конфликтна. Желанию убийцы спастись препятствуют все три стихии, без которых человек не может существовать: земля, воздух и вода.

Проверим эффективность алгоритма. Список участников рассматриваемой басни Эзопа равен множеству п = {В, 3, К, Ж, У}.

Выберем В в качестве первого элемента и поместим его в т_у Получаем Х_х = {В} и т₂ = 0.

Выберем 3 в качестве второго элемента. Этот элемент связан с В позитивной линией (общий знак всех простых и сложных путей от В к 3 положительный). Значит, т₁ = {В, 3} и т₂ = 0.

Выберем К в качестве третьего элемента. Этот элемент связан с В и 3 позитивно (общий знак всех простых и сложных путей от К к В и 3 положительный). Значит, т₁ = {В, 3, К} и т₂ = 0.

Выберем Ж в качестве четвертого элемента. Этот элемент связан с В, 3 и К негативно (общий знак всех простых и сложных путей от Ж к К, В и 3 отрицательный). Значит, т₁ = {В, 3, К} и т₂ = {Ж}.

Пятый и последний элемент из списка — У. Общий знак таких линий, как УВ, УВЗ, УВК, УВКЗ, является положительным, что свидетельствует о совместимости У с элементами В, 3 и К. Но общий знак линии УЖ также является положительным, что говорит о совместимости У с элементом Ж. Значит, истинно т₁ = {В, 3, К, У} и т₂ = {Ж, У}. И так как элемент У принадлежит двум несовместимым множествам т_х и т₂ одновременно, то рассматриваемая система конфликтна. Также ясно, что причиной конфликта является амбивалентность (противоречивость) отношений элемента У. Он хочет спастись, но не может противостоять ни одной из мстящих ему вместе с родственниками стихий.

Результаты проведенного анализа суммирует означенный граф на рис. 2.12. Он показывает причину конфликта — несбалансированность элементов множеств Х_г и т₂: элемент У принадлежит двум несовместимым множествам — т₁ = {В, 3, К} и т₂ = {Ж}.

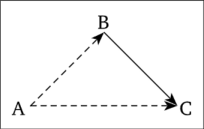
Рис. 2.12. Результат структурного анализа модели конфликта басни «Убийца».

Эзоп, как и подобает баснописцу, предлагает свое решение конфликта. Оно сводится к последовательному лишению убийцы всякой надежды на спасение на земле, в воздухе и воде и, как результат, к его смерти в водах Нила (рис. 2.13).

Проверим, действительно ли означенный граф на рис. 2.12 является бесконфликтным.

Как и прежде, п = {В, 3, К, Ж, У}. ВыберемВ в качестве первого элемента. Тогда т₁ = {В} и т₂ = 0.

Выберем 3 в качестве второго элемента. Этот элемент связан с В позитивно (общий знак всех простых и составных линий от В к 3 положительный). Значит, т₁ = {В, 3} и т₂ = 0.

Выберем К в качестве третьего элемента. Этот элемент связан с В и 3 позитивно (общий знак всех простых и составных линий от К к В и 3 положительный). Значит, т₂ = {В, 3, К} и т₂ = 0.

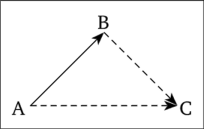
Рис. 2.13. Решение конфликта басни «Убийца».

Выберем Ж в качестве четвертого элемента. Этот элемент связан с В, 3 и К негативно (общий знак всех простых и составных линий от Ж к К, В и 3 отрицательный). Значит, = {В, 3, К} и т₂ = {Ж}.

Пятым и последним элементом является У. Общий знак таких линий, как УВ, УВЗ, УВК, УВКЗ, является положительным, что свидетельствует о совместимости У с элементами В, 3 и К. Общий знак линии УЖ является отрицательным, что говорит о несовместимости У с элементом Ж. Значит, истинно т₂ = {В, 3, К, У} и т₂ = {Ж}. При этом п = = т₂и т₂и т₂пт₂ = 0.

Так как все элементы множества нразделены на два взаимно исключающих и совместно исчерпывающих множества т₂ и т₂, то рассматриваемая система бесконфликтна. Исчезла амбивалентность в отношениях элемента У с другими элементами. Теперь элемент У принадлежит только множеству m_x.

• [1] См.: Светлов В. А.

  Введение

  в единую теорию анализа и разрешения конфликтов.М., 2009. С. 62−66.