Математика в свете философских категорий

Математика — естественный язык выражения взаимосвязи метафизики и идеи Единого или Логоса.

Жак Даррида

Начнем с перечисления основных сопоставлений «философия — математика»:

• • идеальное — математическая теория (понятие, идея);
• • материя — математический объект, математическая модель, структура, конструкция;
• • движение — функция, отображение;
• • количество — число, величина, мера;
• • качество — отношение эквивалентности;
• • форма — геометрическая фигура, формула;
• • содержание — класс моделей теории, объем понятия;
• • явление — математический факт или рассуждение;
• • сущность — модельные примеры, характеризация;
• • мера — инвариант, координаты, мера;
• • всеобщее — законы логики, универсальное множество;
• • особенное — множество, класс;
• • единичное — элемент множества;
• • целое и часть — множество и его подмножество;
• • внутреннее — элементы и части математической структуры;
• • внешнее — то, что находится вне математического объекта;
• • причина — достаточное условие теоремы;
• • следствие — необходимое условие теоремы;
• • причинно-следственная связь — логическое следование;
• • метод — способ доказательства или построения, алгоритм;
• • бытие — существование;
• • действительное — имеющее модель;
• • разумное — непротиворечивое;
• • возможное, случайное — вероятность;

• • закон, истина — теорема, доказательство;
• • свобода — свободный (универсальный) объект;
• • необходимость — необходимое условие;
• • пространство — различные виды пространств;
• • время — числовая прямая;
• • порядок — порядковая структура;
• • система — математическая структура;
• • отношение — n-арное отношение (где п — кардинал);
• • действие — алгебраическая операция, преобразование;
• • состояние — точка фазового пространства;
• • симметрия — группа;
• • сохранение — гомоморфизм;
• • тождество — изоморфизм;
• • конечное и бесконечное — мощность множества;
• • дискретное и непрерывное — свойства порядковой структуры.

Рассмотрим подробнее эти категории и их взаимосвязи. Идеальное в математике — это ее идеи, понятия, методы, теории. Материальное выражается в конкретных математических структурах и конструкциях. Категории идеального и материального в математике обе принадлежат сфере математического сознания, но представляют абстракции разного уровня (скажем, понятия и примеры). В приложениях математики акценты смещаются: весь математический аппарат предстает как идеальное, а описываемые объекты или специальные модели суть материальное.

Реальное движение, любое изменение можно попытаться описать функционально, то есть с помощью той или иной функции. Законы движения часто выражаются решениями дифференциальных уравнений. В математике изучаются различные виды функций (числовые функции, алгебраические операции, геометрические преобразования, непрерывные отображения и т. д.); на данной основе возможно разбиение (классификация) математики на отдельные математические дисциплины. Находят применение и так называемые многозначные функции (соответствия). Отметим, что категория «движение» проявляет себя в самых разнообразных ситуациях и раскрывается, конкретизируется через целый ряд понятий: изменение, развитие, становление, преобразование, процесс, действие (производные от него — воздействие, взаимодействие, противодействие) и т. п.

Количество — это, прежде всего, числа: кроме действительных чисел в математике существуют комплексные числа, кватернионы, октавы (числа Кэли), двойные и дуальные числа, р-адические числа, различные «числоподобные» объекты, изучаемые в современной алгебре. К категории количества относится и понятие величины, предполагающее упорядоченность, сравнение элементов по величине. Понятие величины еще ожидает серьезного методологического анализа.

Классификация (разбиение) объектов по определенному качественному признаку (животных — по родам или видам, физических тел — по размерам или форме, чисел — по арифметическим характеристикам) определяется соответствующим отношением эквивалентности. Переход от множества объектов к классам эквивалентных объектов называется факторизацией этого множества. На этом пути в математике появились фундаментальные понятия конгруэнции и факторструктуры.

Форма как категория воплощается в понятии геометрической фигуры и ее обобщениях (различные типы пространств), изучаемых в геометрии и топологии. Под эту категорию подпадает и значение схема. Математические формулы являются формой соответствующих понятий и предложений математики. Под содержанием абстракции мы понимаем класс всех ее моделей (примеров). Содержанием математической теории можно считать, наряду с моделями, множество ее теорем (доказуемых утверждений). Процесс формализации изучаемого объекта — это поиск удобной формы его представления. Формализация содержательной математической теории приводит к формальной аксиоматической системе, выраженной на символьном языке математической логики. Выкладки и вычисления в формальной системе можно автоматизировать, то есть поручить компьютеру (этим занимается компьютерная алгебра).

Подчеркнем, что математика изучает и описывает мир посредством «внешних» категорий количества и формы. Тем самым универсальность и эффективность математики, являющиеся проявлениями единства мира, обосновывают первостепенную роль категорий количества и формы в системе всех философских категорий.

Математическое явление трактуется и как математическая закономерность, и как процесс рассуждения. Все, так или иначе, является, проявляется. Явление — это некое проявление сущности. Поэтому термин «явление» можно трактовать очень широко — как вещь, процесс, отношение, что позволяет отнести эту категорию к числу первичных, основополагающих философских категорий. Сущность математической абстракции (понятия, теории) заключается в ее модельных примерах — образцовых моделях, «супермоделях» данной абстракции. Модельным примером абстракции считается такая модель этой абстракции, в которой так или иначе (с помощью математических и логических конструкций) отражаются все ее существенные (структурные) свойства [88]. Модельные примеры служат «материальным» воплощением самой сути абстракции.

Мера на языке философии означает количественно заданный интервал сохранения качественной идентификации объекта. В математике существует свое понятие меры, определяемое как аддитивная неотрицательная вещественнозначная функция, заданная на алгебре множеств. С ним тесно связаны однокоренные понятия измеримости (множеств и функций) и размерности (пространств). Более общим является понятие величины, которая может принимать нечисловые значения. Сравнимость по величине ассоциируется также с понятиями порядка и упорядоченного множества. Мы видим, что категория меры проявляется в математике в качестве количественного оценивания и структуризации объектов.

Категория всеобщее проявляется, прежде всего, в законах логики. Всеобщее связано как с квантором общности, так и с понятием универсального (всеобъемлющего) множества. В рамках фиксированной математической теории в качестве всеобщего выступают общезначимые предложения (формулы), которые по определению истинны в любой модели данной теории. Особенное (обособленное), помимо множества, можно толковать как отдельную тему или область математики, чему соответствует деление математики на дисциплины: теория чисел, алгебра, геометрия, математический анализ, теория вероятностей, математическая логика и т. д. Единичное — это и элемент (точка) множества, и уникальный математический объект: натуральный ряд, числовая прямая, действительная плоскость, число п. Элементы и подмножества относятся к содержащему их множеству как часть к целому. Натуральные (целые) числа составлены из единиц, а дроби суть суммы равных частей целого числа, частные целых чисел.

Рассматривая категории внутреннего и внешнего в математике, мы, прежде всего, имеем в виду внутреннее (локальное) или внешнее (глобальное) изучение математических объектов. При первом подходе строение математического объекта анализируется и выражается через его элементы и подобъекты. При внешнем подходе изучаемый математический объект берется как элемент категории себе подобных объектов с соответствующими морфизмами, связывающими объекты. При этом используются только сами морфизмы и свойства композиции морфизмов данной категории. Важную роль в математике играют, например, следующие категории: группы и их гомоморфизмы, топологические пространства и непрерывные отображения между ними, упорядоченные множества и изотонные отображения.

Отметим, что в математике, как показал французский математик Ловер, теоретико-множественный (внутренний) и теоретико-категорный (внешний) подходы равносильны, они имеют одинаковую выразительную силу. Пусть, например, рассматривается множество А = (а, б, в, г, д, е} в категории всех множеств и их отображений. Нужно найти число элементов этого множества, не пересчитывая их непосредственно. Фиксируем некоторый финальный объект F категории множеств. Напомним: объект F категории называется финальным, если из любого объекта данной категории существует один-единственный морфизм в F. Легко видеть, что в категории множеств финальные объекты — это в точности одноэлементные множества. Подсчитав число морфизмов из F в Л, получим 6 морфизмов — по одному для каждого элемента (буквы) множества Л.

Причинно-следственная связь представляет собой логический вывод, справедливость которого устанавливается доказательством заключения теоремы на основе ее посылок (условия). Теорему всегда можно сформулировать в виде импликации Л => В; при этом утверждение А называют достаточным условием для (выполнения) утверждения В, а А — необходимым условием для В. Одна и та же теорема может быть доказана различными методами. Термин «метод» применим и к построениям, алгоритмам, вычислениям и преобразованиям.

Понятия возможного и невозможного (события) находят свое выражение в теории вероятностей.

Далее, вспомним знаменитое положение Гегеля «Все действительное разумно, все разумное действительно», которое естественно интерпретировать как теорему Геделя: непротиворечивость формальной математической теории равносильна существованию ее модели. Здесь разумное трактуется как непротиворечивое, а действительное — как существование модели. С этой теоремой связана другая теорема Геделя — о полноте: формула формальной теории является теоремой тогда и только тогда, когда она общезначима. Приведем еще созвучное высказывание Лейбница: «Что мыслимо — то возможно, что возможно, то мыслимо».

Философскому и общенаучному понятию истины в математике отвечает понятие теоремы, определяемой как доказуемое утверждение. В содержательной математике (в которой не формализована логика) или в конкретной математической модели истина имеет семантическое (смысловое) понимание. Однако в достаточно богатой формальной аксиоматической теории понятие истины невыразимо на языке этой теории, что утверждает теорема Тарского. По теореме Геделя о неполноте, в таких формальных теориях существуют заведомо истинные — в стандартной модели натурального ряда — формулы, не являющиеся теоремами (существование недоказуемых истин).

Подобные предложения (формулы) строятся с помощью так называемого диагонального канторовского метода как некоторые утверждения о геделевых номерах самих предложений. Говоря очень упрощенно, получаются предложения типа «То, что здесь написано, нельзя доказать» или «Я — не теорема». В непротиворечивой системе (формальной теории) данное предложение не может быть ложным, так как доказуемые предложения (теоремы) истинны. Следовательно, получаем истинное, но недоказуемое предложение. Точно так же невозможно доказать непротиворечивость самой формализованной математики. Нельзя адекватно формализовать всю математику, большинство ее содержательных разделов. Философски эти логико-математические утверждения означают, что не существует формальной научной системы, в рамках которой можно точно выразить, описать все многообразие мира. Расширяя и совершенствуя научную систему мироздания, мы на любом этапе познания будем иметь что-то непознанное, а возможно, и принципиально непознаваемое. Наверное, одного научного (математического) способа познания мира недостаточно. Интуитивное и иррациональное проявляются и в философии, и в художественном восприятии мира, и в религиозном откровении.

Некоторые философские положения (см. цитированные выше высказывания Гегеля и Лейбница) легко обретают математический вид. Так, первую триаду Гегеля из его «Науки логики».

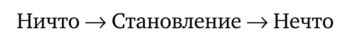
можно представить как процесс (Становление) получения {} из пустого (Ничто) множества 0 одноэлементного (Нечто) множества {0}. Применяя подобную процедуру неограниченное число раз, получим модель натурального ряда с нулем:

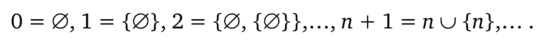
Вспомним также пифагорейское учение «Все есть натуральное число» и тезис Кронекера «Бог создал натуральные числа, а все остальное в математике — дело человеческого разума». Эти общие положения говорят о том, что всю математику можно построить на основе одних только натуральных чисел, причем строго логически при помощи тех или иных конструкций, что во многом было осуществлено в XX веке. Сам натуральный ряд был аксиоматизирован итальянским математиком Пеано в конце XIX века.

В марксистском определении категории свобода — «Свобода есть осознанная необходимость» — имеется довольно глубокий смысл, обнаруживающий себя и в математике. В различных разделах математики (универсальная алгебра, общая топология) существуют так называемые свободные объекты — они свободны от всех соотношений и дополнительных условий, не являющихся необходимыми, то есть не вытекающих из аксиом данной теории. Значение свободных объектов в категории родственных объектов заключается в том, что все объекты данного класса получаются из свободных объектов как их факторобъекты.

Априорно пространство представляется нам как вместилище всевозможных вещей, общее место реальных событий, протяженная пустота. Изучаемые в математике пространства по своему происхождению имеют геометрическую природу — это евклидовы, векторные, аффинные, проективные, метрические, топологические пространства, пространства с мерой. Развиваясь в основном в лоне геометрии и топологии, понятие пространства приобрело весьма абстрактный и многозначный смысл. Назовем также пространства Лобачевского, Римана, Минковского, конечные аффинные и проективные плоскости и пространства, фазовое пространство, пространство событий. Понятия пространства, точки, фигуры наглядны, служат образной основой геометрической терминологии, широко применяемой, помимо геометрии, в линейной алгебре, математическом анализе, топологии, теории графов.

Время, мыслимое как (направленная) числовая прямая, не имеет ни начала, ни конца. Любой отрезок времени ограничен, имеет начало и конец, но как множество он континуален, содержит бесконечно много мгновений. Заметим, что существует естественнонаучная гипотеза о дискретности времени (пространства, движения): время квантовано, то есть состоит из отдельных неделимых частичек (квантов), при этом любой промежуток времени является конечной последовательностью таких «протяженных мгновений». Четырехмерное «пространствовремя» играет важнейшую роль в специальной теории относительности.

Категория порядка, или упорядоченности, отражается как в самом понятии математической структуры, уточняющем категорию системы, так и в его важнейшем частном случае — порядковой структуре. Порядковая структура реализуется в таких понятиях, как отношение порядка, упорядоченное множество, упорядоченная алгебраическая или топологическая система. Отсутствие порядка есть хаос. Мерой хаоса, неорганизованности или неопределенности выступает энтропия.

Каждая система определяется множеством своих отношений, характеризующих взаимосвязи составляющих ее элементов. Если п — натуральное число, даже произвольное трансфинитное число (ординал), то п-арное отношение на множестве связывает некоторые n-ки элементов этого множества. Частными случаями понятия н-арного отношения являются бинарные отношения (функции, эквивалентности, отношение порядка), алгебраические операции, предел последовательности. Понятия алгебраической операции, вычисления, преобразования, алгоритма относятся к категории действие. Производной является категория деятельности, играющая важную роль в философии, психологии, педагогике и методике.

В математической теории систем системы параметризованы, их состояния координатизированы, то есть задаются наборами числовых значений параметров — точками соответствующих фазовых пространств.

В философском плане симметрия означает неизменность, сохранность структуры объекта при некоторых его преобразованиях. В математике создан мощный аппарат теории групп, позволяющий успешно исследовать явление симметрии в естествознании и искусстве. Абстрактное понятие группы отражает возможность самосовмещений объекта, служит мерой его симметричности. Любой математический объект можно изучать с помощью группы всех его автоморфизмов. Так, геометрической фигуре обычного пространства сопоставляется группа его самосовмещений. Мы видим, что категория симметрии тесно связана с категориями сохранения и тождества.

В математике сохранение, или инвариантность, трактуется как отображение однотипных математических структур, сохраняющее все отношения данной сигнатуры. В общем виде такие отображения называются гомоморфизмами. К ним относятся гомоморфизмы групп, линейные отображения векторных пространств, движения (изометрии), аффинные и проективные преобразования, изотонные отображения упорядоченных множеств, непрерывные отображения топологических пространств. Заметим, что в [131] предложена концепция моделирования — как отражения действительности — на основе понятия гомоморфизма. Тождество — это одинаковость, равенство по определенному признаку, эквивалентность, изоморфность. Изоморфные объекты в абстрактной математике не различаются, тождественны друг другу.

Конечное и бесконечное — фундаментальные философские и общенаучные понятия. Они тесно связаны с такими важнейшими понятиями, как ограниченное и неограниченное. На практике мы имеем дело с конечным: жизнь индивида конечна (ограниченна), мы оперируем только рациональными числами, любая наша деятельность есть конечная последовательность отдельных действий, даже Солнечная система состоит из конечного (пусть и очень большого) числа атомов. Окружающие нас вещи ограничены по своим размерам, и их число конечно. Наше физическое пространство, понимаемое по Ньютону (ящик без стенок, без дна и крышки), бесконечно и неограниченно.

В математике говорят о конечных и бесконечных множествах. Множество называется конечным по Дедекинду, если оно не равномощно никакому своему собственному подмножеству. Напомним, что равномощность (эквивалентность) двух множеств означает, что между ними существует взаимно однозначное соответствие. Естественно, множество называется бесконечным, если оно не является конечным. Кардинальные числа (мощности) и ординальные (порядковые) числа введены Кантором как неотъемлемая составная часть теории множеств. Заметим, что представители интуиционизма не признают бесконечных множеств (актуальную бесконечность); для них возможна лишь становящаяся, потенциальная бесконечность (постепенное продвижение по натуральному ряду). Подавляющее большинство математиков признают, что без понятия бесконечности нет математики.

Категории дискретное и непрерывное многосторонне отражены в современной математике. Существуют понятия: дискретное пространство, дискретная величина, дискретная математика. В дискретной математике, называемой еще конечной математикой, изучаются, главным образом, конечные математические структуры. Конечная математика все больше становится компьютерной математикой. Можно говорить и о непрерывной математике, в которой господствуют идеи предельного перехода и непрерывности.

Математическую часто подразделяют на фундаментальную и прикладную составляющие. Такое деление условно и не очень-то правомерно. Считается, что фундаментальная математика создает и исследует абстрактные математические структуры, следуя внутренней логике своего развития, а прикладная математика имеет дело с математическими моделями реальности. Задачи и теории фундаментальной и прикладной математики различаются только способом своего возникновения — из самой математики, или из практики. Фундаментальная и прикладная математики — это единая теоретическая, фундаментальная, чистая математика. Помимо математики как таковой существуют приложения математики в предметных областях науки и практики (в физике, химии, биологии, экономике, социологии, технике, производстве и т. д.).

Чистая математика подразделяется на содержательную математику, формальную математику и метаматематику. Почти вся классическая математика излагается содержательно-аксиоматически. Формальная математика изучает формальные математические теории, при этом формально аксиоматизируется и логика рассуждений. Метаматематика исследует свойства и интерпретации формальных математических систем.

В математике можно также (в определенной мере условно) выделить непрерывную и дискретную математики, которые друг без друга не обходятся. Непрерывная математика оперирует идеями и понятиями непрерывности, предела, актуальной бесконечности, континуума и воплощается в математическом анализе, топологии, классических геометриях. Дискретная математика (называемая еще конечной математикой) имеет дело с конечными последовательностями вполне определенных действий, вычислений, преобразований. Дискретная математика включает в себя конструктивную математику, объемлющую в свою очередь компьютерную математику. Заметим, что в последнее время все чаще дискретная математика отождествляется с компьютерной математикой. Теоретически компьютерная математика является частью формальной математики.

Укажем теперь более конкретные, специфические положения, утверждающие единство математики.

Во-первых, вся математика пронизана такими основополагающими понятиями, как доказательство и функция. Доказательство есть отражение причинно-следственных связей в логической, дедуктивной форме. Некоторые считают даже, что «математика — это доказательство». А понятие функции математически отражает категорию движения. Математические науки условно делятся по методам доказательств и видам изучаемых ими функций, а стало быть, имеют общую методологическую почву. Так, алгебра изучает алгебраические операции, геометрия — геометрические преобразования фигур, математический анализ — свойства числовых функций, теория вероятностей — вероятностную меру и т. д. Такие важнейшие математические понятия, как производная, интеграл, мера, гомоморфизм (в самом широком смысле), суть функции.

Во-вторых, все математические дисциплины базируются на строгой логике, используют единый символический язык.

В-третьих, объединяющим современную математику началом является фундаментальное понятие математической структуры, понимаемой как множество с заданными на нем отношениями. Н. Бурбаки определили математику как учение о математических структурах. Ими было выделено три основных типа математических структур: алгебраический, порядковый и топологический [65]. Кроме указанных типов математических структур можно также отметить пространства с мерой, формализующие понятие величины, и структуры инцидентности, включающие различные геометрии и теорию графов.

Алгебраическая, порядковая и топологическая структуры теснейшим образом связаны друг с другом. Известные теоремы Г. Биркгофа и П. С. Александрова утверждают, что для конечных структур существуют естественные взаимно однозначные соответствия между дистрибутивными решетками (алгебра), упорядоченными множествами (порядки) и Г₀-пространствами (топология). Структуры инцидентности взаимосвязаны как с алгеброй, так и с геометрией. Большинство конкретных математических объектов является переплетением двух или более типов структур, согласованных между собой. Поэтому в математике так много синтезированных дисциплин, начиная с геометрической алгебры древних греков, тригонометрии и аналитической геометрии (метод координат), вплоть до современных алгебраической геометрии, алгебраической топологии, топологической алгебры, дифференциальной геометрии, дифференциальной алгебры, вероятностной теории чисел и т. п.

Далее, класс всевозможных математических структур фиксированной сигнатуры образует категорию. Между данными объектами существуют морфизмы, сохраняющие их структуру. В алгебре это гомоморфизмы, для упорядоченных множеств — изотопные отображения, в топологии — непрерывные отображения. Среди морфизмов пар объектов выделяются изоморфизмы, фактически отождествляющие эти объекты. Появившаяся в середине XX века теория категорий также является общим языком современной математики.

Как уже было сказано (см. [153]), теоретико-множественный и теоретико-категорный языки равносильны, то есть имеют равные выразительные возможности. Но они принципиально отличаются своим подходом к исследованию математических объектов. Математические структуры изучают внутреннее строение объектов: их элементы, отношения между элементами, подобъекты. А теория категорий изучает объекты через их связи (морфизмы), то есть внешним образом. Оказывается, внутренний анализ любого математического объекта эквивалентен внешнему его рассмотрению как члена сообщества родственных объектов. Это, а также многочисленные теоремы строения, двойственности (например, двойственности Понтрягина, Стоуна, Гельфанда, Хьюитта, Пристли), характеризации, определяемости еще раз указывают на единство математики.

От формы к формуле

Пифагорейский тезис «Все есть натуральное число» можно заменить метафорой «Все есть форма», имеющей глубокий смысл. Такое почтение к форме восходит к Аристотелю. Человеческое познание представляет собой становящийся ряд образов или форм, сменяющих, отражающих и моделирующих друг друга. За одной формой следует другая, казавшаяся до этого содержанием первой. И так далее. Искомая абсолютная истина снова ускользает, скрываясь за чередой образов, облачаясь в новые одежды. Но на каждом этапе познания при смене форм происходит некое откровение, обретение относительной истины, решающей ту или иную задачу. Человеческое познание не слепо, оно следует путем целесообразности, красоты. В научном познании побеждают совершенные, четко очерченные формы.

Согласно Канту, любой умопостигаемый объект познания есть «вещь в себе» (то есть ноумен, в противовес эмпирически познаваемым явлениям — феноменам), которая может быть исследована и описана одним только внешним образом, по принципу «воздействие — реакция», или «вход — выход». Таков и математический подход к изучению действительности, составляющий фундаментальный принцип математизации научного знания. Ведущими в познании выступают категории формы и количества, посредством чего мы и оказываемся в состоянии сказать нечто о содержании, качестве и сущности. Хотя в философии форма традиционно определяется как способ существования содержания, тем не менее, именно она служит творческим началом Мироздания и, соответственно, процесса познания. Всякое «содержание» как-то сформировано и оформлено. Каждое «качество» имеет свои количественные характеристики (меру инвариантности), в пределах возможного изменения которых оно и идентифицируется. Любая «сущность», так или иначе, является, оставляя нам запечатленные данные о себе. А наука занимается сбором и изучением таких анкет.

Мы сосредоточим свое внимание на проявлениях формы в математике. Отметим, что к категории формы относятся абстракции схемы и структуры, отлично «чувствующие себя» в математике. Наглядно форма выражается, прежде всего, в геометрии. Принцип гармонии, или целесообразного отбора, позволяет выделить наиболее изящные и совершенные геометрические фигуры, сделав их предметом пристального изучения. Так же прекрасны начертания замечательных математических формул.

Среди производных от слова «форма» нас интересуют такие важнейшие термины, как формализация и формула. Под формулой понимается записанное на символическом логико-математическом языке математическое предложение или правило. А формализация — это моделирование, заключающееся в переводе информации с обычного языка на язык формул. При этом формула выступает как воплощенная форма в математике, несущая концентрированную мысль. Это один из важнейших способов кодирования и передачи информации, наиболее лаконичный и точный, при котором не происходит объективного ее искажения. Скажем, равенство A=[0,l]x[0, l] тут же воспроизводится нами как единичный квадрат А.

Роль математических формул выразительно подчеркнул физик Генрих Герц: «Трудно избежать чувства, что эти математические формулы ведут независимое существование и имеют свой собственный интеллект, что они мудрее нас, мудрее даже своих создателей, что мы извлекаем из них больше, чем вначале было в них вложено».

В формуле одинаково важны и синтаксис (ее формальное строение), и семантика (возможные интерпретации, смыслы). Имея перед собой формулу, мы фактически можем подразумевать (находить) все ее интерпретации. В формулах происходит диалектическое соединение ипостасей формы и количества. Важнейшую роль играет символика. Математические знаки, обозначения и термины исторически совершенствуются. Математические суждения желательно представить в наиболее простом и ясном виде. Поэтому сложные формулы мы стремимся преобразовать, привести к более простой форме; на этом пути появляются канонические формы для различных классов формул. Установление эквивалентности двух формул служит одним из основных типов теорем в математике.

Говоря о содержательных формулах, следует начать с формул элементарной математики. Основное тригонометрическое тождество, являясь числовым тождеством, служит прекрасным примером функционального равенства. Уместно вспомнить также другие тригонометрические соотношения, свойства степеней, формулы сумм арифметической и геометрической прогрессий, выражения для длин, площадей и объемов в элементарной геометрии, бином Ньютона, формулы Виета, неравенство Коши. Многие элементарные формулы имеют геометрическую интерпретацию, допускают наглядное изображение в виде чертежа или схемы. Например, вспоминается иллюстрация известной формулы 1 + 3 + 5 +… + (2п -1) = п²: ¹

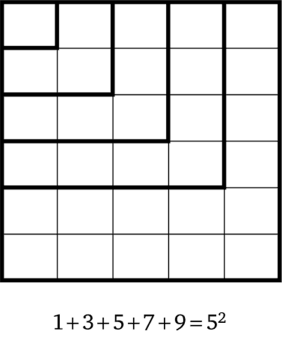
Равенства имеют, как правило, не единственное смысловое значение. Отношение равенства, являясь симметричным в строго математическом смысле, не является таковым при смысловом прочтении формулы. Уже равенства 2 + 2 = 4и4 = 2 + 2 суть не одно и то же. Замечательная формула е^т = -1 означает, что комплекснозначная функция f (z) = e^z при значении z = ni принимает значение -1. А формула -1 = е^т — это представление числа -1 в показательной форме. И, наконец, эта формула отражает единство мира: в ней удивительным образом оказались соединены четыре константы -1 (это, говоря условно, арифметика), п (геометрия), i (алгебра) и е (анализ), появление которых исторически произошло независимо друг от друга.

Особую роль играют формулы-определения. К ним относятся фор;

( 1X

мула второго замечательного предела liml 1 н— I =е, которая служит п—><�".

определением числа е, основное логарифмическое тождество а^1о^^ь = Ъ, являющееся определением логарифма числа b по основанию а, определение производной функции в точке и т. д.

Человек постоянно сталкивается с различными финансовыми вычислениями и расчетами, т. е. с числовыми равенствами. Можно привести восхитительные формулы для чисел е и п:

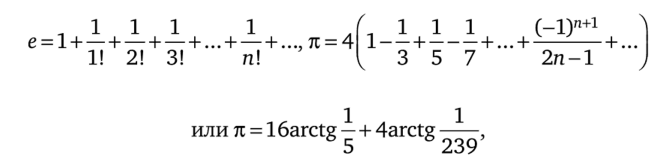
1 + V5 ,.

представление золотого сечения —-— в виде бесконечной цепной дроби, содержащей одни единицы. Следующее равенство, полученное американцем Элкисом с помощью компьютера в 1988 году, дает оптимальный контрпример к известной гипотезе Эйлера (см. [491]):

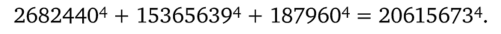
Формальная математика — это символическая формульная математика. На первый план выдвигаются логико-математический язык, его грамматика, логическая форма. Фактически всю математику можно строго формализовать, выразить как формальную аксиоматическую систему. При этом, как правило, появляются новые интерпретации и модели. Так, содержательная аксиоматическая теория Пеано натурального ряда категорична, а формальная теория натуральных чисел имеет модели любой бесконечной мощности. В формальной математике, хотя и происходит некоторый «неадекватный» отход от стандартных моделей, возникает новое знание, расширяются логические и философские представления о возможностях научного описания Мира (вспомним теоремы Геделя).

Законы логики (тавтологии, равносильности, правила вывода) являются таковыми благодаря только своей структуре, синтаксису, вне зависимости от конкретных интерпретаций.

Разработка методов формализации в рамках математической логики послужила основой создания искусственных языков, различных языков программирования, компьютерной алгебры. Практическим венцом такого развития стал современный компьютер.

Исключительную роль в математике играют формулы, записанные в виде равенства термов t₁ = t₂. Будем считать, что мы рассматриваем математическую структуру М, являющуюся моделью некоторой теории. Если термы t₁ и t₂ замкнуты, т. е. обозначают элементы из М, то их равенство есть конкретное высказывание (истинное или ложное). Если же хотя бы один из данных термов содержит переменную, то получаем уравнение, которое желательно решить в М, или тождество t₁(x₁,…, х_п) = t₂(x 1,…, х_п), обращающееся в верное равенство при любых значениях из множества М всех входящих в термы переменных х_г,…, х_п. Заметим, говоря формально, что тождество можно считать частным случаем уравнения, когда множество его решений совпадает с М^п, а верное конкретное равенство в М — тождеством без переменных.

Укажем также, что к миру формул принадлежат многочисленные дифференциальные и интегральные уравнения, а также их решения. Соответствующие разделы математики находят широкое применение в естествознании, поскольку развитые в них методы способны адекватно описывать различные природные процессы. Любая аналитически записанная функция/от аргумента х дает формулу у = f (x).

От тождеств перейдем к понятию гомоморфизма. В общенаучном плане гомоморфизмом называется преобразование родственных объектов, сохраняющее их структуру (от первого объекта ко второму). Более тесную связь объектов обеспечивает наличие изоморфизма между ними (структура сохраняется в обе стороны). Изоморфные объекты структурно не различаются, являясь копиями друг друга (так, десятирублевые купюра и монета изоморфны в денежном отношении).

В математике гомоморфизмы / удовлетворяют специальным «обобщенным тождествам», выражающим перестановочность / со структурными операциями и отношениями. Пусть даны однотипные математические структуры М и N с одним и тем же списком П операций и отношений. В принципе можно рассматривать бесконечноместные отношения и частичные операции. Тогда функция/из М в N называется гомоморфизмом этих математических структур, если для всякого индексного множества I, для любых /-местных операции w и предиката Р из П и для произвольного семейства (т= (m_i)_ie_l элементов в М:

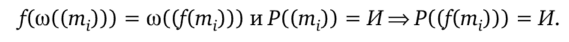
Для алгебраических, порядковых и топологических структур получаем понятия обычного гомоморфизма, изотонного отображения и непрерывного отображения соответственно. Скажем, если М, N — мультипликативные группы, то для гомоморфизма / из М в N тождественно Дш^г) = /(тД х /(т₂). Если М, N — упорядоченные множества с одинаково обозначаемыми отношениями порядка <, то гомоморфность/означает изотонность, т. е. выполнение квазитождества т₁ < т₂ =^>/(mj) < /(m₂). Если же М, N — топологические пространства, то гомоморфность / трактуется следующим образом: для любой сходящейся направленности (гщ) в М имеемДНш т₍) = Нт Дт,), что равносильно непрерывности отображения/.

Как и понятие гомоморфизма, в терминах перестановочности операций формулируются основные свойства многих математических объектов. Назовем, например, законы дистрибутивности и де Моргана, аддитивность производной и интеграла, свойства предельного перехода.

Литература: [62, 65, 66, 88, 131, 134, 153, 491].