Современные расчетные методы дозиметрии в РНД

Наибольшее распространение для расчета доз при внутреннем облучение получили в настоящее время метод MIRD и метод ICRP. Метод ICRP предназначен в основном для использования в профессиональной деятельности в области ядерного топливного цикла, поэтому ограничимся в данном разделе обсуждением только метода MIRD.

Источники данных

Все методы расчета во внутренней радиационной дозиметрии в качестве входных данных требуют знания радиационных характеристик назначаемых р/н, анатомии, в которой производится расчет, и, наконец, биокинетики РФП.

Радиационные характеристики, необходимые при расчетах доз, включают:

• • схемы радиоактивного распада ядер (тип распада, выход эмиссии, энергия излучения, период полураспада);
• • коэффициенты (поперечные сечения) взаимодействия испускаемых излучений с веществом.

Данные по схемам радиоактивного распада ядер не являются статичными, они непрерывно пересматриваются и уточняются, поэтому их новые версии нужно отслеживать в научной литературе. Как правило, эти уточнения не сильно сказываются на финальной точности расчетов доз в ЯМ, так как неопределенности в других используемых данных, особенно в биологических, бывают значительно выше. Уточнения в коэффициентах взаимодействия обычно связаны с совершенствованием теоретических представлений и редко существенно сказываются на погрешностях расчета.

Как отмечалось выше, для проведения расчетов доз, получаемых внутренними органами и тканями, во входные данные необходимо включить также анатомические и радиобиологические данные. Для низкодозовой РНД обычно бывает достаточно анатомических данных для Стандартного (референсного, англ, reference) Человека, данных этнической, половой и возрастной групп, представленных в соответствующих антропоморфных фантомах. Эти фантомы описываются ниже.

Метод МИШ

Подход комитета MIRD к оценке поглощенных доз, получаемых тканью или органом от активности, содержащейся в самом или в другом органе, был впервые опубликовании в 1968 г. [13]. Вслед за этой работой последовали уточняющие и обобщающие публикации [31,32]. В своей первоначальной форме MIRD уравнение имеет замечательно простую форму и определяет поглощенную дозу в области мишени г_т за время t, создаваемую активностью, содержащейся в области источника r_s:

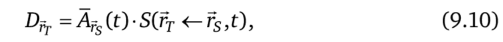
где А_? — полное число ядерных распадов, которое имело место в области источника за время t, известное как кумулятивная активность; S (r_T <�— r_s, t) — величина, которая связывает поглощенную дозу в области мишени за время t с кумулятивной активностью в области источника и известна как S-фактор. Другими словами S-фактор представляет собой среднюю поглощенную дозу в области мишени на единицу кумулятивной активности в области источника за время t.

В практической ядерной медицине S-факторы предварительно рассчитываются для разных комбинаций г_т и r_s. Временные зависимости поглощенной дозы, кумулятивной активности и S-фактора допускаются в схеме MIRD, так же как и вариации объема и морфологии некоторых источников во времени. Двумя наглядными примерами являются мочевой пузырь, который при заполнении мочей раздувается, а при опорожнении, наоборот, сжимается, и опухоли, которые могут увеличиваться в размере (при неудачной терапии) или уменьшаться в результате терапии. Таким образом, геометрия задачи в этих примерах изменяется во времени.

В схеме MIRD опытным путем необходимо только измерить кумулятивную активность A_f в области источника и использовать рассчитанный S-фактор для определения ее вклада в поглощенную дозу, получаемую областью мишени. Вместе с тем, надо понимать, что за простотой уравнения (9.10) скрывается большое количество физических деталей. Эти детали будут представлены через их вывод для области источника r_sи области мишени г_т(рис. 9.2).

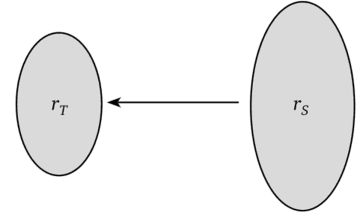
Рис. 9.2. К определению 5-фактора в схеме MIRD.

Области источника и мишени могут совпадать между собой, тогда S-фактор учитывает, фактически, самопоглощение излучения в источнике. Доля энергии, освобождаемой при радиоактивном распаде в r_s и представляющей либо энергию фотонов, либо энергию заряженных частиц, поглощается в области мишени г_т. Следовательно, мощность поглощенной дозы вблизи г_г в момент времени t, обусловленная активностью А_?8 в r_s равна.

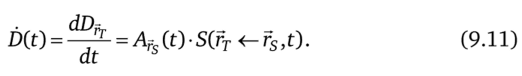
Повторим, что S-фактор представляет собой часть энергии, освобождаемой (испускаемой) при единичном радиоактивном распаде в области источника, которая поглощается в области мишени, нормализованной на массу области мишени тп^. Из-за зависимости от расстояния, разделяющего r_s, г_т, и массы m^ S-фактор является для данного р/н функцией половых и возрастных размеров и расстояния между областями источника и мишени. В схеме MIRD они определяются как специфические органы, ткани или содержание органов, хотя нет особого смысла ограничивать предопределенные органы источника и мишени. Например, схема может быть применена к воксельным фантомам, в которых распределение активности и поглощенной дозы оценивается для индивидуальных вокселей, определенным из томографических визуализационных данных.

Полная поглощенная доза в г_т равна интегралу от мощности поглощенной дозы, даваемой формулой (9.17), по времени облучения Техр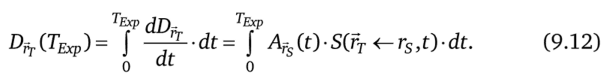

При расчетах в РНД значение Т_Ехр устанавливается обычно Т^ = оо, в то время как в расчетах по радиационной безопасности для профессионалов эта величина берется равной Техр = 50 лет. На практике область мишени облучается несколькими районами источников, поэтому уравнение (9.12) следует переписать в виде суммы по всем]У₅ районам источников.

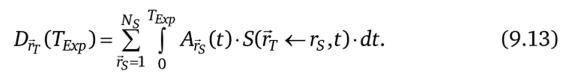
Из определения S-фактора можно написать следующую расчетную формулу:

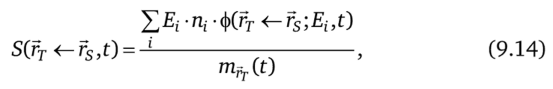
где суммирование ведется по всем каналам распада ядра; m^ (t) —масса объема мишени в момент времени t; ф (г_т <�— r_s;E_ht) — поглощенная доля энергии Ej, которая испускается в момент времени t из области источника r_sи поглощается в объеме мишени г_т.

В табл. 9.3, в качестве примера приводятся значения S-факторов для р/н «^тТс для разных комбинаций областей мишени и источника, взятые из публикации комитета MIRD 1975 г. [33]. Данные в этой работе получены для широкого круга р/н с помощью расчета методом МонтеКарло для типовых антропоморфных фантомов. Хорошая компиляция результатов последних расчетов S-фактора выполнена Стабином в работе [34].

Значения 5-фактора в единицах средней поглощенной дозы на единицу кумулятивной активности (радДмкКи • ч)) для 99тТс [33]. Для перевода в единицы СИ (ГрДМБк • ч)) необходимо данные в табл. 9.3 поделить на 3,7.

Таблица 9.3

Окончание табл. 1.2

Стабин и Зигель в работе [35] расширили определение S-фактора, включив в него радиационный взвешивающий фактор из ICRP Публикации 26 [1] для наиболее значимых продуктов радиоактивного распада:

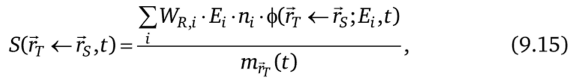
Уравнение (9.14) для S-фактора нередко записывается в упрощенной форме.

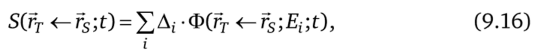
где, А 1=п₍-Е_{ — средняя энергия, испускаемая при каждом распаде по i-каналу;

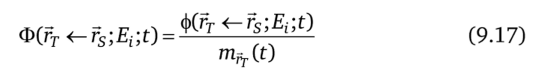
называется удельной поглощенной долей (фракцией) и определяется как поглощенная доля на единицу массы объема мишени.

Выражение (9.15) для р/н, испускающих (3-частицы с непрерывным спектром, удобно записать в непрерывной форме:

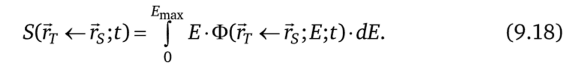
Комбинируя уравнения (9.19), (9.23), (9.24) и устремляя время облучения к бесконечности, получаем следующее уравнение для поглощенной дозы в мишени:

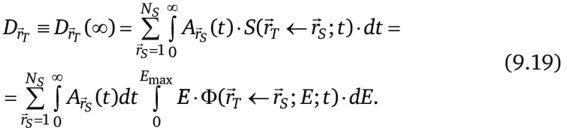
Выражение (9.19) является наиболее общей формой уравнения для расчета поглощенной дозы в области мишени с учетом временных изменений в морфологии и размерах органов. На практике удельную поглощенную долю считают постоянной во времени, и тогда уравнение (9.19) записывается в следующем виде:

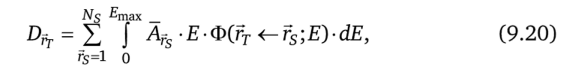
где А_?5 = J*Ap_s(t)-dt — кумулятивная активность. Отметим, что кумулятивная активность является безразмерной величиной, так как определяется как произведение активности (время^-1) на время.