Оптимальный фильтр Калмана — Бьюси

С помощью теории фильтрации Калмана — Бьюси удается устранить ограниченность применения метода Винера. Она позволяет решать задачи синтеза как для установившегося, так и для переходного режимов. В установившемся режиме оптимальные решения задач на основе фильтров Винера и Калмана — Бьюси совпадают. Оптимальную линейную фильтрацию Калмана — Бьюси можно рассматривать как дальнейшее развитие метода Винера, основанное на понятии «состояние динамической системы». Как известно [9], метод уравнений пространства состояний позволяет выработать общий подход к анализу многомерных динамических систем без дополнительных теоретических усложнений.

Основные соотношения, определяющие метод нестационарной непрерывной фильтрации Калмана — Бьюси, получены с помощью дифференциальных уравнений или уравнений состояния, которые описывают случайные процессы в динамической системе. Калман и Бьюси показали, что при случайных воздействиях оптимальная линейная система (оптимальный фильтр Калмана — Бьюси) должна удовлетворять некоторой системе дифференциальных уравнений.

Ниже рассматривается основная идея метода Калмана — Бьюси. Для простоты считается, что система одномерная. На входе системы автоматического управления действует сигнал g (t), равный сумме задающего x (t) =y_np{t) и возмущающего/(t) воздействий: g (t) = xr (t) +/(t), которые являются нестационарными случайными процессами. Кроме этого предполагается, что возмущающее воздействие представляет собой случайный процесс типа «белого шума» с нулевым математическим ожиданием, а задающее воздействие x (t) может быть представлено следующим дифференциальным уравнением:

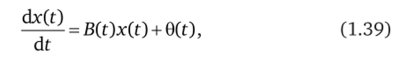
где B (t) — функция времени, зависящая от статистически характеристик случайного процесса x (t); 0(t) — нестационарный случайный процесс типа «белого шума» с математическим ожиданием, равным нулю.

Уравнение (1.39) описывает работу некоторого формирующего фильтра, на входе которого сигнал 0(f), а на выходе — x (t).

Корреляционные функции случайных процессов/(f) и 0(f) [17]: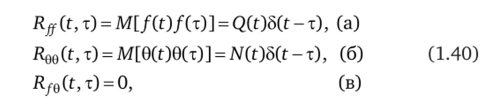

где функции Q (f) и JV (f), характеризующие интенсивности шумов/(0 и 0(0, — непрерывные положительно определенные функции, имеющие непрерывные производные. Ошибка системы z (0 равна разности между желаемым (воспроизводимым) значением х (0 = У_ПрЮ ^и выходным сигналом у (0:

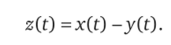
Калман и Бьюси показали [4, 17], что оптимальная система (оптимальный фильтр Калмана — Бьюси), обеспечивающая минимальное значение средней квадратической ошибки z2_K(0 = [x (t)-y (t)]² =е (0, должна удовлетворять следующему уравнению:

где С (0 и D (t) — некоторые функции времени, определяемые на основе выражений.

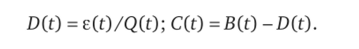
Функция e (t), соответствующая средней квадратической ошибке, определяется как решение следующего дифференциального уравнения Риккати:

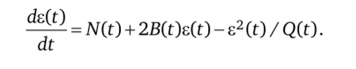
С учетом выражения для функции C (t) уравнение оптимального фильтра Калмана — Бьюси иногда записывают в следующем виде:

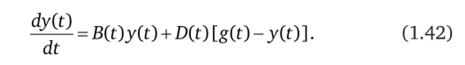
На рис. 1.18 приведены структурные схемы оптимального фильтра Калмана — Бьюси, соответствующие дифференциальным уравнениям (1.41) и (1.42).

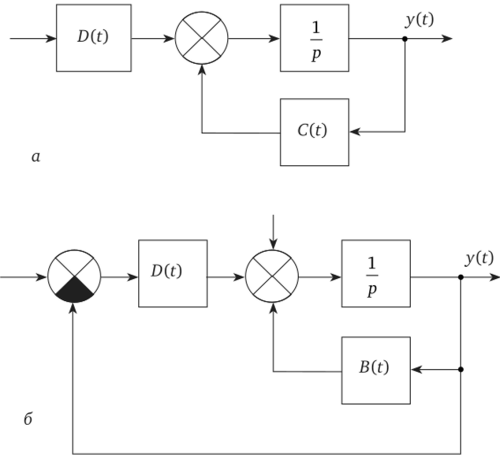
Рис. 1.18. Разновидности фильтра Кальмана — Бьюси.

Системы автоматического управления, представленные структурными схемами на рис. 1.18, воспроизводят на своем выходе случайный сигнал у(t) с минимальной средней квадратической ошибкой.

Следует отметить, что для нестационарных случайных процессов функции B (t), C (t) и D (t) зависят от времени и оптимальный фильтр Калмана — Бьюси является нестационарным.

Естественно, что для стационарных случайных функции В (f) = = В = const, а также в установившемся режиме функции D (t) = = D = const и C (t) — С = В — D — const, т. е. не зависят от времени.

Для того чтобы случайный процесс x (t) представить в виде уравнения (1.39), необходимо на входе некоторого формирующего фильтра с передаточной функцией 17ф (р) действие сигнала типа «белого шума» 0(f) — Особенно просто параметры формирующего фильтра определяются для стационарных случайных процессов, когда спектральная плотность задающего воздействия x (t) имеет вид дробно-рациональной функции. В этом случае спектральная плотность может быть представлена в виде произведения двух комплексно-сопряженных сомножителей [17]:

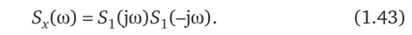
При действии на входе формирующего фильтра сигнала 0(0 с характеристиками (1.40а) спектральная плотность выходного сигнала x (t).

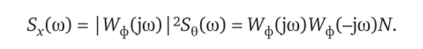
С учетом соотношения (1.43) последнее выражение примет вид.

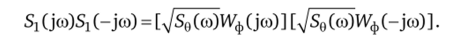
Отсюда получаем комплексный коэффициент усиления и передаточную функцию формирующего фильтра:

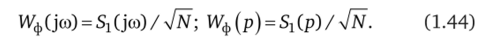
На основе (1.44) определяется дифференциальное уравнение вида (1.39).

С помощью метода Калмана — Бьюси можно также сравнительно просто найти структуру и параметры оптимального фильтра, когда задающий (желаемый) сигнал х (?) представляет собой полином с коэффициентами bj, которые являются случайными величинами с известными статистическими характеристиками:

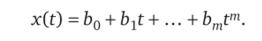
В заключение следует отметить, что методика Калмана — Бьюси в последующем была развита для более общих случаев (коррелированные воздействия, неравномерные спектральные плотности и т. д.).