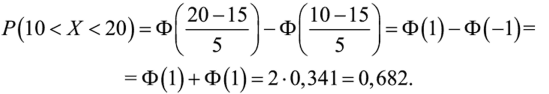Законы распределения непрерывной случайной величины

Во многих практических задачах приходится сталкиваться с определенными законами распределения непрерывных случайных величин. Часто встречаются законы равномерного, нормального, показательного распределения вероятностей.

Равномерный закон распределения

Встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (плотность вероятности).

Функция распределения (рис. 6).

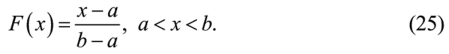
Плотность вероятности (рис. 6).

Математическое ожидание и дисперсия вычисляются по приведенным ниже формулам: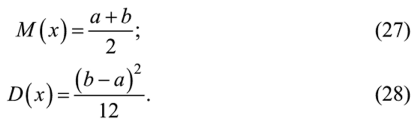

Равномерному закону распределения подчиняются, например, погрешности округления, возникающие в результате отбрасывания у чисел одной или нескольких цифр. С этим довольно часто приходится встречаться экспериментаторам в различных областях измерительной практики. Данное свойство используется в некоторых генераторах псевдослучайных чисел [21].

Равномерному закону подчиняются случайные погрешности, например, от трения в опорах стрелочных приборов, от квантования по значению в цифровых приборах и ряд других [22].

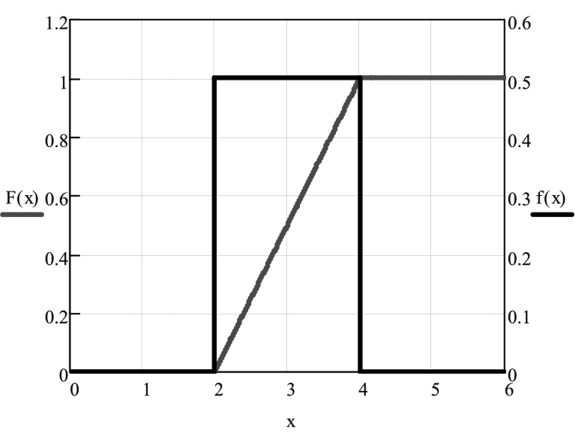
Рис. 6. Графики функции распределения F (x) и плотности вероятности f (x)

при, а — 2, b = 4.

Нормальный закон распределения

Нормальный закон распределения называют фундаментальным законом в теории вероятности, т. к. его применение часто встречается при изучении природных и социально-экономических явлений.

Особенность закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.

Распределение плотности вероятности случайной величины называется нормальным, если плотность вероятности описывается функцией следующего вида (рис. 7):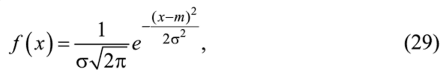

где т — математическое ожидание, мода, медиана; а — стандартное отклонение.

Функция распределения (рис. 7).

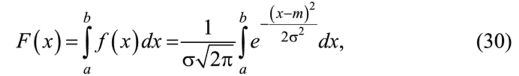
где а и Ь- пределы изменения значений случайной величины X.

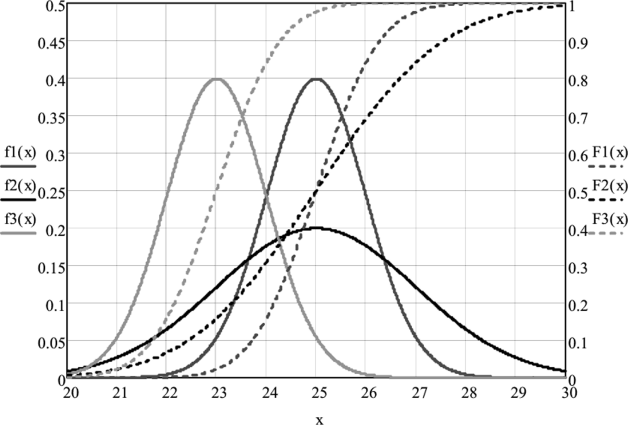
Рис. 6а. Графики функции распределения Г (х) и плотности вероятности /(х): т-1, a=l (/l (x), /П (х)); т-25, a=2(/2(x),, F2(x));

т = 23, a = l (/3(x), F3(x)).

Вероятность попадания случайной непрерывной величины X в заданный интервал [а, Ъ].

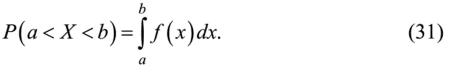
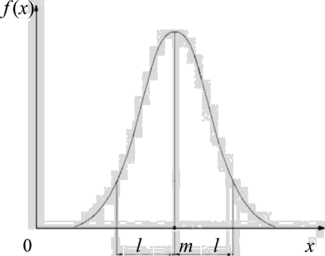
Рис. 7. График плотности распределения случайной величины X

Математическое ожидание и дисперсия вычисляются по приведенным формулам:

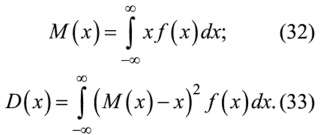
Часто приходится вычислять вероятность того, что значение случайной величины X попадает в интервал (т -1, т + /) (рис. 7).

Вероятность, с которой в условиях данного эксперимента полученные экспериментальные данные можно считать надежными либо достоверными, называют доверительной вероятностью, или надежностью, а интервал хе[-/, +/], соответствующий доверительной вероятности, называется доверительным интервалом.

Вероятность того, что значение случайной величины X попадет в интервал (т-1, т + 1), выраженный через среднеквадратичное отклонение о (/ = ст, 2а, За), приведена в табл. 5.

Таблица 5.

Правило трех сигм

По правилу трех сигм вероятность того, что случайная величина отклонится от своего математического ожидания на величину, большую утроенного среднеквадратичного отклонения, практически равна нулю.

Часто, применяя закон нормального распределения, пользуются понятием функции Лапласа. Для ее получения в выражении (33) производят следующую замену.

следовательно,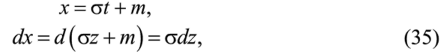

а пределы интегрирования по введенной переменной t, соответственно верхний и нижний:

Подставив (38), (39) и (40) в (34) и проведя преобразования, получим 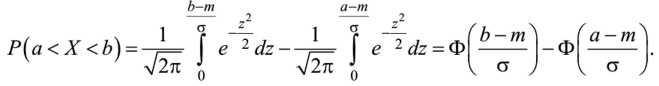Выражение.

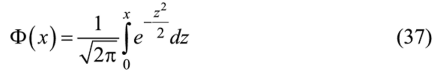
получило название функции Лапласа.

Обычно функция Лапласа используется для вычисления вероятности попадания в заданный интервал нормально распределенной случайной величины X:

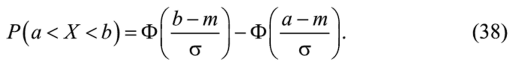
Другими словами, сначала нормализуются величины а и h (40), а затем вычисляется либо определяется по таблице (прил. 1) от них функция Лапласа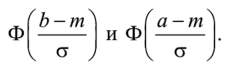

Пример

Найти вероятность того, что случайная величина X, имеющая нормальное распределение с математическим ожиданием т = 15 и среднеквадратичное отклонение, а = 5, примет значение, принадлежащее интервалу [10, 20].

Решение

Вероятность найдем по выражению (38) и прил. 1: