Вывод закона Фурье

Чтобы получить выражение для вектора плотности потока тепла, рассмотрим сначала частный случай, когда температура зависит только от одной пространственной координаты, например, от х:

Очевидно, что в этом случае вектор q плотности потока тепла будет направлен вдоль оси х, т. е. будет иметь только одну отличную от нуля проекцию q_x.

Рис. 5.12.

К выводу закона Фурье

Построим воображаемую плоскость площадью 5, которая перпендикулярна к оси х и пересекает ее в точке х (рис. 5.12). С двух сторон на эту плоскость падают молекулы. За время dt на каждую сторону упадут молекулы, число которых.

Так как по разные стороны от плоскости S газ имеет различные значения температуры Т и То, средние значения энергии одной молекулы в потоках, движущихся навстречу друг другу, будут различны:

Молекулы, движущиеся слева направо, за время dt переносят через плоскость S энергию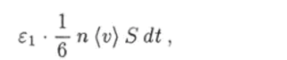

а молекулы, движущиеся в обратном направлении, — энергию.

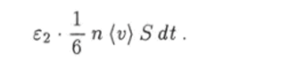
Поэтому, используя определение плотности потока тепла, можно записать равенство.

или Средняя энергия молекулы т, к Т определяется температурой той точки пространства, где она испытала последнее соударение. Для однонаправленного потока молекул эти точки находятся от плоскости S в среднем на расстоянии, равном длине свободного пробега молекулы Л. По этой причине следует положить Так как.

где для плотности потока тепла будем иметь следующее выражение:

При помощи выражений (3.44) и (5.8) для (v) и Л последнюю формулу можно преобразовать к виду.

Формулы (5.51) и (5.52) выражают собой закон Фурье.

Уравнение теплопроводности

Интегральное уравнение (5.33).

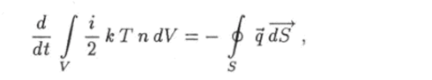
выражающее закон сохранения энергии в процессе переноса тепла, можно преобразовать при помощи теоремы Остроградского — Гаусса в дифференциальное уравнение.

Как видно из этого уравнения, скорость изменения температуры определяется дивергенцией div q вектора плотности потока тепла. Если она равна нулю, то температура со временем не изменяется. Однако температура может изменяться от одной точки пространства к другой. В таком случае распределение температуры называется стационарным.

В общем случае, когда температур распределена в пространстве произвольным образом, закон Фурье выражает формула.

Подстановка выражения (5.54) в равенство (5.53) приводит к уравнению.

В том случае, когда можно пренебречь зависимостью коэффициента теплопроводности от температуры, будем иметь уравнение.

где Д — оператор Лапласа. Это уравнение называется уравнением теплопроводности. Нетрудно видеть, что это уравнение, но форме в точности совпадает с уравнением диффузии (5.46). Уравнение теплопроводности (5.55) справедливо не только для газов, но и для жидких и твердых тел.

Уравнения диффузии и теплопроводности суть уравнения в частных производных и их решение в общем случае является очень сложной задачей. Но стационарные распределения температуры могут быть найдены сравнительно просто ь тех случаях, когда исследуемая система обладает каким-либо типом симметрии. Рассмотрим два примера.

Пример 1. Пространство между двумя плоскостями заполнено веществом, для которого коэффициент теплопроводности к не зависит от температуры. Направим ось х перпендикулярно к этим плоскостям, а начало отсчета поместим на одной из них. Тогда уравнения плоскостей будут иметь вид х = 0 и х = d — расстояние между плоскостями. Если возле каждой из этих плоскостей температура вещества каким-то образом поддерживается постоянной, то распределение температуры между плоскостями со временем примет стационарный характер и будет описываться функцией Т = Т (х). Из уравнения теплопроводности (5.55) вытекает уравнение для этой функции.

Общим решением этого уравнения является функция.

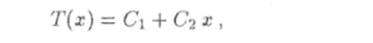
где С и Сч — постоянные интегрирования. Эти постоянные найдем из граничных условий.

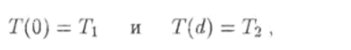
согласно которым в плоскости х — 0 температура равна 7, а в плоскости х = d — То. Граничные условия приводят к уравнениям.

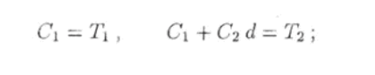
разрешив которые относительно С и Сч найдем частное решение уравнения теплопроводности.

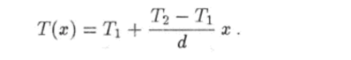
Закон Фурье (5.51) в этом случае будет выглядеть гак:

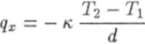
Пример 2. Пространство между двумя концентрическими сферами радиусов, а и 6 заполнено проводящим тепло однородным веществом. Если температура вещества у поверхностей этих сфер поддерживается постоянной, то в силу сферической симметрии системы стационарное распределение температуры в веществе будет описываться функцией.

где г — расстояние от центра сфер до произвольной точки пространства между ними. Введем прямоугольную декартову систему координат, начало которой поместим в центр сфер. При этом.

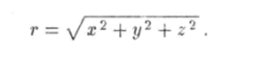
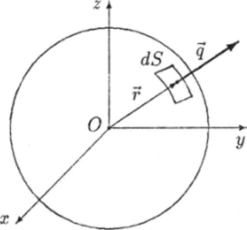
Рис. 5.13. К вычислению потока вектора q.

Подставив функцию (5.56) в формулу (5.54) для закона Фурье, придем к выражению.

которое описывает сферически симметричное векторное поле. Из этой формулы следует, что тепло распространяется по веществу от одной сферы к другой вдоль прямых, идущих из начала координат.

Вычислим поток Q вектора q через поверхность S сферы радиуса г, т. е. количество тепла Q, протекающего через эту сферу за единицу времени: где n — единичный вектор внешней нормали к поверхности. Так как вектор q совпадает, но направлению с вектором п нормали к поверхности сферы, подстановка выражения (5.47) в формулу (5.48) дает.

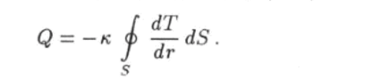
На поверхности сферы г = const и поэтому производная функции (5.56) также постоянна. При этом будем иметь.

Когда тепло протекает через вещество стационарно, в силу закона сохранения энергии через любую замкнутую поверхность, охватывающую сферу меньшего радиуса, за единицу времени протекает одно и то же количество тепла. В частности это означает, что поток тепла через любую сферу не зависит от ее радиуса:

Разрешив равенство (5.59) относительно производной, получим уравнение для функции (5.56):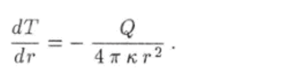

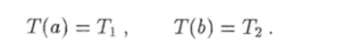
В случае, когда коэффициент теплопроводности не зависит от температуры, это уравнение имеет решение.

где С — постоянная интегрирования. Пусть температура внутренней сферы равна 7ь, а внешней — Т^:

Функция (5.60) будет удовлетворять этим граничным условиям, если.

Радиусы сфер, их температуры и поток тепла могут быть измерены. Поэтому в этих уравнениях неизвестными следует считать постоянную С и коэффициент теплопроводности к. Решив эти уравнения, найдем, что.

где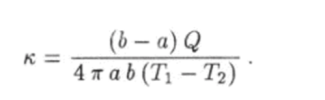

Из формулы (5.58) следует, что поток тепла положителен, когда векторы q и п сонаправлены, т. е. когда тепло распространяется от внутренней сферы к внешней. При этом функция (5.61) является убывающей и Т > Т₂ (рис. 5.14).

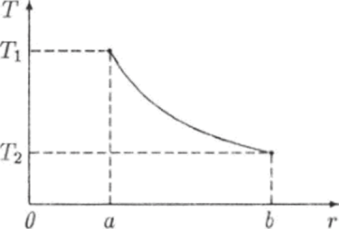
Рис. 5.Ц.

Зависимость Т = Т (г) температуры от расстояния при условии Q > О Если же поток тепла отрицателен, то это означает, что вектор q плотности потока тепла направлен против вектора п внешней нормали, а тепло распространяется от внешней сферы к внутренней. В этом случае функция (5.61) является возрастающей и Т < Т₂ (рис. 5.15).

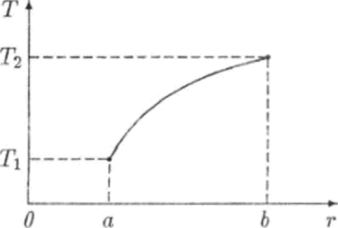
Рис. 5.15.

Зависимость Т = Т (г) температуры от расстояния при условии Q < О.