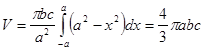Объём тела. 
Применение определенного интеграла для решения прикладных задач

Начнём с почти очевидного замечания: прямой цилиндр высоты H, основанием которого служит квадрируемая плоская фигура (P), имеет объём, равный произведению площади основания на высоту:.

Возьмём многоугольники и, соответственно содержащиеся в (P), так, чтобы их площади и стремились к P. Если на этих многоугольниках построить прямые призмы и высоты H, то их объёмы и будут стремиться к общему пределу, который и будет объёмом нашего цилиндра.

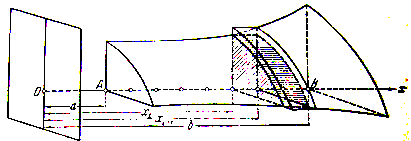
Рассмотрим теперь некоторое тело (V), содержащееся между плоскостями и, и станем рассекать его плоскостями, перпендикулярными к оси x (чертёж 7). Допустим, что (чертёж 7) все эти сечения квадрируемы, и пусть площадь сечения, отвечающего абсциссе x , — обозначим её через P (x) — будет непрерывной функцией от x (для).

Если спроектировать без искажения два подобных сечения на какую-либо плоскость, перпендикулярную к осиx, то они могут либо содержаться одно в другом (чертёж 8а), либо частично одно на другое налегать, (чертёж 8) или лежать одно вне другого (чертёж 8б и 8в). Мы остановимся на том случае, когда два различных сечения, будучи спроектированы на плоскость, перпендикулярную к оси x, оказываются всегда содержащимися одно в другом.

В этом предположении можно утверждать, что тело имеет объём, который выражается формулой.

. (5).

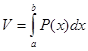
Для доказательства разобьём отрезок на оси x точками на части и разложим плоскостями, проведёнными через точки деления, всё тело на слои. Рассмотрим iй слой, содержащийся между плоскостями и (i = 0,1,…, n -1). В промежутке функция P (x) имеет наибольшее значение и. Если сечения, отвечающие различным значениям x в этом промежутке, поместить на одну плоскость, скажем,, то все они при сделанном предположении будут содержаться в наибольшем, имеющем площадь, и содержать в себе наименьшее, с площадью. Если на этих, наибольшем и наименьшем, сечениях построить прямые цилиндры высоты, то больший из них будет содержать в себе рассматриваемый слой нашего тела, а меньший сам будет содержаться в этом слое. На основании сделанного вначале замечания объёмы этих цилиндров будут, соответственно, и .

Из входящих цилиндров составится тело (T), а из выходящих — тело (U). Их объёмы равны, соответственно, и и, когда стремится к нулю, имеют общий предел (5). Значит таков же будет и объём тела (V).

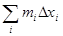
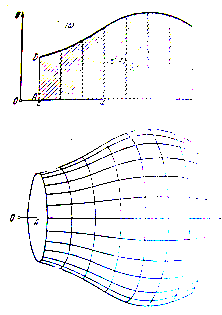
Важный частный случай, когда заведомо выполняется указанное выше предположение о взаимном расположении сечений, представляют тела вращения. Вообразим на плоскости xy кривую, заданную уравнением, где непрерывна и неотрицательна. Станем вращать ограниченную её криволинейную трапецию вокруг оси x (чертёж 9а и 9б). Полученное тело (V), очевидно, подходит под рассматриваемый случай, ибо сечения его проектируются на перпендикулярную к оси x плоскость в виде концентрических кругов. Здесь, так что.

.

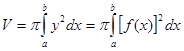
Если криволинейная трапеция ограничена (чертёж 9).

и сверху и снизу кривыми и, то очевидно,.

(7).

Хотя предположение о сечениях здесь может и не выполняться. Вообще доказанный результат легко распространяется на все такие тела, которые получаются путём сложения или вычитания из тел, удовлетворяющих упомянутому предположению.

В общем случае можно утверждать лишь следующее: если тело (V) имеет объём, то он выражается формулой (6).

Примеры: 1). Пусть эллипс вращается вокруг оси x. Так как, то для объёма эллипсоида вращения найдём.

.

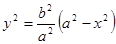
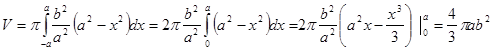
Аналогично для объёма тела, полученного от вращения вокруг оси y, найдём выражение. Предполагая же в этих формулах, мы получим для объёма щара радиуса r известное значение .

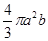
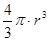
2). То же — для ветви циклоиды, (). Параметрическое уравнение кривой облегчают выполнение подстановки, в формуле. Именно:

.

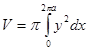
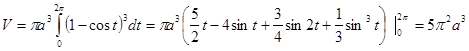
3). Найти объём трёхосного эллипсоида, заданного каноническим уравнением (чертёж 10).

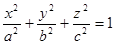
Плоскость, перпендикулярная к оси x и проходящая через точку M (x) на этой оси, пересечёт эллипсоид по эллипсу. Уравнение проекции его (без искажения) на плоскость yz будет таково: (чертёж 10).

(x =const).

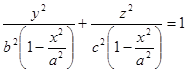
Отсюда ясно, что полуоси его будут, соответственно,.

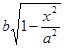
и ,.

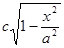
а площадь выразится так:

.

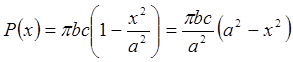
Таким образом, по формуле (5) искомый объём.

.