Расчет реакции связей, вызываемых нагрузками

Задача С1

Жесткая рама, расположенная в вертикальной плоскости, закреплена в точке, А шарнирно неподвижно, а в точке В — к шарнирной опоре на катках.

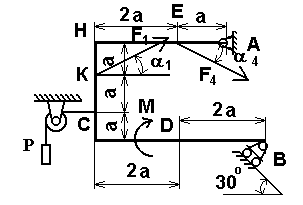
В точке С к раме привязан трос, перекинутый через блок и несущий на конце груз весом Р = 25 кН. На раму действуют пара сил с моментом М = 100 кНм и две силы F₁=20 кН и F₃=30 кН, действующие под углами соответственно ₂=75 и ₄=30.

Определить реакции связей в точках А, В, вызываемые действующими нагрузками. При окончательных расчетах принять, а = 0,5 м.

Дано: Т = Р = 25 кН; М = 100 кНм; F₁=10 кН и F₄=40 кН; ₁=75; ₄=30.

Решение. 1. Рассмотрим равновесие рамы. Проведем координатные оси ху и изобразим действующие на пластину силы: силы F₁, F₃, пару сил с моментом М, натяжение троса Т (по модулю Т = Р) и реакции связей R_АX, R_AY, R_B.

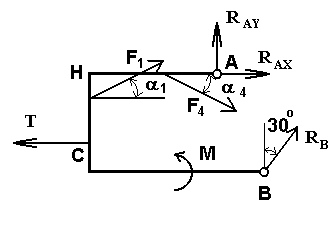
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении моментов сил F1 и F4 относительно точки, А воспользуемся теоремой Вариньона, т. е. разложим силы F1 и F4 на составляющие по осям х и у. Получим:

M_A=0; F₁cos75a + T2a — F₁cos153a + F₄cos60a + R_Bcos603a + R_Bcos302a — M=0;

F_kx=0; R_AX + F₁cos75 — T + F₄cos30 + R_Bcos60=0.

F_ky=0; R_AY + F₁sin75 — F₄sin30 + R_Bsin60=0.

Подставив в составленные уравнения числовые значения заданных величин и решив эти уравнения, определим искомые реакции Ответ: R_B=33,3 кН; R_AX = 40,67 кН; R_AY = -8,04 кН Задача С2.

Конструкция состоит из жесткого угольника и стержня, которые в точке С свободно опираются друг о друга. Внешними связями, наложенными на конструкцию, являются в точке, А и В шарниры, в точке D шарнирная опора на катках.

На конструкцию действуют: пара сил с моментом М = 60 кНм, равномерно распределенная нагрузка интенсивности q = 20 кН/м на участке АЕ и силы F₁=10 кН и F₃=30 кН, действующие под углами соответственно ₁=75 и ₃=60.

Определить реакции связей в точках А, В, С, вызванные заданными нагрузками. При окончательных расчетах принять, а = 0,2 м.

Дано: М = 60 кНм; q = 20 кН/м; F₁=10 кН; F₃=30 кН; ₁=75; ₃=60; а = 0,2 м.

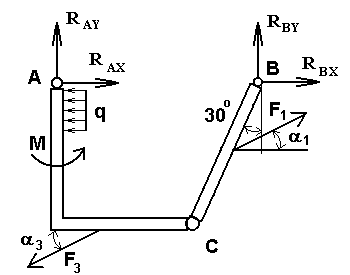
Решение. 1. для определения реакций рассмотрим равновесие всей системы. Проведем координатные ху, изобразим действующие на стержень силы: силу F₂, силу F₄, реакции R_АX; R_АУ, R_ВX; R_ВУ, момент М, распределенную нагрузку q. Для полученной плоской системы сил составляем три уравнения равновесия:

M_А=0; F₃cos608a — М + q3a1,5a — F₁cos15(6a + 6acos60) — F₁cos75(10a — 6acos30) + R_BX(10a — 10acos30) — R_BY (6a + 10acos60)=0;

F_kx=0; F₁cos75 — F₃cos60+ R_BX + R_AX — q4a =0;

F_ky=0; F₁cos15 — F₃cos30 + R_AY + R_BY=0;

2. Теперь расчленим систему и рассмотрим равновесие стержня ВС. На него действует сила давления стержня АС, направленная по осям х и у R_CХ, R_CУ, сила F₂, реакции R_ВX; R_ВУ.

Для этой плоской системы сил тоже составляем три уравнения равновесия:

M_С=0; -F₁cos756a + R_BX10acos30 — R_BY 10acos60=0;

F_kx=0; - F₁cos75+ R_BX + R_СX =0;

F_ky=0; + F₁cos15 + R_СY + R_BY =0;

Ответ: R_СУ = 25,27 кН; R_CХ = 21,61 кН; R_BX= -12,61 кН; R_BY = -42,59 кН; R_AX = -12,03 кН; R_AY = 61,27 кН.

Знак «-» указывает, что силы направлены противоположно показанным на рисунках.

Задача С4.

Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены подпятником в точке А, цилиндрическим шарниром в точке В и невесомым стержнем 1. Все стержни прикреплены к плитам и к неподвижным опорам шарнирами.

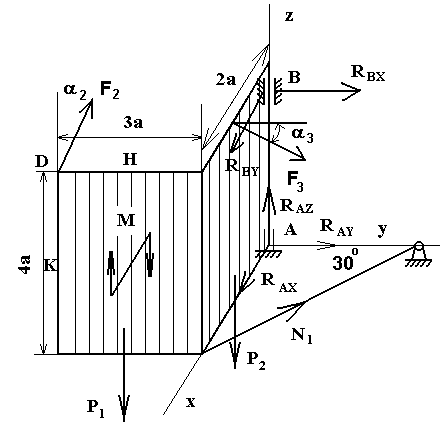
Размеры плит указаны на рисунках; вес большей плиты Р₁ = 5 кН, вес меньшей плиты Р₂ = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость ху — горизонтальная).

На плиты действуют пара сил с моментом М = 4 кНм, лежащая в плоскости одной из плит, и две силы F₂ = 8 кН и F₃=10 кН. Определить реакции связей в точках Л и В и реакцию стержня (стержней). При подсчетах принять а= 0,6 м.

Дано: Р₁ = 5 кН; Р₂ = 3 кН; М = 4 кНм; F₂ = 8 кН; F₃=10 кН; а= 0,6 м, ₂=60; ₃=30.

Решение. 1. Рассмотрим равновесие плиты. На плиту действуют заданные силы: Р₁; Р₂; F₃; F₄ и пара с моментом М, а также реакции связей. Реакцию подпятника разложим на три составляющие R_AX; R_AY, R_AZ, цилиндрического подшипника — на две составляющие R_ВX; R_ВУ, реакцию N стержня направляем вдоль стержня, предполагая, что он растянут.

2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:

Для определения моментов силы F относительно осей разлагаем ее на составляющие F' и F", параллельные осям х и z, и применяем теорему Вариньона. Аналогично можно поступить при определении моментов реакции N.

F_kx=0; R_BX + R_AX — F₂cos30 — N cos60=0.

F_ky=0; N₁ cos30+ R_BY + R_AY + F₃cos30 =0.

F_kz=0; R_AZ — P₁ — P₂ — F₃sin30 + F₂cos60 =0.

M_X=0; -P₁1.5a + F₃cos30 4a + R_BY4a + F₂cos60 3a + M=0;

M_Y=0; P₁2a + P₂a + R_BX4a + F₃cos60a — F₂cos60 2a — F₂cos30 4a =0;

M_Z=0; - N₁2acos30 — F₃sin60a + F₂cos303a =0.

Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.

Ответ: R_AX = -0,97 кН; R_AY =-15,25 кН; R_AZ=16,66 кН; R_BY=14,12 кН; R_BX=-9,48 кН; N₁= -12,12 кН Знак «-» указывает, что силы направлены противоположно показанным на рисунках.

Задача K. Iа Точка В движется в плоскости ху — траектория точки на рисунке показана условно. Закон движения точки задан уравнениями:

.

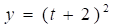
где х и у выражены в сантиметрах, t — в секундах.

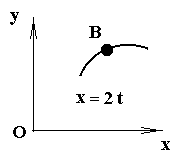
Найти уравнение траектории точки; для момента времени t₁ = 1с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.

Решение К1а.

1. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Выразим t из первого уравнения:

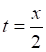
подставим в другое уравнение. Тогда, закон движения точки примет вид:

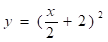
Уравнение движения — парабола.

2. Скорость точки найдем по ее проекциям на координатные оси:

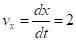
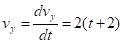
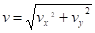
; (1).

и при t₁ = 1 с v_1x=2 см/с, v_1y = 6 см/с; v₁=6,32 см/с.

3. Аналогично найдем ускорение точки:

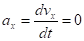
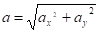
; (2).

и при t₁ =1 с ускорения равны а_x = 0 см/с², a_y = 2 см/с², а₁ = 2 см/с².

4. Касательное ускорение найдем, дифференцируя по времени равенство.

.

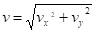
Получим:

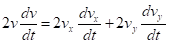
откуда.

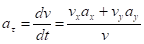
(3).

Числовые значения всех величин, входящих в правую часть выражения (3), определены и даются равенствами (1) и (2). Подставив в (3) эти числа, найдем сразу, что при t₁ = 1 с a₁= 1,89 см/с².

5. Нормальное ускорение точки.

.

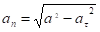
Подставляя сюда найденные числовые значения а₁ и a, получим, что при t₁= 1 a_n= 0,65 см/с².

6. Радиус кривизны траектории.

r= v²/a_n.

Подставляя сюда числовые значения v₁ и а_1n найдем, что при t = 1 с r₁ = 61,4 см.

Ответ: v₁=6.32 см/с, а₁ = 2 см/с², a₁= 1,89 см/с², a_n= 0,65 см/с², r₁ = 61,4 см.

Задача К1б Точка движется по дуге окружности радиуса R = 2 м. по закону.

(s — в метрах, t — в секундах), где s = AM — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности.

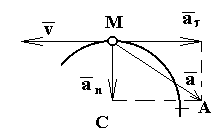
Определить скорость и ускорение точки в момент времени t₁ = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от, А к М.

Решение. Определяем скорость точки:

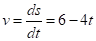
При t = 1 с получим v₁ = 2 м/с.

Ускорение находим по его касательной и нормальной составляющим:

;

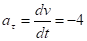
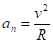
Рис. К2.5

Рис. К2.7

г 1.

Рис. К2.9

При t = 1 с получим, учтя, что R = 2 м., а₁ = -4 м/с², а_n =2 м/с². Тогда ускорение точки при t = 1 с будет.

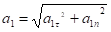
= 4,47 м/с².

Изобразим на рис векторы v₁ и а₁, учитывая знаки v₁ и a₁, и считая положительным направление от, А к М.

Задача К2.

Механизм состоит из ступенчатых колес 1—3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на колесо 1. Радиусы ступеней колес равны соответственно: у колеса 1 — r₁ = 2 см, R₁ = 4 см, у колеса 2 — r₂ = 6 см, R₂ = 8 см, у колеса 3 — г₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки А, В и С.

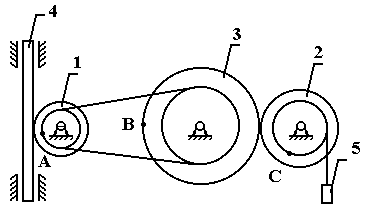
₁ = 2t² — 9 — закон вращательного движения колеса 1.

Определить в момент времени t₁ = 2 с скорость v₄; ₂; ускорения ₂; a_С; а₅.

Решение. Будем обозначать скорости точек, лежащих на внешних ободах колес (радиуса R_i), через v, а точек, лежащих на внутренних ободах (радиуса r_i), — через u.

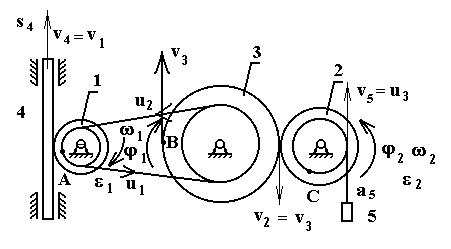
1. Зная закон вращательного движения колеса 1, определяем угловые скорости всех колес как функции времени t:

.

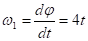
Так как рейка 4 находится в зацеплении с колесом 1, то v₄ = v₁=₁R₁=16t. При t = 2 с, v₄ = 32 м/с Так как колёса 3 и 1 находятся соединены через передачу, то u₃=u₁, то есть скорость равновесный пространственный.

=8t.

Тогда, угловая скорость колеса 3 будет определяться по формуле:

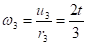
Так как колесо 3 и колесо 2 находятся в зацеплении, то v₃ = v₂ или.

v₂=v₃=₃R₃=t32/3.

Угловая скорость колеса 2:

.

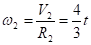
При t = 2 с ₂ = 2,67 с^-1.

Груз 5 находится в зацеплении с внутренним ободом колеса 2. Поэтому, v₅ =u₂.

Определяем u2.

.

2. Определим угловые ускорения всех колес.

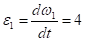
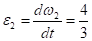
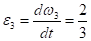
с^-2; с^-2; с^-2.

4. Определим неизвестные ускорения.

Ускорение груза 5 по формуле:

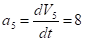
см/с²

Ускорение тоски С найдём по формуле:

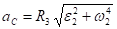
=7,25 см/с²

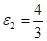
Ответ: v₄ = 32 см/с,: ₂ = 2,67 1/с, с^-2, а₅ = 8 см/с²; а_С = 7,25 см/с²

Задача К3.

Круглая пластина радиуса R = 60 см вращается вокруг неподвижной оси по закону = 6t³-12t². Положительное направление отсчета угла показано на рисунке дуговой стрелкой.

По пластине по окружности радиуса R из точки, А движется точка М; закон ее относительного движения, т. е. зависимость.

s=AM= R (2t² — 1)/3.

расстояние l = R. На рисунке точка М показана в положении при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А).

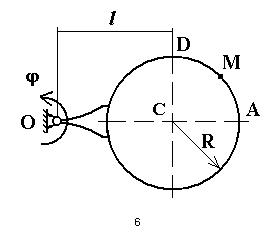
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t₁ = 1c.

Решение. Рассмотрим движение точки М как сложное, считая ее движение по прямой AB относительным, а вращение плиты — переносным движением. Тогда абсолютные скорость и ускорение найдутся по формулам:

V_aб = V_от + V_nep, а_аб = a_от + a_пер +a_кор

Определим все характеристики относительного и переносного движений.

Относительное движение происходит по закону.

s=AM= R (2t² — 1)/3.

Установим, где будет точка М в момент времени t₁. Полагая t₁=1c, получим s₁ = R/3. Покажем на рисунке точку в положении, определяемым этим расстоянием (Точка M). Получим, что МСА = 60.

Теперь находим численные значения скорости и ускорения:

V_от = s' =R4t/3; а_от= V_OT'=4R/3, а_nот = V_ot²/R.

Для момента времени t₁ = 1c получим:

V_ot = 251.2 cм/с; а_от= - 251.2 cм/с², а_nот =10 052 cм/с²

Покажем все эти векторы на рисунке.

ПЕРЕНОСНОЕ ДВИЖЕНИЕ происходит по закону = 6t³-12t² Найдем угловую скорость и угловое ускорение .

= ' = 18t -24t², = '=18 — 48t.

При t₁ = 2c получим ₁ = -6 с^-1, = -40 с^-2.

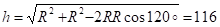
Для определения V_nep и а_пер найдем расстояние h точки M от оси вращения по теореме косинусов. Получим см. Тогда, в момент времени t₁ = 2c.

V_nep = ₁ h =-696 см/с, a_nep= V_nep = 4640 см/с², a_nпep= ₁² h = 4176 см/с².

Изображаем на рисунке полученные векторы.

Кориолисово ускорение находим как векторное произведение угловой скорости и относительной скоростью V_отн.

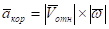
Так как угол между вектором и относительной скоростью Vотн составляет 90°, то в момент времени t1 = 2c.

а_кор =2|||v_OT| sin90° = 3014,4 см/с².

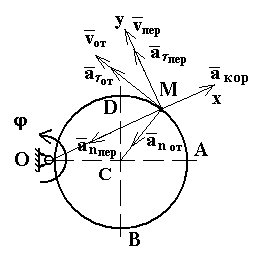
Направление вектора а_кор найдем, спроектировав вектор v_ot на плоскость, перпендикулярную оси вращения, и повернув эту проекцию в сторону на 90°.

Определяем v_aб по теореме косинусов:

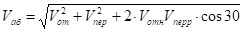
V_аб = 494,7 см/с.

Определяем а_аб по теореме о сложении ускорений:

а_аб = a_от + a_пер +a_кор + a_nпер

Для определения ааб проведем координатные оси xy и вычислим проекции вектора ааб на эти оси. Тогда, для момента времени t1 = 2c получим:

а_абх = а_кор — а_nпер — а_nот cos30 — а_от cos60 = - 9741см/с²;

а_абу =a_пер + а_отcos30 — а_nпер sin30 = -603.5 cм/с².

Отсюда находим а_аб

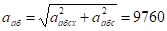
cм/с²

Ответ: v_a6 = 494.7 см/с, а_аб = 9760 см/с²