Свертка сигналов. 
Свертка сигналов и спектральный анализ

Линейная и циклическая свертки

Дискретным эквивалентом линейного аналогового фильтра (согласованного, полосового и т. п.), выходной сигнал которого определяется интегралом свертки.

является дискретный фильтр, формирующий весовую сумму (линейную свертку):

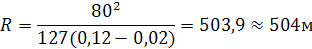
(k-n)0. (99).

Здесь x[n]=x(nt), n=0,1,2,…, — сигнал на входе фильтра, h[k-n] - весовые коэффициенты, определяющие импульсную характеристику аналогового фильтра h(t), N— объем выборки. Для реализации цифрового фильтра необходимы устройства, выполняющие операции сложения, умножения и задержку.

В более общем виде можно рассмотреть класс линейных инвариантных к сдвигу (ЛИС) систем, который включает много полезных, широко используемых методов обработки сигналов, в том числе и фильтрацию сигналов. Соотношение вход-выход для ЛИС систем задается в виде свертки.

.

где — входной сигнал; - множество отсчетов выходного сигнала; - импульсный отклик ЛИС системы; символ звездочка как двучленный оператор означает свертку.

Система ЛИС полностью определяется своим импульсным откликом. Считается, что система является каузальной тогда и только тогда, когда при n < 0.

Если импульсная реакция имеет конечную длительность, то бесконечная сумма сводится к конечной сумме.

.

Предположим, что обрабатываются два каузальных цифровых сигнала длиной L и длиной M. Тогда линейная (апериодическая) свертка этих сигналов имеет длину (L + M -1) и определяется как.

. (100).

Если L = M, то выражение для линейной свертки можно записать в матричном виде.

. (101).

В большинстве алгоритмов вычисления свертки входная последовательность делится на последовательные блоки по L отсчетов и вычисляется как сумма линейных сверток каждого из этих блоков с M точечной последовательностью .

Используя понятия алгебры полиномов, процесс вычисления линейных сверток y () можно представить в виде произведения двух полиномов x () и h ():

,.

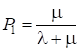
. (102).

Рассмотрим поведение свертки относительно дискретных преобразований. Начнем с дискретного преобразования Лапласа. Z-преобразование дискретной последовательности имеет вид.

.

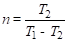
Фундаментальным свойством ЛИС является соотношение, согласно которому операция свертки во временной области, соответствует операции умножения в области Z-преобразований:

. (103).

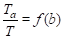
Важным классом ЛИС систем являются системы, имеющие z — преобразование в виде рациональных функций. В этом случае H (z) = B (z)/A (z), где и — полиномы конечной степени. Так как Y (z) = H (z) X (z), то получаем A (z) Y (z) = B (z) X (z). Во временной области отклик системы и входное воздействие связаны между собой разностным уравнением.

.

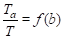
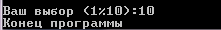
Без потери общности можно положить a₀ = 1. Тогда отклик системы на заданное входное воздействие при известных начальных условиях запишется как следующее рекуррентное соотношение.

.

Заметим, что в рекуррентном соотношении каждая сумма представляет собой оператор свертки. Импульсный отклик такой системы имеет бесконечную длительность. Такие системы называют системами с бесконечной импульсной характеристикой (БИХ) или рекурсивными системами.

Важный подкласс множества рациональных Z-преобразований имеет знаменатель A (z) =1. В этом случае рекуррентное соотношение не содержит членов обратной связи, а отклик y[n] представляет собой просто свертку входного воздействия x[n] с коэффициентами b_k полинома B(z). Такие системы часто называют системами с конечной импульсной характеристикой (КИХ) или нерекурсивными системами.

Определим ДПФ для входного воздействия и импульсной характеристики ЛИС:

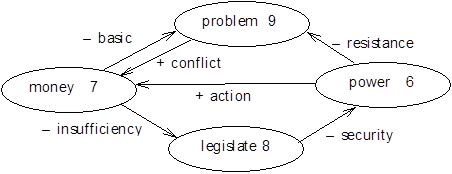
и .

Рассмотрим обратное ДПФ произведения двух ДПФ X(k) H(k):

.

Подставив сюда определение X(k) и изменив порядок суммирования, получаем.

.

откуда следует.

.

Для того чтобы полученное выражение имело смысл, необходимо периодически продолжить сигнал h[n-l] с периодом N. С учетом периодического продолжения выражение для y[n] можно переписать как.

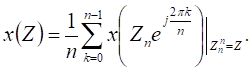
. (104).

В силу периодичности последовательностей номера отсчетов берутся по модулю N, поэтому x[-n] = x[N-n] и h[-n] = h[N-n]. Полученная сумма называется N-точечной циклической сверткой. В матричном виде циклическая свертка записывается как.

(105).

Матрица вида относится к классу ганкелевых, а матрицу вида часто называют циркулянтной, или теплицевой. Циркулянтные матрицы занимают особое место в области математики, связанной с разработкой эффективных алгоритмов [5].

Используя алгебру полиномов, циклическую свертку можно записать в виде произведения двух многочленов свертываемых последовательностей по модулю полинома (^N-1):

. (106).

В матричном виде, через матрицы Ганкеля и Теплица циклическая свертка запишется как.

Если обозначить значения линейной и циклической сверток соответственно как и, при L=M=N можно выразить одни значения свертки через другие следующим образом:

Таким образом, если положить равными нулю значения, ,, то линейную свертку можно вычислить через циклическую.

Полином линейной свертки имеет степень L+M-2 и он совпадает со своим вычетом по модулю полинома p(), имеющего степень L+M-1:

.

Предположим, что полином модуля разлагается на взаимно простые линейные множители над полем коэффициентов F.

.

где a_i-есть L+M-1 различных корней p() в поле F.

Согласно алгоритму Тоома-Кука линейная свертка может быть вычислена за L+M-1 операций умножения. При этом x[i], h[i] - рассматриваются как переменные, через которые выражаются значения y[i]. Для этого следует выбрать L+M-1 различных чисел (интерполяционных узлов) _i и подставить их вместо в выражение для свертки. Получим произведения линейных выражений. Затем применим интерполяционную формулу Лагранжа для однозначного определения полинома степени L+M-2:

. (107).

С другой стороны, полиномы x(_i=a_i), h(_i=a_i) можно рассматривать как вычеты полиномов h_i() x_i() по модулю (-a_i):

.

Полином свертки может быть восстановлен по формуле.

.

где, ,.

. (108).

Так как поле коэффициентов F и интерполяционные узлы могут быть выбраны произвольно, то в качестве a_i — выберем набор из L+M-1 последовательных степеней числа W, считая их попарно различными в поле F. В этом случае и приведение по модулю (- a_i) выражается следующим образом:

.

Аналогичное выражение получается и для. Таким образом, в результате специального набора a_i алгоритм Тоома-Кука сводится к вычислению циклических сверток с помощью преобразований, имеющих структуру ДПФ.

Если, то алгоритм Тоома-Кука можно рассматривать как вычисление апериодической свертки с помощью ДПФ. В этом случае полином p() имеет вид.

.

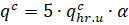
Следовательно, если узлы интерполяции выбираются комплексными корнями из единицы, то алгоритм Тоома-Кука эквивалентен вычислению с помощью ДПФ циклической свертки двух входных последовательностей длиной L+M-1, получающихся добавлением (L — 1) нулей к h и (M — 1) нулей к x.