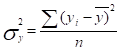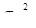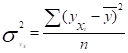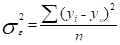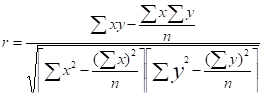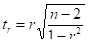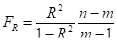Анализ связи парной корреляции. 
Оценка практической значимости синтезированной модели

4.Оценка практической значимости синтезированных моделей.

Мы должны обосновать применение метода функционального анализа при изучении корреляционной зависимости. Для этого докажем, что применение метода функционального анализа при изучении корреляционной зависимости не дает существенных погрешностей.

Это осуществляется посредством показателей тесноты связи между признаками х и у.

Для статистической оценки тесноты связи между признаками х и у применяются следующие показатели вариации:

1) Общая дисперсия результативного признака, отображающая совокупное влияние всех факторов.

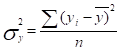
(15).

Где у_i — эмпирические значения.

— общая средняя теоретических (выровненных) значений.

Отклонения обусловлены тем, что сочетание факторов, влияющих на вариацию признака у, для каждой единицы анализируемой совокупности различно.

2) Факторная дисперсия результативного признака отображающая вариацию результата у только от воздействия изучаемого фактора х

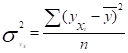
(16).

где — теоретические (выровненные) значения.

Факторная дисперсия характеризует отклонения выровненных значений от их общей средней величины.

3) Остаточная дисперсия отображает вариацию результативного признака у от всех прочих, кроме х, факторов.

. (17).

Остаточная дисперсия характеризует отклонения эмпирических (фактических) значений результативного признака у от их выровненных значений .

5. Индекс детерминации (причинности) R² выражает долю факторной дисперсии в общей дисперси. При прямолинейной форме связи определяется линейный коэффициент корреляции r :

.(22).

6. Показатели тесноты связи для небольших статистических совокупностей могут искажаться действием случайных причин, поэтому возникает необходимость проверки их существенности. Для оценки значимости r (линейного коэффициента корреляции), применяется t — критерий Стьюдента. Определяется фактическое значение критерия:

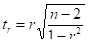
(23).

Далее рассчитанное значение критерия t_r сравнивается с критическим t_k, взятым из таблицы Стьюдента с учетом б (уровня значимости) и k (числа степеней свободы).

Если t_r > t_k, то величина линейного коэффициента корреляции r — существенна.

Для оценки значимости R (эмпирического корреляционного отношения), применяется F — критерий Фишера.

Определяется фактическое значение критерия:

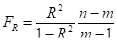
(24).

Здесь m — число параметров уравнения регрессии.

Далее рассчитанное значение критерия F_R сравнивается с критическим F_k из таблицы F — критерия с учетом б (уровня значимости) и k₁ = m-1; k₂ = n-m (числа степеней свободы) Если F_R > F_k, то величина эмпирического корреляционного отношения R — существенна.