Распространение волн в неоднородных средах

Рассмотрим простейший случай — плоскую гармоническую волну, распространяющуюся в неоднородной линейной изотропной среде. Тогда уравнение Гельмгольца (1.10) принимает вид.

u + k2®u = 0. (7.1).

Общего решения при произвольной зависимости k® это уравнение не имеет, поэтому интерес представляют приближенные решения, одним из которых является приближение геометрической оптики, справедливое при достаточно медленной зависимости параметров среды от координат.

Приближение геометрической оптики Будем искать решение уравнения (7.1) в виде волны ММАФ:

u® = A®exp (ik0®), (7.2).

где ® — эйконал, k0 = /c — волновое число в вакууме. Подставляя соотношение (7.2) в уравнение (7.1), получим:

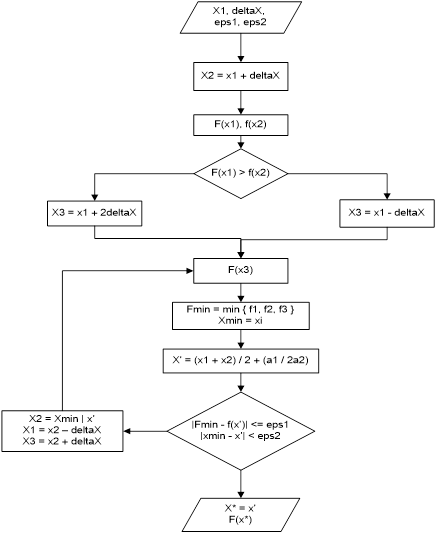
. (7.3).

Если |grad A| << k0A, |grad | << k0, |grad k| <> = 2/k0, и на расстоянии << l << L волну можно считать плоской, а ее направление в изотропной среде охарактеризовать нормалью к поверхности волнового фронта ® = const. В этом случае можно считать, что первое слагаемое, имеющее порядок малости 2/(42L2), существенно меньше второго и третьего слагаемых, имеющих порядок малости /(2L), и четвертого слагаемого, не зависящего от отношения /(2L). Пренебрегая в уравнении (7.3) первым слагаемым и выделяя мнимую и действительные части, получим:

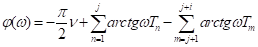
— (7.4).

уравнение эйконала,.

A + 2 (grad) (grad A) = 0 — (7.5).

уравнение переноса.

Отметим, что для электромагнитных волн в линейной среде уравнение эйконала может быть получено из уравнений Максвелла (2.15) для комплексных амплитуд.

.

Будем искать их решение в виде волны ММАФ (7.2):

E = E0®exp (ik0), |rot E0| << k0|E0|, H = H0®exp (ik0), |rot H0| << k0|H0|.

Тогда уравнение нулевого приближения принимает вид.

[(grad) E0] = -H0, [(grad) H0] = E0. (7.6).

Исключим из уравнений (7.6) вектор H0:

[(grad) [(grad) E0]] + E0 = 0,.

(grad) ((grad) E0) — E0 (grad)2 + E0 = 0.

Из уравнений (7.6) следует, что векторы E0, H0 и grad взаимно перпендикулярны, то есть (grad) E0 = (grad) H0 = E0 H0 = 0. Тогда (grad)2 = = n2, что совпадает с уравнением (7.4).

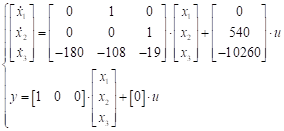
Введем единичный вектор l = (grad)/|grad |, подставив его в уравнение (7.6) и учитывая, что, получим уравнение плоских волн.

.

совпадающее с уравнением (1.26), если заменить вектор m на вектор l. Поскольку волновой фронт определяется уравнением ® = const, то вектор l является нормалью к волновому фронту.

С другой стороны, подставляя поле H0 из первого уравнения (7.6) в выражение (1.35) для усредненного вектора Пойтинга в гармонической электромагнитной волне и учитывая условие (grad) E0 = 0, получим:

.

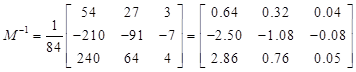
то есть вектор l параллелен усредненному вектору Пойтинга и определяет направление переноса энергии.

Будем называть геометрическим световым лучом направленные линии, касательные к которым в каждой точке пространства совпадают с направлением переноса энергии, то есть с вектором l. Из определения следует, что луч всегда перпендикулярен поверхности волнового фронта. Если параметрическое уравнение луча имеет вид r = r (s), где s — длина дуги, то нетрудно показать, что.

dr/ds = l = (grad)/n, (7.7).

d (nl)/ds = grad n, (7.8).

d/ds = n. (7.9).

Действительно, с учетом уравнений (7.4) и (7.7) получаем.

d/ds = dr/ds (grad) = l (nl) = n, d (nl)/ds = d (grad)/ds = grad (d/ds) = grad n.

Если траектория луча определена, то из уравнения (7.9) можно найти эйконал:

. (7.10).

Часто вводят лучевые координаты, связанные с лучами. Пусть волновой фронт определен уравнением ® = 0, и криволинейные координаты и определяют положение точки М0 на поверхности ® = 0. Из каждой точки.

М0(,) проведем луч, перпендикулярный волновому фронту в этой точке, тогда все точки на луче можно охарактеризовать величиной эйконала вида (7.10):

волна гармонический плоский.

.

Тогда уравнение r = r (, ,) при постоянных и описывает луч, а при постоянной — волновой фронт.

Умножим теперь уравнение переноса (7.5) на, А и получим.

div (A2 nl) = 0. (7.11).

Рассмотрим на поверхности волнового фронта = 1 малую площадь d1, ограниченную некоторым потоком лучей, на которой, А = А1. Проведем эти лучи до пересечения с другим волновым фронтом = 2, на котором они ограничат площадь d2. Проинтегрируем по объему внутри полученной лучевой трубки соотношение (7.11):

.

В силу произвольности выбранных волновых фронтов nA2d = const. Тогда для интенсивности в произвольном сечении получаем.

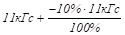
. (7.12).

Решить уравнения (7.8) и (7.12) можно лишь в частных случаях. Если.

n = const, то r = as + b, то есть в однородной среде лучи прямые. Отметим, что при схождении лучевого потока в точку (фокус) интенсивность там обращается в бесконечность и меняется очень быстро, то есть вблизи таких точек (каустика) приближение геометрической оптики неприменимо.

Геометрическая оптика слоисто-неоднородной среды Рассмотрим сферически-слоистую среду, в которой показатель преломления зависит только от расстояния r до некоторого центра. Тогда с учетом уравнений (7.7) и (7.8) получим:

.

то есть n[r l] = const. Таким образом, в сферически неоднородной среде лучи являются плоскими кривыми, лежащими в плоскости, проходящей через начало координат, и вдоль каждого луча.

nrsin () = const, (7.13).

где — угол между касательной l к лучу и радиус-вектором r.

Соотношение (7.13) является законом Снелиуса для сферически-слоистой среды. Если задано, что n (r0) = n0 = 1, (r0) = 0, то.

nrsin () = r0sin (0). (7.14).

Если задать траекторию луча уравнением r (), где — полярный угол, то с учетом соотношения (7.14) получаем.

. (7.15).

Для плоскослоистой среды с законом преломления n (z), в которой луч распространяется в плоскости xz, уравнение (7.8) принимает вид:

d (nsin ())/ds = n/x = 0,.

где — угол между вектором l и осью z, или.

n (z)sin ((z)) = const = sin (0). (7.16).

Соответствующее уравнение траектории z (x) имеет вид:

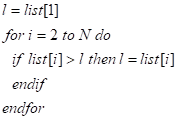
. (7.17).

Из уравнения (7.17) видно, что по мере распространения в среде угол наклона луча к вертикали изменяется, то есть лучи искривляются. Это явление называется рефракцией.

Отметим, что если r0 — радиус Земли, а z — высота над уровнем моря, то.

r = r0 + z, (0) = 0, и уравнение (7.14) принимает вид.

n (z)(1 + z/r0)sin () = sin (0), (7.18).

аналогичный уравнению (7.16), если ввести приведенный коэффициент преломления nпр (z) = n (z)(1 + z/r0), что позволяет свести задачу о распространении радиоволн вокруг Земли к более простой задаче о рефракции в плоскослоистой среде. При z << r0 можно положить расстояние вдоль поверхности Земли равным x = r0, тогда с точностью до слагаемых порядка z/r0 получаем:

.

Траектории луча при различных законах изменения показателя преломления n (z) рассматриваются в курсе оптики. Для определения же поля в приближении геометрической оптики необходимо знать амплитуду и фазу волны в каждой точке, через которую проходит луч, то есть найти функции A® и ®. Для плоскослоистой (x, z) среды уравнение эйконала (7.4) принимает вид:

(/x)2 + (/z)2 = n2(z). (7.19).

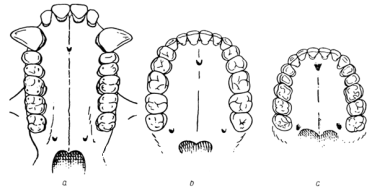
Из уравнения (7.8) следует, что если коэффициент преломления среды является функцией координаты z, то, то есть,.

/x = const. Если при z = 0 направление луча составляет угол 0 с осью z, а.

n (0) = n0 = 1, то с учетом уравнения (7.7) получаем /x = sin (0). Тогда из уравнения (7.19) получим: (/z)2 = n2(z) — sin2(0), то есть.

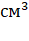
. (7.20).

Знак перед корнем определяется направлением распространения луча.

Изменение амплитуды вдоль луча можно найти из уравнения переноса (7.5) с учетом уравнения (7.20). Учитывая, что в силу уравнения (7.16).

.

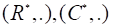
получаем.

2[sin (0) A/x + ncos () A/z] = -Ad[ncos ()]/dz. (7.21).

Решением уравнения (7.21) является функция.

.

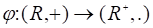
Тогда с учетом уравнений (7.2) и (7.20) поле волны в слоистонеоднородной среде в приближении геометрической оптики можно записать в виде двух волн, бегущих «вверх» и «вниз» :

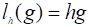
(7.22).

Обе волны, описываемые формулой (7.22), распространяются независимо, отражения от неоднородной среды в приближении геометрической оптики не происходит. Отметим, что амплитуду каждой из двух волн вида (7.22) можно записать в виде.

u (x, z) = exp (ik0xsin (0))f (z), (7.23).

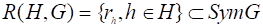
где функция является приближенным решением Вентцеля, Крамерса, Бриллюэна (ВКБ) уравнения.

d2f/dz2 + k02[n2 — sin2(0)]f = 0, (7.24).

которое получается подстановкой выражения (7.23) в уравнение Гельмгольца (7.1). Точное решение этого уравнения возможно только при некоторых законах изменения n (z).