Анализ статистических нелинейностей в сахарной подотрасли АПК

АНАЛИЗ СТАТИСТИЧЕСКИХ НЕЛИНЕЙНОСТЕЙ В САХАРНОЙ ПОДОТРАСЛИ АПК

Мир линейных функций утомительно однообразен: стоит изучить лишь одну линейную функцию, и вы знаете все существенное о линейных функциях. А мир нелинейных функций так же, как и стоящий, за ним мир нелинейных явлений, страшит, покоряет и манит своим неисчерпаемым разнообразием.

На одинаковые приращения независимой переменной одна и та же нелинейная функция откликается по-разному в зависимости от того, какому значению независимой переменной придается приращение. Почти полным безразличием к изменению одних и повышенной чувствительностью к изменению других значений независимой переменной нелинейные функции разительно контрастируют с линейными. Именно здесь и проходит демаркационная линия между миром нелинейных и миром линейных явлений.

Границу между линейными и нелинейными теориями принято проводить по иному признаку. Теория считается линейной или нелинейной в зависимости от того, какой — линейный или нелинейный — математический аппарат она использует.

Современные математические модели представляют собой нелинейные уравнения или системы нелинейных уравнений различных типов. Хотя нелинейные уравнения несколько утратили былой ореол неприступности, все же найти аналитически замкнутое решение удается лишь в исключительных случаях. Точно решаемые модели обычно не находят, а специально конструируют, чтобы отработать на них стратегию и тактику штурма не решаемых точно моделей. Обычно успеха удастся добиться, комбинируя численные и аналитические методы. Н. Забуский назвал комбинированный подход синергетическим (от греческого «синергетика» — совместное, или согласованное действие). «Синергетический подход к нелинейным математическим и физическим задачам, — писал он, — можно определить как совместное использование анализа и численной машинной математики для получения решений разумно поставленных вопросов относительно математического и физического содержания уравнений».

Неоспоримое превосходство нелинейности даёт возможность исследовать работу в любой области с более реальным подходом к действительности, в частности, в области эластичности спроса и предложения на продукцию предприятия.

В соответствии с законом спроса существует обратная зависимость между ценой товара и объемом спроса, выражаемая графически в виде кривой спроса (рис.1), имеющей отрицательный наклон.

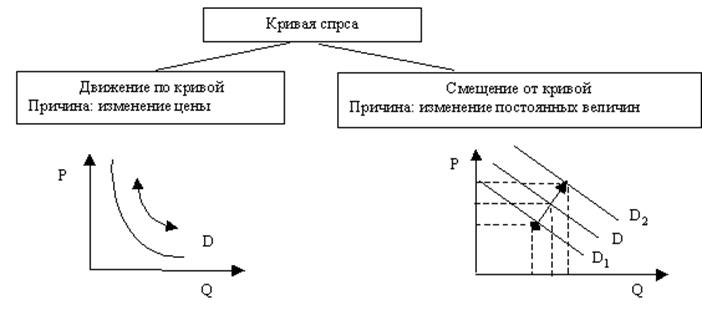
Рис. 1 Представление спроса

Зависимость объема спроса от определяющих его факторов называют функцией спроса:

где Q — объем спроса на сахар; P — цены на сахар; D — спрос (от англ. demand — спрос); S — предложение (от англ. supply — предложение).

Закон предложения утверждает, что, при прочих равных условиях, объем предложения увеличивается месте с ценой товара. Эта прямая зависимость графически выражается восходящей кривой предложения (см. рис.2).

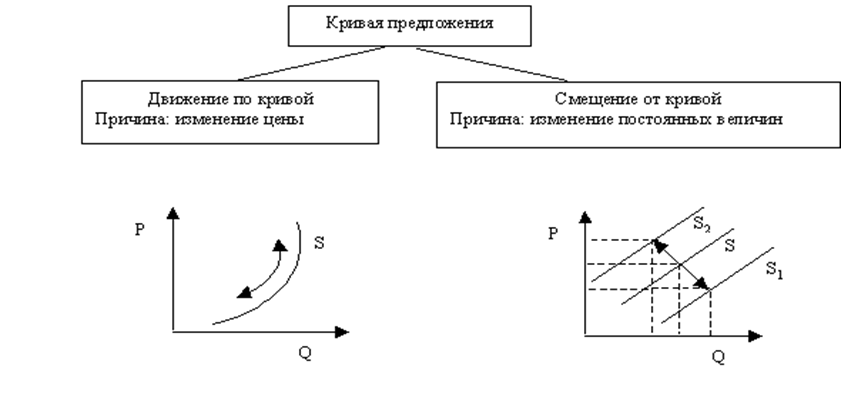
Рис. 2 Представление предложения

Известно, что, зная кривую спроса, можно построить кривая предложения, и наоборот. Поэтому, рассмотрим функцию ценовой эластичности спроса (E_d), как базовую при построении квазиоптимальной области. E_d измеряют чувствительность потребительского спроса к изменению цены продукции. Значение E_d определяется, как отношение процентного измерения объёма сбыта продукции к процентному изменению цены продукции:

где — изменение первоначального объёма сбыта () при изменении начальной цены () на величину, %.

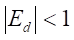
В экономической теории принято различать эластичный спрос и неэластичный спрос. Строго говоря, спрос считается эластичным, если значение ценовой эластичности спроса по модулю больше единицы:. Если, то спрос неэластичный [1]. В зоне эластичного спроса при снижении цены доход предприятия увеличивается, в зоне неэластичного — уменьшается.

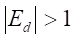
Используя формулу (1) находим спрос на сахар в 2005 год для N-го сахарного завода, производительная мощность которого составляет 3200 тонн/сут. Посуточная реализация сахарного песка отражает его отгрузку со склада завода. Индексы цен на сахар взяты по данным Института конъюнктуры аграрного рынка (ИКАР). На рис. 3 представлена полученная диаграмма чувствительности спроса на сахар.

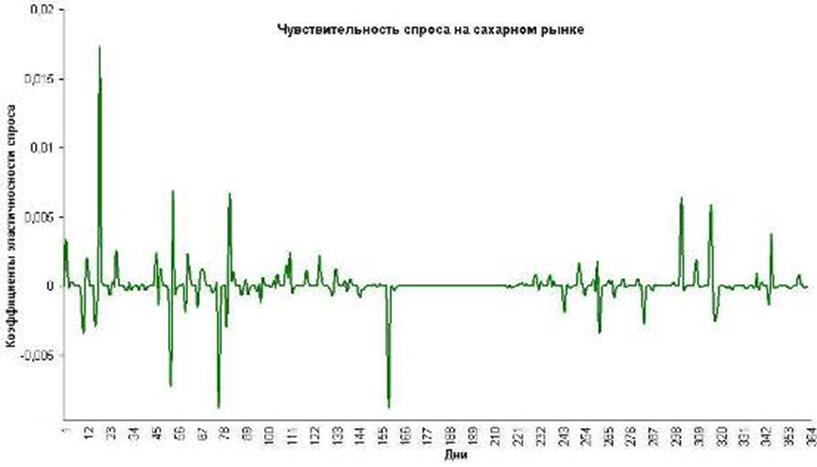
Рис. 3 График чувствительности спроса на рынке сахара

Величина спроса как скалярная (абсолютная) всегда положительна, поэтому необходимо все её отрицательные значения перевести в положительную область путём умножения на -1. На рис. 4 представлены результаты этой операции. Резкие колебания спроса объясняется тем, что из 365 дней в году 104 дня выходных, 12−13 дней праздничные дни и плюс к тому же дней 40 завод простаивает из-за перехода с одного продукта переработки на другой. Получается, сахарный завод работает 208−209 дней в году или 57% от всего года.

При нахождении процентных отношений приращений сбыта () или цены () по формуле (1) необходимо учитывать погрешность при вычислении кривой спроса, обусловленную переходом от дискретного представления данных к аппроксимации с помощью непрерывной кривой. Эта погрешность чем меньше, чем лучше аппроксимирующая кривая соответствует исходным дискретным данным.

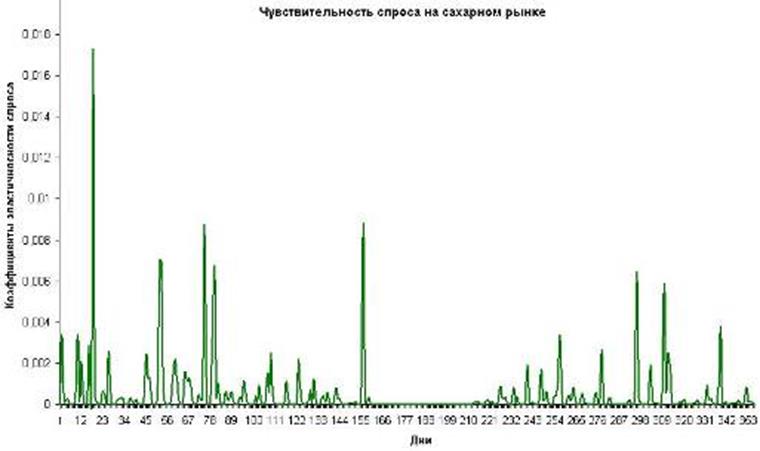
Рис. 4 Скалярное представление кривой спроса

Построения графика спроса осуществлялось следующим путём. На кривой спроса были выбраны 9 характерных точек, по которым строилась функция спроса.

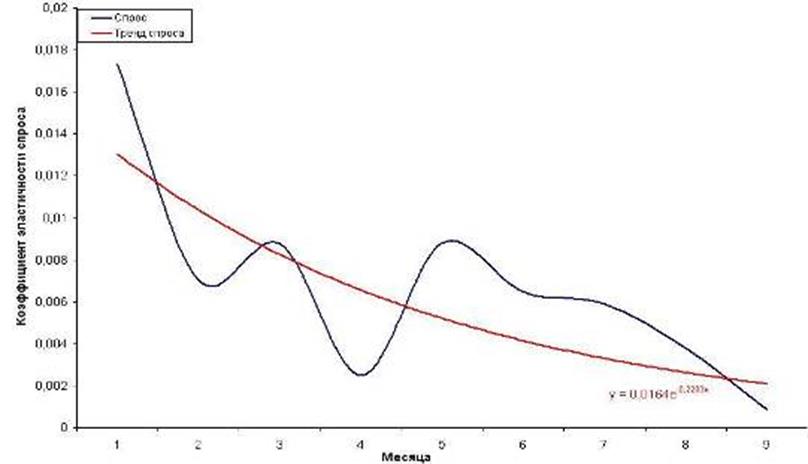
Рис. 5 График спроса и его тренд с уравнением

Лучшей аппроксимирующей функцией оказалась функция (2), которая и представлена на рис. 5.

у_сп =0, 0164e^{-0, 2293} (2).

Зная эту функцию спроса, построим соответствующую ей кривую предложения (см. рис. 6 формулу (3)).

y_пр =0, 0017e^{0, 2293} (3).

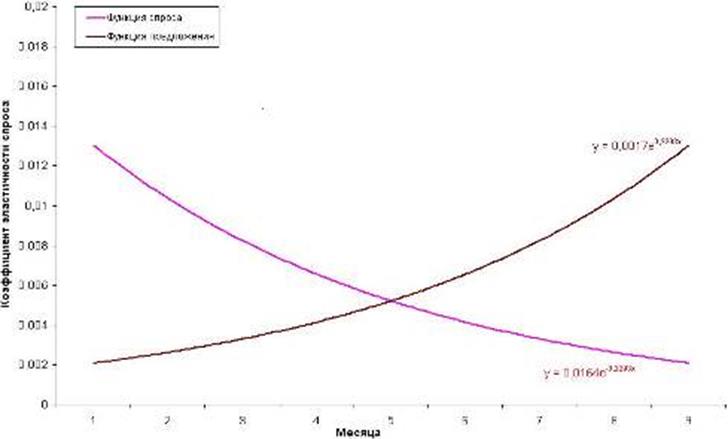
Рис. 6 Результат вычисления функций спроса и предложения

Далее были найдены коэффициенты, обеспечивающие перевод представленных данных к универсальному (безразмерному) виду. После нахождения коэффициентов функции спроса (2) и предложения (3) преобразовались к виду (4) и (5):

y_сп =2 080 0000e^-0,0066 (4).

y_пр =220 0000e^{0, 0066} (5).

Этих унифицированных функций представление рис. 7.

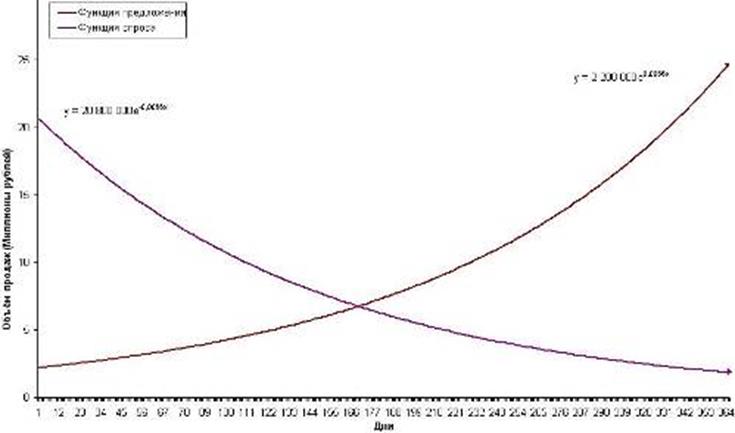
Рис. 7 Пропорциональное представление функций спроса и предложения

На рис. 7 необходимо нанести кривую продаж, чтобы определить квазиоптимальную область деятельности сахарной подотрасли. Для этого по данным продаж сахарного песка N-го сахарного завода в 2005 году осуществим аппроксимацию с помощью пяти функций: линейной, логарифмической, экспоненциальной, степенной и полиноминальной. Лучшей аппроксимирующей функцией (рис.8) оказалась полиноминальная функция (6).

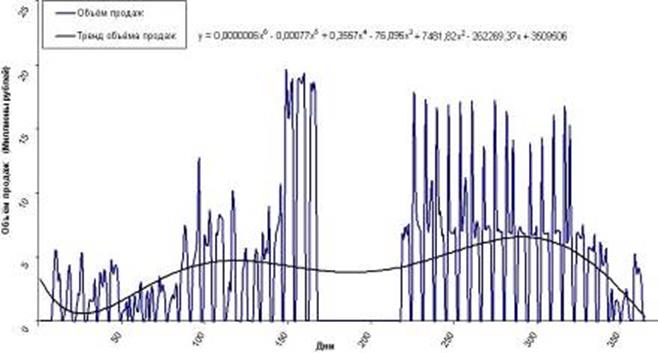
Рис. 8 Объём продаж сахара и тренд объёма продаж N-го сахарного завода

y₂ = 6Ч10^-7x⁶ — 0,00077x⁵ + 0,3557x⁴ — 76,095x³ +7481,82x² ;

-262 269,37x + 3 509 506 (6).

Результат суперпозиции унифицированных кривых спроса предложения и продаж представлены на рис. 9. При этом образуется шесть пересечений и соответственно четыре фигуры (области). Из них три пересечения формируют квазиоптимальную область (S_АВС) объёма продаж сахара. Область (S_DE), показывает пребывание субъектов рыночных отношений в пассивности. Точки E и A образуются при пересечении функций тренда продаж и предложения. Область (S_EА), показывает активность покупателей, то есть, спрос на сахар. А вот область (S_CF) демонстрирует обратный процесс, превалирование предложение над спросом.

Календарно эти области можно представить, как: область S_DE охватывающая период с 8ч9 января по 15ч16 марта, область S_EА — с 15ч16марта по 15ч16 мая, область S_АВС — с 15ч16 мая по 17ч18 августа и область S_CF — с 17ч18 августа по 20ч21 декабря. По сути, на рис. 9 образована, своего рода, кривая, описанная тремя точками: D, B и F.

Для более объективного представления рассчитаем их площади. Так: S_DE = 34 173 063, S_EА = 1 996 798 052 и S_CF = 3 596 101 454. Площадь S_АВС представляет собой наибольший интерес и будет рассмотрена дальше.

Сущность работы заключается в нахождении область квазиоптимальности. Эта область образуется при пересечении трех кривых: спроса, предложения и тренда продаж за 2005 год.

Для более насыщенного представления она заштриховывается поперек в отличие от других областей и обозначается через точки пересечения, показанные на диаграмме (см. рис.9), буквами: А, В и С.

График, изображённый на рис. 9 показывает комплексные параметры, задействованные в определении квазиоптимальных значений сахарного завода и других смежных областей.

Прежде чем описать область, для четкого уяснения поясним, что такое тенденция. Это кривая, которая показывает динамику, очищенную от случайных влияний и индивидуальных особенностей отдельных периодов, или тенденция — это общее направление изменения цен на рынке. Для детального представления графического коллажа начнем с точек.

Точка А представляет собой пересечение полиноминальной кривой продаж y₂ с экспоненциальной кривой спроса y (у_сп), образуя первую точку квазиоптимальной области с координатами (135; 6 697 576). Именно эта точка является входным показателем, то есть спрос, и тенденция реализации сахара на рынке находят первый справедливый баланс в году. Иначе говоря, точка этого баланса приходится на 15 — 16 мая 2005 года, когда потребители сахара начинают предлагать реальную цену на продукт. Постепенно готовясь к тому, что сахарные заводы прекращают выработку сахара из сахарного сырца и дело идёт к остановке производства для перехода на сахарную свеклу. На рынке создаётся ажиотаж покупателями сахарной продукции, для этого они делают запасы.

Другая точка С представляет собой пересечение y₂ с кривой предложения y₁ (у_пр ) в последней точки квазиоптимальной области с координатами (228; 6 492 357). Условно говоря, данная точка определяется, как справедливая последняя цена на сахар, то есть идет превалирование предложение над спросом. Эта точка характеризуется на оси Х, как 17 — 18 августа 2005 года. Когда спрос на сахарную продукцию начинает падать, выходя из квазиоптимальной области, и цена достигает предельно допустимое значение в целом по всему рисунку.

Что касается точки В, то она возникает при пересечении двух кривых: спроса и предложения. Позиционируя себя в точке (179; 7 855 516) или 28 — 29 июня 2005 года. Пресечение кривых спроса и предложения определяют цену равновесия (или рыночную цену) и равновесное количество продукции. Этот момент является пиковым или балансовым, в связи с тем, что достигается апогей для спроса и предложения когда, как правило, сезон переработки сахарного сырца закончен, а сезон выработки сахара из сахарной свеклы ещё не начат.

Квазиоптимальная область, как видно из рис. 9, образуется при пересечении этих точек: А, В и С. Именно эта область (S_АВС) в виде «лезвия секиры».

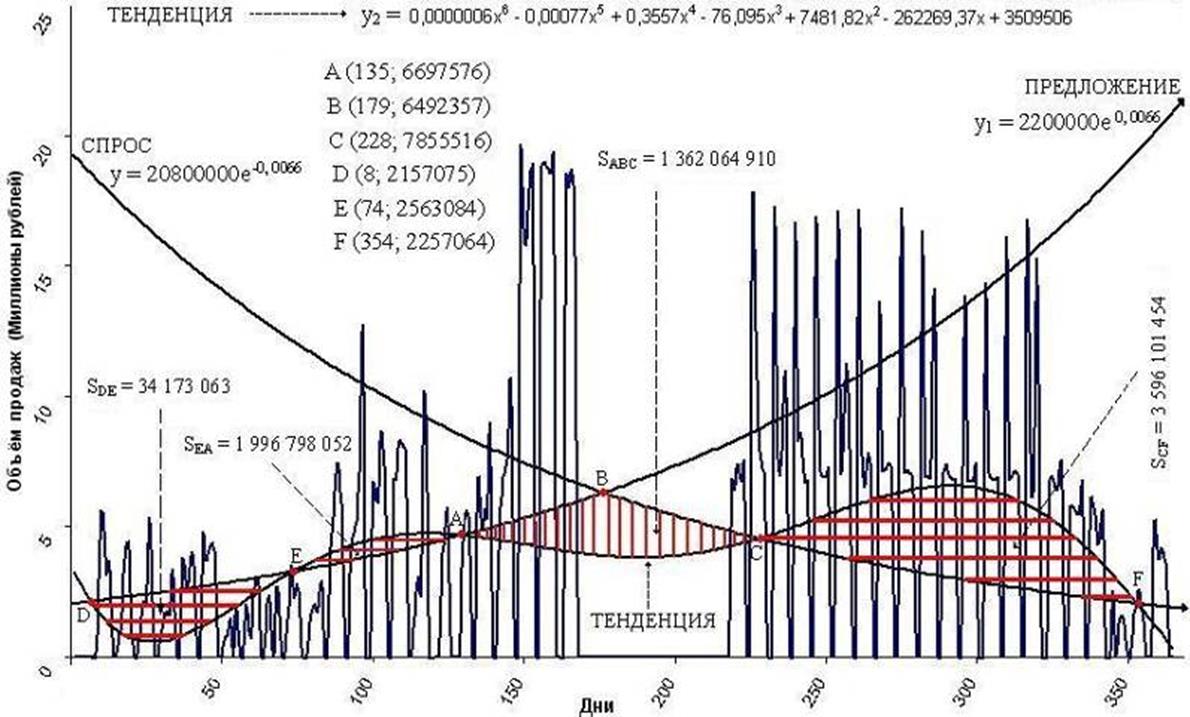
Рис. 9 График квазиоптимальной области объёма продаж сахара и другие смежные области

представляется как излишек спроса (см. рис. 10) на сахар, то есть можно предположить благоприятное развитие событий не только для сахарного завода, но и для свеклопроизводителя, который тоже получает прибыль от реализации сахара. Если представить, что сахарный завод и агрохозяйство входит в состав ИПС, то повышается не только рентабельность, но и возникают эффекты: эмерджентности и синергии для этой системы.

Область квазиоптимальности показывает ещё и эффективность работы сахарного завода, то есть возможность оценить управленческие возможность (способности) администрации завода по окончанию сахарного года.

Площадь фигуры АВС находится через формулу Ньютона — Лейбница, она равна S_АВС = 1 362 064 910.

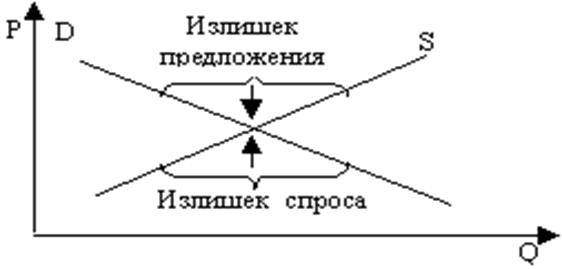
Рис. 10 Область значений спроса и предложения

По сути, весь год идет конкурентная борьба между покупателем и продавцом (производителем). Точки изображенные на рис. 9 показывают переход из одной области в другую игроками на рынка. Область DE показывает стагнацию в отношениях купли-продажи. Область EA демонстрирует активность покупателей. Область ABC продолжает показывать гиперактивность покупателей, как уже выше говорилось, происходит излишек спроса. А вот область CF наоборот представляет активную деятельность продавцов (см. табл. 1 и рис.11).

Таблица 1.

Результаты по каждой области объёма продаж сахара.

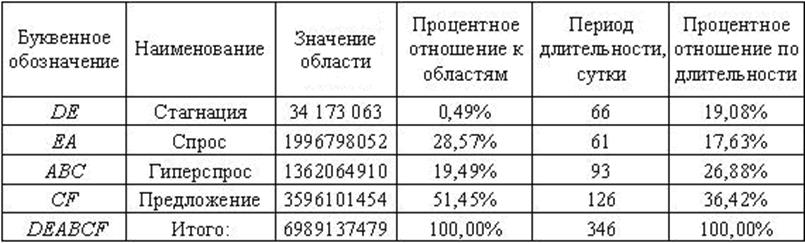
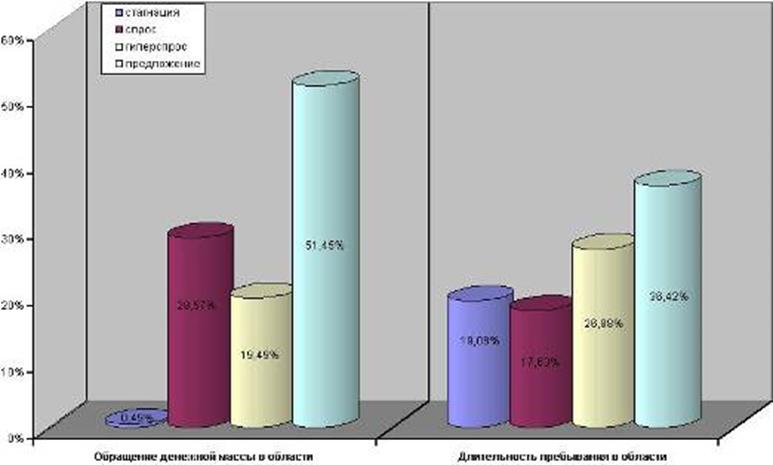
Рис. 11 Диаграмма результативности по областям

Из таблицы 1 видно, что производители в денежном эквиваленте несут потери больше, чем покупатель. А вот, по времени покупатель тратит его больше.

Данный рис. 9 явно и косвенно показывает реальное положение дел не только на отдельном сахарном заводе, но и в сахарной подотрасли Краснодарского края, и сахарной индустрии Российской Федерации в целом, так как является первоначальной единицей всей системы. Или тем самым кирпичиком фундамента, из которого состоит сахарная подотрасль, то есть, являя собой аналогию для всего комплекса в целом.

Вывод

• 1. Предложена методика обработки статистических данных сахарной подотрасли.
• 2. В результате анализа определена квазиоптимальная область эффективности сахарного завода, заключённая в пространстве пересечений: спроса, предложения и объёма продаж.
• 3. Полученные результаты могут быть использованы:
  • — при покупке/продаже сахарного завода можно определять упущенную/полученную выгоду через область квазиоптимальности, то есть возможность определения потенциала производственных мощностей завода по средствам денежного эквивалента.
  • — при определении налоговой нагрузки по сахарной отрасли через область квазиоптимальности для налоговых служб.
• 4. Возможность использовать предложенную методику в других отраслях народного хозяйства.

• 1. Захаров М. Н. Контроль и минимизация затрат предприятия в системе логистики: учебное пособие / под ред. А. А. Колобова. М.: «Экзамен», 2006. 158, [2] с.
• 2. Лойко В. И. Информационные системы и технологии в экономике. Учебник / Т. П. Барановская, В. И. Лойко, М. И. Семенов, А. И Трубилин. М.: Финансы и статистика, 2003. 416 с.: ил.
• 3. Лойко В. И. Потоковые и инвестиционно-ресурсные модели управления агропромышленным комплексом: монография / Т. П. Барановская, В. И Лойко., А. И. Трубилин. Краснодар: КубГАУ, 2006. 352 с.